Convexoid operator
Encyclopedia
In mathematics
, especially operator theory
, a convexoid operator is a bounded
linear operator T on a complex Hilbert space
H such that the closure of the numerical range
coincides with the convex hull
of its spectrum.
An example of such an operator is a normal operator
(or some of its generalization).
A closely related operator is a spectraloid operator: an operator whose spectral radius
coincides with its numerical radius. In fact, an operator T is convexoid if and only if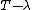
is spectraloid for every complex number 
.
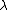Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially operator theory
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, a convexoid operator is a bounded
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
linear operator T on a complex Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H such that the closure of the numerical range
Numerical range
In the mathematical field of linear algebra and convex analysis, the numerical range of a square matrix with complex entries is a subset of the complex plane associated to the matrix...
coincides with the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of its spectrum.
An example of such an operator is a normal operator
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
(or some of its generalization).
A closely related operator is a spectraloid operator: an operator whose spectral radius
Spectral radius
In mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
coincides with its numerical radius. In fact, an operator T is convexoid if and only if
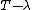is spectraloid for every complex number .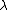