Numerical range
Encyclopedia
In the mathematical
field of linear algebra
and convex analysis
, the numerical range of a square matrix with complex entries is a subset of the complex plane
associated to the matrix. If A is an n × n matrix with complex entries, then the numerical range of A is the set
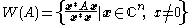
where x* denotes the Hermitian adjoint
of the vector x. In other words, it is the range of the Rayleigh quotient. The numerical range is also called the field of values.
, the numerical radius of an operator T on a complex Hilbert space, denoted by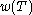
, is defined by
.
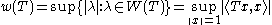w is then a norm
. It is equivalent to the operator norm by the inequality: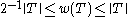
Paul Halmos
conjectured: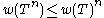
for every integer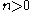
. It was later confirmed by Charles Berger and Carl Pearcy.
. Furthermore, the spectrum
of A is contained within the closure of W(A). If A is a normal matrix
, then the numerical range is the polygon
in the complex plane whose vertices are eigenvalues of A. In particular, if A is Hermitian
then the polygon reduces to the segment of the real axis bounded by the smallest and the largest eigenvalue,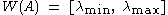
which explains the name numerical range. If A is not normal, then a weaker property holds: any "corner" of the numerical range is an eigenvalue of A. Here, the precise definition of a "corner" is that of a sharp point: a point w on the boundary
of a set S ⊂ C is called a sharp point of S if there exist two angles θ1 and θ2 with 0 ≤ θ1 < θ2 < 2π such that for all z ∈ S and for all θ ∈ (θ1, θ2) the inequality Re eiθw ≥ Re eiθz holds.
. An example of such an operator is a normal operator
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
and convex analysis
Convex analysis
Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory....
, the numerical range of a square matrix with complex entries is a subset of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
associated to the matrix. If A is an n × n matrix with complex entries, then the numerical range of A is the set
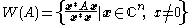
where x* denotes the Hermitian adjoint
Hermitian adjoint
In mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator.Adjoints of operators generalize conjugate transposes of square matrices to infinite-dimensional situations...
of the vector x. In other words, it is the range of the Rayleigh quotient. The numerical range is also called the field of values.
Numerical radius
In a way analogous to spectral radiusSpectral radius
In mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
, the numerical radius of an operator T on a complex Hilbert space, denoted by
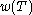, is defined by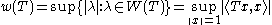.w is then a norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
. It is equivalent to the operator norm by the inequality:
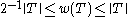
Paul Halmos
Paul Halmos
Paul Richard Halmos was a Hungarian-born American mathematician who made fundamental advances in the areas of probability theory, statistics, operator theory, ergodic theory, and functional analysis . He was also recognized as a great mathematical expositor.-Career:Halmos obtained his B.A...
conjectured:
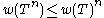
for every integer
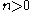. It was later confirmed by Charles Berger and Carl Pearcy.Some theorems
The Hausdorff–Toeplitz theorem states that the numerical range of any matrix is a convex setConvex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
. Furthermore, the spectrum
Spectrum of a matrix
In mathematics, the spectrum of a matrix is the set of its eigenvalues. This notion can be extended to the spectrum of an operator in the infinite-dimensional case.The determinant equals the product of the eigenvalues...
of A is contained within the closure of W(A). If A is a normal matrix
Normal matrix
A complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
, then the numerical range is the polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
in the complex plane whose vertices are eigenvalues of A. In particular, if A is Hermitian
Hermitian
A number of mathematical entities are named Hermitian, after the mathematician Charles Hermite:*Hermitian adjoint*Hermitian connection, the unique connection on a Hermitian manifold that satisfies specific conditions...
then the polygon reduces to the segment of the real axis bounded by the smallest and the largest eigenvalue,
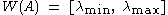
which explains the name numerical range. If A is not normal, then a weaker property holds: any "corner" of the numerical range is an eigenvalue of A. Here, the precise definition of a "corner" is that of a sharp point: a point w on the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of a set S ⊂ C is called a sharp point of S if there exist two angles θ1 and θ2 with 0 ≤ θ1 < θ2 < 2π such that for all z ∈ S and for all θ ∈ (θ1, θ2) the inequality Re eiθw ≥ Re eiθz holds.
Bounded operators on a Hilbert space
If the closure of the numerical range of a bounded operator coincides with the convex hull of its spectrum, then it is called a convexoid operatorConvexoid operator
In mathematics, especially operator theory, a convexoid operator is a bounded linear operator T on a complex Hilbert space H such that the closure of the numerical range coincides with the convex hull of its spectrum....
. An example of such an operator is a normal operator
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
.
Special cases
- matrices of order N=2. Numerical range of any operator A of order two forms an elliptical disk in the complex plane with both eigenvalues
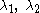as foci and minor axis equal to 
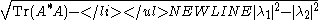. In the special case of a normal A the disk reduces to an interval, 
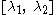- see Li 1996.
- matrices of order N=3. Numerical range forms a) an ellipse; b) has an ovular shape; c) has a flat portion of its boundary; d) is a convex hull of a point and an ellipse e) is a triangle (for normal operators only) - see Keeler, Rodman and Spitkovsky 1997.
Generalisations
- C - numerical range
- Higher rank numerical range
- Joint numerical range
- Product numerical range