
Covariance operator
Encyclopedia
in probability theory
, for a probability measure
P on a Hilbert space
H with inner product , the covariance of P is the bilinear form Cov: H × H → R given by
, the covariance of P is the bilinear form Cov: H × H → R given by
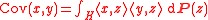
for all x and y in H. The covariance operator C is then defined by
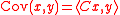
(from the Riesz representation theorem
, such operator exists if Cov is bounded). Since Cov is symmetric in its arguments, the covariance operator is
self-adjoint
(the infinite-dimensional analogy of the transposition symmetry in the finite-dimensional case). When P is a centred Gaussian measure
, C is also a nuclear operator
. In particular, it is a compact operator
of trace class
, that is, it has finite trace.
Even more generally, for a probability measure
P on a Banach space
B, the covariance of P is the bilinear form on the algebraic dual B#, defined by
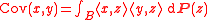
where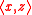 is now the value of the linear functional x on the element z.
is now the value of the linear functional x on the element z.
Quite similarly, the covariance function
of a function-valued random element
(in special cases called random process or random field
) z is
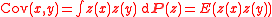
where z(x) is now the value of the function z at the point x, i.e., the value of the linear functional
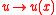 evaluated at z.
evaluated at z.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, for a probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
P on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H with inner product
 , the covariance of P is the bilinear form Cov: H × H → R given by
, the covariance of P is the bilinear form Cov: H × H → R given by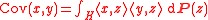
for all x and y in H. The covariance operator C is then defined by
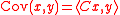
(from the Riesz representation theorem
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
, such operator exists if Cov is bounded). Since Cov is symmetric in its arguments, the covariance operator is
self-adjoint
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
(the infinite-dimensional analogy of the transposition symmetry in the finite-dimensional case). When P is a centred Gaussian measure
Gaussian measure
In mathematics, Gaussian measure is a Borel measure on finite-dimensional Euclidean space Rn, closely related to the normal distribution in statistics. There is also a generalization to infinite-dimensional spaces...
, C is also a nuclear operator
Nuclear operator
In mathematics, a nuclear operator is roughly a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis .Nuclear operators are essentially the same as trace class operators, though most authors reserve the term "trace...
. In particular, it is a compact operator
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
of trace class
Trace class
In mathematics, a trace class operator is a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis....
, that is, it has finite trace.
Even more generally, for a probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
P on a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
B, the covariance of P is the bilinear form on the algebraic dual B#, defined by
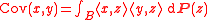
where
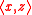 is now the value of the linear functional x on the element z.
is now the value of the linear functional x on the element z.Quite similarly, the covariance function
Covariance function
In probability theory and statistics, covariance is a measure of how much two variables change together and the covariance function describes the variance of a random variable process or field...
of a function-valued random element
Random element
In probability theory, random element is a generalization of the concept of random variable to more complicated spaces than the simple real line...
(in special cases called random process or random field
Random field
A random field is a generalization of a stochastic process such that the underlying parameter need no longer be a simple real or integer valued "time", but can instead take values that are multidimensional vectors, or points on some manifold....
) z is
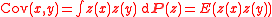
where z(x) is now the value of the function z at the point x, i.e., the value of the linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
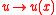 evaluated at z.
evaluated at z.

