
Covariance function
Encyclopedia
In probability theory and statistics, covariance
is a measure of how much two variables change together and the covariance function describes the variance of a random variable process or field. For a random field
or stochastic process
Z(x) on a domain D, a covariance function C(x, y) gives the covariance
of the values of the random field at the two locations x and y:

The same C(x, y) is called autocovariance
in two instances: in time series
(to denote exactly the same concept, where x is time), and in multivariate random fields (to refer to the covariance of a variable with itself, as opposed to the cross covariance
between two different variables at different locations, Cov(Z(x1), Y(x2))).
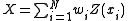
can be computed as
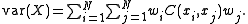
A function is a valid covariance function if and only if this variance is non-negative for all possible choices of N and weights w1, …, wN. A function with this property is called positive definite.
random field
, where
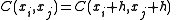
for any lag h, the covariance function can be represented by a one-parameter function

which is called a covariogram and also a covariance function. Implicitly the C(xi, xj) can be computed from Cs(h) by:
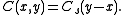
The positive definiteness
of this single-argument version of the covariance function can be checked by Bochner's theorem
.

where V is a scaling parameter, and d=d(x,y) is the distance between two points. Sample paths of a Gaussian process
with the exponential covariance function are not smooth. The "squared exponential covariance function"
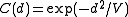
is a stationary covariance function with smooth sample paths.
The Matérn covariance function
and rational quadratic covariance function
are two parametric families of stationary covariance functions. The Matérn family includes the exponential and squared exponential covariance functions as special cases.
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
is a measure of how much two variables change together and the covariance function describes the variance of a random variable process or field. For a random field
Random field
A random field is a generalization of a stochastic process such that the underlying parameter need no longer be a simple real or integer valued "time", but can instead take values that are multidimensional vectors, or points on some manifold....
or stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
Z(x) on a domain D, a covariance function C(x, y) gives the covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
of the values of the random field at the two locations x and y:

The same C(x, y) is called autocovariance
Autocovariance
In statistics, given a real stochastic process X, the autocovariance is the covariance of the variable with itself, i.e. the variance of the variable against a time-shifted version of itself...
in two instances: in time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
(to denote exactly the same concept, where x is time), and in multivariate random fields (to refer to the covariance of a variable with itself, as opposed to the cross covariance
Cross covariance
In statistics, the term cross-covariance is sometimes used to refer to the covariance cov between two random vectors X and Y, in order to distinguish that concept from the "covariance" of a random vector X, which is understood to be the matrix of covariances between the scalar components of X.In...
between two different variables at different locations, Cov(Z(x1), Y(x2))).
Admissibility
For locations x1, x2, …, xN ∈ D the variance of every linear combination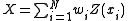
can be computed as
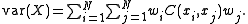
A function is a valid covariance function if and only if this variance is non-negative for all possible choices of N and weights w1, …, wN. A function with this property is called positive definite.
Simplifications with stationarity
In case of a weakly stationaryStationary process
In the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
random field
Random field
A random field is a generalization of a stochastic process such that the underlying parameter need no longer be a simple real or integer valued "time", but can instead take values that are multidimensional vectors, or points on some manifold....
, where
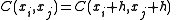
for any lag h, the covariance function can be represented by a one-parameter function

which is called a covariogram and also a covariance function. Implicitly the C(xi, xj) can be computed from Cs(h) by:
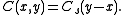
The positive definiteness
Positive definiteness
Positive definiteness is a property of the following mathematical objects:* Positive-definite bilinear form* Positive-definite matrix* Positive-definite function* Positive-definite kernel* Positive-definite function on a group...
of this single-argument version of the covariance function can be checked by Bochner's theorem
Bochner's theorem
In mathematics, Bochner's theorem characterizes the Fourier transform of a positive finite Borel measure on the real line.- Background :...
.
Parametric families of covariance functions
A simple stationary parametric covariance function is the "exponential covariance function"
where V is a scaling parameter, and d=d(x,y) is the distance between two points. Sample paths of a Gaussian process
Gaussian process
In probability theory and statistics, a Gaussian process is a stochastic process whose realisations consist of random values associated with every point in a range of times such that each such random variable has a normal distribution...
with the exponential covariance function are not smooth. The "squared exponential covariance function"
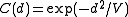
is a stationary covariance function with smooth sample paths.
The Matérn covariance function
Matérn covariance function
In statistics, the Matérn covariance is a covariance function used in spatial statistics, geostatistics, machine learning, image analysis, and other applications of multivariate statistical analysis on metric spaces...
and rational quadratic covariance function
Rational quadratic covariance function
In statistics, the rational quadratic covariance function is used in spatial statistics, geostatistics, machine learning, image analysis, and other fields where multivariate statistical analysis is conducted on metric spaces. It is commonly used to define the statistical covariance between...
are two parametric families of stationary covariance functions. The Matérn family includes the exponential and squared exponential covariance functions as special cases.
See also
- VariogramVariogramIn spatial statistics the theoretical variogram 2\gamma is a function describing the degree of spatial dependence of a spatial random field or stochastic process Z...
- Random fieldRandom fieldA random field is a generalization of a stochastic process such that the underlying parameter need no longer be a simple real or integer valued "time", but can instead take values that are multidimensional vectors, or points on some manifold....
- Stochastic processStochastic processIn probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
- KrigingKrigingKriging is a group of geostatistical techniques to interpolate the value of a random field at an unobserved location from observations of its value at nearby locations....
- Autocorrelation function
- Correlation functionCorrelation functionA correlation function is the correlation between random variables at two different points in space or time, usually as a function of the spatial or temporal distance between the points...

