Cross-entropy method
Encyclopedia
The cross-entropy method attributed to Reuven Rubinstein is a general Monte Carlo
approach to
combinatorial
and continuous
multi-extremal optimization
and importance sampling
.
The method originated from the field of rare event simulation, where
very small probabilities need to be accurately estimated, for example in network reliability analysis, queueing models, or performance analysis of telecommunication systems.
The CE method can be applied to static and noisy combinatorial optimization problems such as the traveling salesman problem, the quadratic assignment problem
, DNA sequence alignment
, the max-cut problem and the buffer allocation problem, as well as continuous global optimization
problems with many local extrema.
In a nutshell the CE method consists of two phases:
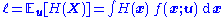, where 
is some performance function and 
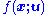is a member of some parametric family
of distributions. Using importance sampling
this quantity can be estimated as
, where 
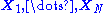is a random sample from 
. For positive 
, the theoretically optimal importance sampling density
(pdf)is given by
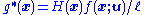. This, however, depends on the unknown 
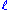. The CE method aims to approximate the optimal pdf by adaptively selecting members of the parametric family that are closest (in the Kullback-Leibler sense) to the optimal pdf 
.
In several cases, the solution to step 3 can be found analytically. Situations in which this occurs are
Suppose the problem is to maximize some function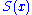
, for example,
.
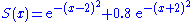To apply CE, one considers first the associated stochastic problem of estimating
for a given level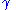
, and parametric family 
, for example the 1-dimensional
Gaussian distribution,
parameterized by its mean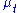
and variance 
(so 
here).
Hence, for a given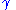
, the goal is to find 
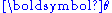so that
is minimized. This is done by solving the sample version (stochastic counterpart) of the KL divergence minimization problem, as in step 3 above.
It turns out that parameters that minimize the stochastic counterpart for this choice of target distribution and
parametric family are the sample mean and sample variance corresponding to the elite samples, which are those samples that have objective function value
.
The worst of the elite samples is then used as the level parameter for the next iteration.
This yields the following randomized algorithm that happens to coincide with the so-called Estimation of Multivariate Normal Algorithm (EMNA), an estimation of distribution algorithm.
2. N:=100; Ne:=10; //
3. while t < maxits and sigma2 > epsilon // While not converged and maxits not exceeded
4. X = SampleGaussian(mu,sigma2,N); // Obtain N samples from current sampling distribution
5. S = exp(-(X-2)^2) + 0.8 exp(-(X+2)^2); // Evaluate objective function at sampled points
6. X = sort(X,S); // Sort X by objective function values (in descending order)
7. mu = mean(X(1:Ne)); sigma2=var(X(1:Ne)); // Update parameters of sampling distribution
8. t = t+1; // Increment iteration counter
9. return mu // Return mean of final sampling distribution as solution
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
approach to
combinatorial
Combinatorial optimization
In applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not feasible...
and continuous
Continuous optimization
Continuous optimization is a branch of optimization in applied mathematics.As opposed to discrete optimization, the variables used in the objective function can assume real values, e.g., values from intervals of the real line....
multi-extremal optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
and importance sampling
Importance sampling
In statistics, importance sampling is a general technique for estimating properties of a particular distribution, while only having samples generated from a different distribution rather than the distribution of interest. It is related to Umbrella sampling in computational physics...
.
The method originated from the field of rare event simulation, where
very small probabilities need to be accurately estimated, for example in network reliability analysis, queueing models, or performance analysis of telecommunication systems.
The CE method can be applied to static and noisy combinatorial optimization problems such as the traveling salesman problem, the quadratic assignment problem
Quadratic assignment problem
The quadratic assignment problem is one of fundamental combinatorial optimization problems in the branch of optimization or operations research in mathematics, from the category of the facilities location problems....
, DNA sequence alignment
Sequence alignment
In bioinformatics, a sequence alignment is a way of arranging the sequences of DNA, RNA, or protein to identify regions of similarity that may be a consequence of functional, structural, or evolutionary relationships between the sequences. Aligned sequences of nucleotide or amino acid residues are...
, the max-cut problem and the buffer allocation problem, as well as continuous global optimization
Global optimization
Global optimization is a branch of applied mathematics and numerical analysis that deals with the optimization of a function or a set of functions to some criteria.- General :The most common form is the minimization of one real-valued function...
problems with many local extrema.
In a nutshell the CE method consists of two phases:
- Generate a random data sample (trajectories, vectors, etc.) according to a specified mechanism.
- Update the parameters of the random mechanism based on the data to produce a "better" sample in the next iteration. This step involves minimizing the cross-entropyCross entropyIn information theory, the cross entropy between two probability distributions measures the average number of bits needed to identify an event from a set of possibilities, if a coding scheme is used based on a given probability distribution q, rather than the "true" distribution p.The cross entropy...
or Kullback-Leibler divergence.
Estimation via importance sampling
Consider the general problem of estimating the quantity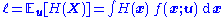, where is some performance function and 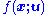is a member of some parametric familyParametric family
In mathematics and its applications, a parametric family or a parameterized family is a family of objects whose definitions depend on a set of parameters....
of distributions. Using importance sampling
Importance sampling
In statistics, importance sampling is a general technique for estimating properties of a particular distribution, while only having samples generated from a different distribution rather than the distribution of interest. It is related to Umbrella sampling in computational physics...
this quantity can be estimated as
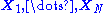, where is a random sample from . For positive , the theoretically optimal importance sampling densityProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
(pdf)is given by
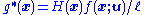. This, however, depends on the unknown 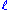. The CE method aims to approximate the optimal pdf by adaptively selecting members of the parametric family that are closest (in the Kullback-Leibler sense) to the optimal pdf .Generic CE algorithm
- Choose initial parameter vector
; set t = 1. - Generate a random sample
from 
- Solve for
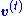, where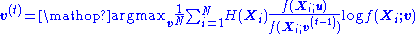
- If convergence is reached then stop; otherwise, increase t by 1 and reiterate from step 2.
In several cases, the solution to step 3 can be found analytically. Situations in which this occurs are
- When
belongs to the natural exponential familyExponential familyIn probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential... - When
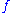is discreteDiscrete spaceIn topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
with finite supportSupport (mathematics)In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis... - When
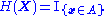and 
, then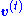 
corresponds to the maximum likelihood estimatorMaximum likelihoodIn statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
based on those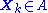
.
Continuous optimization—example
The same CE algorithm can be used for optimization, rather than estimation.Suppose the problem is to maximize some function
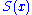, for example,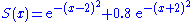.To apply CE, one considers first the associated stochastic problem of estimating
for a given level
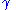, and parametric family , for example the 1-dimensionalGaussian distribution,
parameterized by its mean
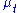and variance (so here).Hence, for a given
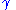, the goal is to find 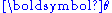so thatis minimized. This is done by solving the sample version (stochastic counterpart) of the KL divergence minimization problem, as in step 3 above.
It turns out that parameters that minimize the stochastic counterpart for this choice of target distribution and
parametric family are the sample mean and sample variance corresponding to the elite samples, which are those samples that have objective function value
.The worst of the elite samples is then used as the level parameter for the next iteration.
This yields the following randomized algorithm that happens to coincide with the so-called Estimation of Multivariate Normal Algorithm (EMNA), an estimation of distribution algorithm.
Pseudo-code
1. mu:=-6; sigma2:=100; t:=0; maxits=100; // Initialize parameters2. N:=100; Ne:=10; //
3. while t < maxits and sigma2 > epsilon // While not converged and maxits not exceeded
4. X = SampleGaussian(mu,sigma2,N); // Obtain N samples from current sampling distribution
5. S = exp(-(X-2)^2) + 0.8 exp(-(X+2)^2); // Evaluate objective function at sampled points
6. X = sort(X,S); // Sort X by objective function values (in descending order)
7. mu = mean(X(1:Ne)); sigma2=var(X(1:Ne)); // Update parameters of sampling distribution
8. t = t+1; // Increment iteration counter
9. return mu // Return mean of final sampling distribution as solution
Related methods
- Simulated annealingSimulated annealingSimulated annealing is a generic probabilistic metaheuristic for the global optimization problem of locating a good approximation to the global optimum of a given function in a large search space. It is often used when the search space is discrete...
- Genetic algorithms
- Harmony searchHarmony searchIn computer science and operations research, harmony search is a phenomenon-mimicking algorithm inspired by the improvisation process of musicians...
- Estimation of distribution algorithm
- Tabu searchTabu searchTabu search is a mathematical optimization method, belonging to the class of trajectory based techniques. Tabu search enhances the performance of a local search method by using memory structures that describe the visited solutions: once a potential solution has been determined, it is marked as...
See also
- Cross entropyCross entropyIn information theory, the cross entropy between two probability distributions measures the average number of bits needed to identify an event from a set of possibilities, if a coding scheme is used based on a given probability distribution q, rather than the "true" distribution p.The cross entropy...
- Kullback-Leibler divergence
- Randomized algorithmRandomized algorithmA randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
- Importance samplingImportance samplingIn statistics, importance sampling is a general technique for estimating properties of a particular distribution, while only having samples generated from a different distribution rather than the distribution of interest. It is related to Umbrella sampling in computational physics...