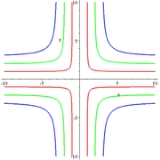
Cruciform curve
Encyclopedia
The cruciform curve, or cross curve is a quartic plane curve
given by the equation
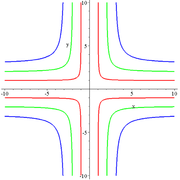
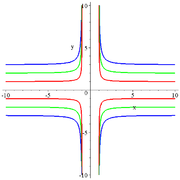
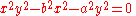
where a and b are two parameter
s determining the shape of the curve.
The cruciform curve is related by a standard quadratic transformation, x ↦ 1/x, y ↦ 1/y to the ellipse a2x2 + b2y2 = 1, and is therefore a rational plane algebraic curve
of genus
zero. The cruciform curve has three double points in the real projective plane
, at x=0 and y=0, x=0 and z=0, and y=0 and z=0.
Because the curve is rational, it can be parametrized by rational functions. For instance, if a=1 and b=2, then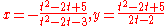
parametrizes the points on the curve outside of the exceptional cases where the denominator is zero.
Quartic plane curve
A quartic plane curve is a plane curve of the fourth degree. It can be defined by a quartic equation:Ax^4+By^4+Cx^3y+Dx^2y^2+Exy^3+Fx^3+Gy^3+Hx^2y+Ixy^2+Jx^2+Ky^2+Lxy+Mx+Ny+P=0....
given by the equation


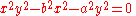
where a and b are two parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
s determining the shape of the curve.
The cruciform curve is related by a standard quadratic transformation, x ↦ 1/x, y ↦ 1/y to the ellipse a2x2 + b2y2 = 1, and is therefore a rational plane algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
of genus
Geometric genus
In algebraic geometry, the geometric genus is a basic birational invariant pg of algebraic varieties and complex manifolds.-Definition:...
zero. The cruciform curve has three double points in the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
, at x=0 and y=0, x=0 and z=0, and y=0 and z=0.
Because the curve is rational, it can be parametrized by rational functions. For instance, if a=1 and b=2, then
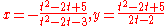
parametrizes the points on the curve outside of the exceptional cases where the denominator is zero.

