Curvature collineation
Encyclopedia
A curvature collineation (often abbreviated to CC) is vector field
which preserves the Riemann tensor in the sense that,
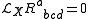
where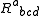
are the components of the Riemann tensor. The set of all smooth
curvature collineations forms a Lie algebra
under the Lie bracket
operation (if the smoothness condition is dropped, the set of all curvature collineations need not form a Lie algebra). The Lie algebra is denoted by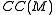
and may be infinite
-dimension
al. Every affine vector field
is a curvature collineation.
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
which preserves the Riemann tensor in the sense that,
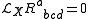
where
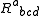are the components of the Riemann tensor. The set of all smoothSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
curvature collineations forms a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
under the Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
operation (if the smoothness condition is dropped, the set of all curvature collineations need not form a Lie algebra). The Lie algebra is denoted by
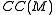and may be infiniteInfinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al. Every affine vector field
Affine vector field
An affine vector field is a projective vector field preserving geodesics and preserving the affine parameter...
is a curvature collineation.
See also
- Conformal vector field
- Homothetic vector field
- Killing vector fieldKilling vector fieldIn mathematics, a Killing vector field , named after Wilhelm Killing, is a vector field on a Riemannian manifold that preserves the metric. Killing fields are the infinitesimal generators of isometries; that is, flows generated by Killing fields are continuous isometries of the manifold...
- Matter collineation
- Spacetime symmetriesSpacetime symmetriesSpacetime symmetries are features of spacetime that can be described as exhibiting some form of symmetry. The role of symmetry in physics is important in simplifying solutions to many problems, spacetime symmetries finding ample application in the study of exact solutions of Einstein's field...