
Conformal vector field
Encyclopedia
A conformal vector field (often conformal Killing vector field and occasionally conformal or conformal collineation) of a Riemannian manifold
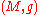 is a vector field
is a vector field
 that satisfies:
that satisfies:

for some smooth real-valued function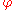 on
on  , where
, where 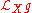 denotes the Lie derivative
denotes the Lie derivative
of the metric with respect to
with respect to  . In the case that
. In the case that 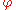 is identically zero,
is identically zero,  is called a Killing vector field
is called a Killing vector field
.
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
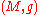 is a vector field
is a vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
 that satisfies:
that satisfies:
for some smooth real-valued function
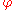 on
on  , where
, where 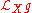 denotes the Lie derivative
denotes the Lie derivativeLie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
of the metric
 with respect to
with respect to  . In the case that
. In the case that 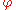 is identically zero,
is identically zero,  is called a Killing vector field
is called a Killing vector fieldKilling vector field
In mathematics, a Killing vector field , named after Wilhelm Killing, is a vector field on a Riemannian manifold that preserves the metric. Killing fields are the infinitesimal generators of isometries; that is, flows generated by Killing fields are continuous isometries of the manifold...
.
See also
- Affine vector fieldAffine vector fieldAn affine vector field is a projective vector field preserving geodesics and preserving the affine parameter...
- Curvature collineation
- Homothetic vector field
- Killing vector fieldKilling vector fieldIn mathematics, a Killing vector field , named after Wilhelm Killing, is a vector field on a Riemannian manifold that preserves the metric. Killing fields are the infinitesimal generators of isometries; that is, flows generated by Killing fields are continuous isometries of the manifold...
- Matter collineation
- Spacetime symmetriesSpacetime symmetriesSpacetime symmetries are features of spacetime that can be described as exhibiting some form of symmetry. The role of symmetry in physics is important in simplifying solutions to many problems, spacetime symmetries finding ample application in the study of exact solutions of Einstein's field...

