Cyclic prefix
Encyclopedia
In telecommunications, the term cyclic prefix refers to the prefixing of a symbol with a repetition of the end. Although the receiver is typically configured to discard the cyclic prefix samples, the cyclic prefix serves two purposes.
In order for the cyclic prefix to be effective (i.e. to serve its aforementioned objectives), the length of the cyclic prefix must be at least equal to the length of the multipath channel. Although the concept of cyclic prefix has been traditionally associated with OFDM systems, the cyclic prefix is now also used in single carrier systems to improve the robustness to multipath.
, and time-invariant systems. Therefore, if the channel is assumed to be linear
and time-invariant, then a sinusoid of infinite duration would be an eigenfunction
. However, in practice, this cannot be achieved, as real signals are always time-limited. So, to mimic the infinite behavior, prefixing the end of the symbol to the beginning makes the linear convolution
of the channel appear as though it were circular convolution
, and thus, preserve this property in the part of the symbol after the cyclic prefix.
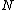subcarriers. The message symbol can be written as:
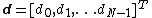
The OFDM symbol is constructed by taking the inverse discrete Fourier transform
(IDFT) of the message symbol, followed by a cyclic prefixing. Let the symbol obtained by the IDFT be denoted by
.
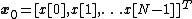Prefixing it with a cyclic prefix of length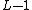
, the OFDM symbol obtained is:
.
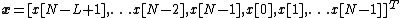Assume that the channel is represented using
.
Then, after convolution with the channel, which happens as
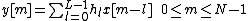
which is circular convolution, as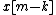
becomes 
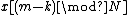. So, taking the Discrete Fourier Transform
, we get
.
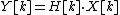where
is the discrete Fourier transform
of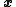
. Thus, a multipath channel is converted into scalar parallel sub-channels in frequency domain, thereby simplifying the receiver design considerably. The task of channel estimation is simplified, as we just need to estimate the scalar coefficients 
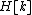for each sub-channel and once the values of 
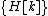are estimated, for the duration in which the channel does not vary significantly, merely multiplying the received demodulated symbols by the inverse of 
yields the estimates of 
and hence, the estimate of actual symbols 
.
- As a guard intervalGuard intervalIn telecommunications, guard intervals are used to ensure that distinct transmissions do not interfere with one another. These transmissions may belong to different users or to the same user ....
, it eliminates the intersymbol interferenceIntersymbol interferenceIn telecommunication, intersymbol interference is a form of distortion of a signal in which one symbol interferes with subsequent symbols. This is an unwanted phenomenon as the previous symbols have similar effect as noise, thus making the communication less reliable...
from the previous symbol. - As a repetition of the end of the symbol, it allows the linear convolution of a frequency-selective multipath channel to be modelled as circular convolution, which in turn may be transformed to the frequency domain using a discrete Fourier transformDiscrete Fourier transformIn mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
. This approach allows for simple frequency-domain processing, such as channel estimation and equalization.
In order for the cyclic prefix to be effective (i.e. to serve its aforementioned objectives), the length of the cyclic prefix must be at least equal to the length of the multipath channel. Although the concept of cyclic prefix has been traditionally associated with OFDM systems, the cyclic prefix is now also used in single carrier systems to improve the robustness to multipath.
Principle
Cyclic prefix is often used in conjunction with modulation in order to retain sinusoids' properties in multipath channels. It is well known that sinusoidal signals are eigenfunctions of linearLinear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
, and time-invariant systems. Therefore, if the channel is assumed to be linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
and time-invariant, then a sinusoid of infinite duration would be an eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
. However, in practice, this cannot be achieved, as real signals are always time-limited. So, to mimic the infinite behavior, prefixing the end of the symbol to the beginning makes the linear convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of the channel appear as though it were circular convolution
Circular convolution
The circular convolution, also known as cyclic convolution, of two aperiodic functions occurs when one of them is convolved in the normal way with a periodic summation of the other function. That situation arises in the context of the Circular convolution theorem...
, and thus, preserve this property in the part of the symbol after the cyclic prefix.
Use in OFDM
Cyclic Prefixes are used in OFDM in order to combat multipath by making channel estimation easy. As an example, consider an OFDM system which has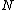 subcarriers. The message symbol can be written as: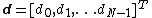The OFDM symbol is constructed by taking the inverse discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
(IDFT) of the message symbol, followed by a cyclic prefixing. Let the symbol obtained by the IDFT be denoted by
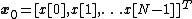.Prefixing it with a cyclic prefix of length
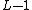, the OFDM symbol obtained is: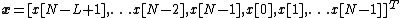.Assume that the channel is represented using
.Then, after convolution with the channel, which happens as
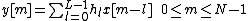
which is circular convolution, as
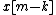becomes 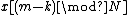. So, taking the Discrete Fourier TransformDiscrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
, we get
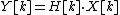.where
is the discrete Fourier transformDiscrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
of
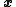. Thus, a multipath channel is converted into scalar parallel sub-channels in frequency domain, thereby simplifying the receiver design considerably. The task of channel estimation is simplified, as we just need to estimate the scalar coefficients 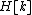for each sub-channel and once the values of 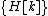are estimated, for the duration in which the channel does not vary significantly, merely multiplying the received demodulated symbols by the inverse of yields the estimates of and hence, the estimate of actual symbols .