Cylindrical equal-area projection
Encyclopedia
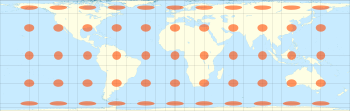
Cartography
Cartography is the study and practice of making maps. Combining science, aesthetics, and technique, cartography builds on the premise that reality can be modeled in ways that communicate spatial information effectively.The fundamental problems of traditional cartography are to:*Set the map's...
, the cylindrical equal-area projection is a family of cylindrical, equal area map projection
Map projection
A map projection is any method of representing the surface of a sphere or other three-dimensional body on a plane. Map projections are necessary for creating maps. All map projections distort the surface in some fashion...
s.
Cylindrical projections
The term "normal cylindrical projection" is used to refer to any projection in which meridiansMeridian (geography)
A meridian is an imaginary line on the Earth's surface from the North Pole to the South Pole that connects all locations along it with a given longitude. The position of a point along the meridian is given by its latitude. Each meridian is perpendicular to all circles of latitude...
are mapped to equally spaced vertical lines and circles of latitude (parallels) are mapped to horizontal lines (or, mutatis mutandis
Mutatis mutandis
Mutatis mutandis is a Latin phrase meaning "by changing those things which need to be changed" or more simply "the necessary changes having been made"....
, more generally, radial lines from a fixed point are mapped to equally spaced parallel lines and concentric circles around it are mapped to perpendicular lines).
The mapping of meridians to vertical lines can be visualized by imagining a cylinder (of which the axis coincides with the Earth's axis of rotation) wrapped around the Earth and then projecting onto the cylinder, and subsequently unfolding the cylinder.
By the geometry of their construction, cylindrical projections stretch distances east-west. The amount of stretch is the same at any chosen latitude on all cylindrical projections, and is given by the secant
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
of the latitude
Latitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
as a multiple of the equator's scale. The various cylindrical projections are distinguished from each other solely by their north-south stretching (where latitude is given by φ):
The only cylindrical projections that preserve area have a
- North-south compression precisely the reciprocal of east-west stretching (cosine φ): equal-area cylindrical (with many named specializations such as Gall–Peters or Gall orthographic, BehrmannBehrmann projectionThe Behrmann projection is a cylindrical map projection. This is an orthographic projection onto a cylinder secant at the 30° parallels. It is equal-area, but distortion of shape increases with distance from the standard parallels. Scale is true along the standard parallels and constant between two...
, and Lambert cylindrical equal-areaLambert cylindrical equal-area projectionIn cartography, the Lambert cylindrical equal-area projection, or Lambert cylindrical projection, is acylindrical, equal area map projection...
). This divides north-south distances by a factor equal to the secant of the latitude, preserving area but heavily distorting shapes.
Any particular cylindrical equal-area map has a pair of identical latitudes of opposite sign (or else the equator) at which the east-west scale matches the north-south-scale.
Formulae
All cylindrical equal-area projections use the formula: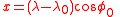
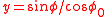
where
is the longitude, 
is the central meridian, 
is the latitude, and 
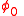is the standard latitude, all expressed in radians.Some cartographers prefer to work in degrees, rather than radians, and use the equivalent formula:
Simplified formula
Stripping out unit conversion and uniform scaling, the formulae may be written: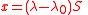
Hence the sphere is mapped onto a stretched vertical cylinder. The stretch factor S is what distinguishes the variations of cylindric equal-area projection.
Discussion
The various specializations of the cylindric equal-area projection differ only in the ratio of the vertical to horizontal axis. This ratio determines the standard parallel of the projection, which is the parallel at which there is no distortion and along which distances match the stated scale. There are always two standard parallels on the cylindric equal-area projection, each at the same distance north and south of the equator. The standard parallels of the Gall–Peters are 45° N and 45° S. Several other specializations of the equal-area cylindric have been described, promoted, or otherwise named.| Projection | Image | Creator (year) |
Standard parallels N/S | Width/height aspect ratio | Notes |
|---|---|---|---|---|---|
| cylindrical equal-area |  |
 |
Base projection for all the others. | ||
| Lambert Lambert cylindrical equal-area projection In cartography, the Lambert cylindrical equal-area projection, or Lambert cylindrical projection, is acylindrical, equal area map projection... |
|
Johann Heinrich Lambert Johann Heinrich Lambert Johann Heinrich Lambert was a Swiss mathematician, physicist, philosopher and astronomer.Asteroid 187 Lamberta was named in his honour.-Biography:... (1772) |
Equator (0°) |  |
|
| Behrmann Behrmann projection The Behrmann projection is a cylindrical map projection. This is an orthographic projection onto a cylinder secant at the 30° parallels. It is equal-area, but distortion of shape increases with distance from the standard parallels. Scale is true along the standard parallels and constant between two... |
Walter Behrmann (1910) |
30° | 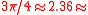  Silver ratio In mathematics, two quantities are in the silver ratio if the ratio between the sum of the smaller plus twice the larger of those quantities and the larger one is the same as the ratio between the larger one and the smaller. This defines the silver ratio as an irrational mathematical constant,... |
||
| Smyth equal-surface = Craster rectangular |
C. Piazzi Smyth (1870) |
37°04' |  |
||
| Trystan Edwards | Trystan Edwards (1953) | 37°24' |  |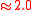
||
| Hobo–Dyer | Mick Dyer (2002) |
37°30' |  |
||
| Gall–Peters = Gall orthographic = Peters |
James Gall James Gall James Gall was a Scottish clergyman who founded the Carrubbers Close Mission. As well as writing on religious matters, often from a rather unorthodox standpoint, he had an interest in astronomy... (1855) |
45° | 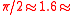 ΦGolden ratio In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989... |
Promoted by Arno Peters as a new invention in 1967. | |
| Balthasart | M. Balthasart (1935) |
50° |  |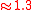
History
The invention of the Lambert cylindrical equal-area projection is attributed to the AlsatianAlsace
Alsace is the fifth-smallest of the 27 regions of France in land area , and the smallest in metropolitan France. It is also the seventh-most densely populated region in France and third most densely populated region in metropolitan France, with ca. 220 inhabitants per km²...
mathematician Johann Heinrich Lambert
Johann Heinrich Lambert
Johann Heinrich Lambert was a Swiss mathematician, physicist, philosopher and astronomer.Asteroid 187 Lamberta was named in his honour.-Biography:...
in 1772.
Arno Peters
Arno Peters
Arno Peters developed the Peters world map, based on the Gall–Peters projection.Born in Berlin, Germany, he began his career as a filmmaker who studied American techniques of filmmaking during the late 1930s, and helped to revolutionize film production in Germany at the time...
devised an equal-area map in 1967 and presented it as a "new invention in 1973."
The Tobler hyperelliptical projection
Tobler hyperelliptical projection
The Tobler hyperelliptical projection is a family of equal-area pseudocylindrical projections used for mapping the earth. It is named for Waldo R...
, first described by Tobler in 1973, is a further generalization of the cylindrical equal-area family.
The HEALPix
HEALPix
HEALPix , an acronym for Hierarchical Equal Area isoLatitude Pixelisation of a 2-sphere, can refer to either an algorithm for pixelisation of the 2-sphere, an associated software package, or an associated class of map projections.The HEALPix projection is a general class of spherical projections,...
projection is an equal-area hybrid combination of: the Lambert cylindrical equal-area projection, for the equatorial regions of the sphere; and an interrupted Collignon projection, for the polar regions.