DBSCAN
Encyclopedia
DBSCAN is a data clustering
algorithm proposed by Martin Ester, Hans-Peter Kriegel
, Jörg Sander and Xiaowei Xu in 1996.
It is a density-based clustering algorithm because it finds a number of clusters starting from the estimated density distribution of corresponding nodes. DBSCAN is one of the most common clustering algorithms and also most cited in scientific literature. OPTICS
can be seen as a generalization of DBSCAN to multiple ranges, effectively replacing the
parameter with a maximum search radius.
is directly density-reachable from a point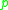 
if it is not farther away than a given distance 
(i.e., is part of its 
-neighborhood), and if 
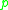is surrounded by sufficiently many points such that one may consider 
and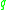 
be part of a cluster. 
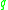is called density-reachable (note: this is different from "directly density-reachable") from 
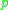if there is a sequence 
of points with 
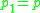and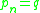 
where each 
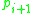is directly density-reachable from 
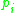. Note that the relation of density-reachable is not symmetric (since 
might lie on the edge of a cluster, having insufficiently many neighbors to count as a genuine cluster element), so the notion of density-connected is introduced: two points 
and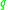 
are density-connected if there is a point 
such that
both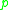
and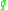 
are density reachable from 
.
A cluster, which is a subset of the points of the database, satisfies two properties:
(eps) and the minimum number of points required to form a cluster (minPts). It starts with an arbitrary starting point that has not been visited. This point's 
-neighborhood is retrieved, and if it contains sufficiently many points, a cluster is started. Otherwise, the point is labeled as noise. Note that this point might later be found in a sufficiently sized 
-environment of a different point and hence be made part of a cluster.
If a point is found to be part of a cluster, its
-neighborhood is also part of that cluster. Hence, all points that are found within the 
-neighborhood are added, as is their own 
-neighborhood. This process continues until the cluster is completely found. Then, a new unvisited point is retrieved and processed, leading to the discovery of a further cluster or noise.
C = 0
for each unvisited point P in dataset D
mark P as visited
N = regionQuery(P, eps)
if sizeof(N) < MinPts
mark P as NOISE
else
C = next cluster
expandCluster(P, N, C, eps, MinPts)
expandCluster(P, N, C, eps, MinPts)
add P to cluster C
for each point P' in N
if P' is not visited
mark P' as visited
N' = regionQuery(P', eps)
if sizeof(N') >= MinPts
N = N joined with N'
if P' is not yet member of any cluster
add P' to cluster C
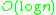, an overall runtime complexity of 
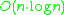is obtained. Without the use of an accelerating index structure, the run time complexity is 
. Often the distance matrix of size 
is materialized to avoid distance recomputations. This however also needs 
memory.
See the section on extensions below for algorithmic modifications to handle these issues.
and MinPts are needed. The parameters must be specified by the user of the algorithms since other data sets and other questions require different parameters. An initial value for 
can be determined by a k-distance graph. As a rule of thumb,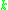 
can be derived from the number of dimensions in the data set 
as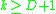 
. However, larger values are usually better for data sets with noise.
Although this parameter estimation gives a sufficient initial parameter set the resulting clustering can turn out to be not the expected partitioning. Therefore research has been performed on incrementally optimizing the parameters against a specific target value.
OPTICS
can be seen as a generalization of DBSCAN that replaces the
parameter with a maximum value that mostly effects performance. MinPts then essentially becomes the minimum cluster size to find. While the algorithm is a lot easier to parameterize than DBSCAN, the results are a bit more difficult to use, as it will usually produce a hierarchical clustering instead of the simple data partitioning that DBSCAN produces.
and minpts parameters are removed from the original algorithm and moved to the predicates. For example on polygon data, the "neighborhood" could be any intersecting polygon, whereas the density predicate uses the polygon areas instead of just the object count.
presented by Dirk Habich and Peter Benjamin Volk. The basic idea has been extended to hierarchical clustering by the OPTICS algorithm
. DBSCAN is also used as part of subspace clustering algorithms like PreDeCon and SUBCLU
.
Data clustering
Cluster analysis or clustering is the task of assigning a set of objects into groups so that the objects in the same cluster are more similar to each other than to those in other clusters....
algorithm proposed by Martin Ester, Hans-Peter Kriegel
Hans-Peter Kriegel
Hans-Peter Kriegel is a German computer scientist and professor at the Ludwig Maximilian University of Munich and leading the Database Systems Group in the Department of Computer Science....
, Jörg Sander and Xiaowei Xu in 1996.
It is a density-based clustering algorithm because it finds a number of clusters starting from the estimated density distribution of corresponding nodes. DBSCAN is one of the most common clustering algorithms and also most cited in scientific literature. OPTICS
OPTICS algorithm
OPTICS is an algorithm for finding density-based clusters in spatial data. It was presented by Mihael Ankerst, Markus M. Breunig, Hans-Peter Kriegel and Jörg Sander....
can be seen as a generalization of DBSCAN to multiple ranges, effectively replacing the
parameter with a maximum search radius.Basic idea
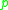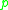DBSCAN's definition of a cluster is based on the notion of density reachability. Basically, a point is directly density-reachable from a point if it is not farther away than a given distance (i.e., is part of its -neighborhood), and if is surrounded by sufficiently many points such that one may consider and 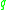be part of a cluster. 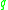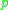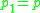is called density-reachable (note: this is different from "directly density-reachable") from if there is a sequence of points with and 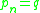where each 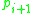is directly density-reachable from 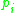. Note that the relation of density-reachable is not symmetric (since might lie on the edge of a cluster, having insufficiently many neighbors to count as a genuine cluster element), so the notion of density-connected is introduced: two points and 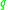are density-connected if there is a point such thatboth
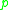and 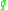are density reachable from .A cluster, which is a subset of the points of the database, satisfies two properties:
- All points within the cluster are mutually density-connected.
- If a point is density-connected to any point of the cluster, it is part of the cluster as well.
Algorithm
DBSCAN requires two parameters: (eps) and the minimum number of points required to form a cluster (minPts). It starts with an arbitrary starting point that has not been visited. This point's -neighborhood is retrieved, and if it contains sufficiently many points, a cluster is started. Otherwise, the point is labeled as noise. Note that this point might later be found in a sufficiently sized -environment of a different point and hence be made part of a cluster.If a point is found to be part of a cluster, its
-neighborhood is also part of that cluster. Hence, all points that are found within the -neighborhood are added, as is their own -neighborhood. This process continues until the cluster is completely found. Then, a new unvisited point is retrieved and processed, leading to the discovery of a further cluster or noise.Pseudocode
DBSCAN(D, eps, MinPts)C = 0
for each unvisited point P in dataset D
mark P as visited
N = regionQuery(P, eps)
if sizeof(N) < MinPts
mark P as NOISE
else
C = next cluster
expandCluster(P, N, C, eps, MinPts)
expandCluster(P, N, C, eps, MinPts)
add P to cluster C
for each point P' in N
if P' is not visited
mark P' as visited
N' = regionQuery(P', eps)
if sizeof(N') >= MinPts
N = N joined with N'
if P' is not yet member of any cluster
add P' to cluster C
Complexity
DBSCAN visits each point of the database, possibly multiple times (e.g., as candidates to different clusters). For practical considerations, however, the time complexity is mostly governed by the number of regionQuery invocations. DBSCAN executes exactly one such query for each point, and if an indexing structure is used that executes such a neighborhood query in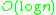, an overall runtime complexity of 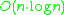is obtained. Without the use of an accelerating index structure, the run time complexity is . Often the distance matrix of size is materialized to avoid distance recomputations. This however also needs memory.Advantages
- DBSCAN does not require you to know the number of clusters in the data a priori, as opposed to k-meansK-means algorithmIn statistics and data mining, k-means clustering is a method of cluster analysis which aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean...
. - DBSCAN can find arbitrarily shaped clusters. It can even find clusters completely surrounded by (but not connected to) a different cluster. Due to the MinPts parameter, the so-called single-link effect (different clusters being connected by a thin line of points) is reduced.
- DBSCAN has a notion of noise.
- DBSCAN requires just two parameters and is mostly insensitive to the ordering of the points in the database. (Only points sitting on the edge of two different clusters might swap cluster membership if the ordering of the points is changed, and the cluster assignment is unique only up to isomorphism.)
Disadvantages
- DBSCAN can only result in a good clustering as good as its distance measureMetric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
is in the function regionQuery(P,
). The most common distance metric used is the euclidean distanceEuclidean distanceIn mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
measure. Especially for high-dimensional dataClustering high-dimensional dataClustering high-dimensional data is the cluster analysis of data with anywhere from a few dozen to many thousands of dimensions. Such high-dimensional data spaces are often encountered in areas such as medicine, where DNA microarray technology can produce a large number of measurements at once, and...
, this distance metric can be rendered almost useless due to the so called "Curse of dimensionalityCurse of dimensionalityThe curse of dimensionality refers to various phenomena that arise when analyzing and organizing high-dimensional spaces that do not occur in low-dimensional settings such as the physical space commonly modeled with just three dimensions.There are multiple phenomena referred to by this name in...
", rendering it hard to find an appropriate value for
. This effect however is present also in any other algorithm based on the euclidean distance. - DBSCAN cannot cluster data sets well with large differences in densities, since the minPts-
combination cannot be chosen appropriately for all clusters then.
See the section on extensions below for algorithmic modifications to handle these issues.
Parameter estimation
Every data mining task has the problem of parameters. Every parameter influences the algorithm in specific ways. For DBSCAN the parameters and MinPts are needed. The parameters must be specified by the user of the algorithms since other data sets and other questions require different parameters. An initial value for can be determined by a k-distance graph. As a rule of thumb, 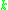can be derived from the number of dimensions in the data set as 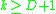. However, larger values are usually better for data sets with noise.Although this parameter estimation gives a sufficient initial parameter set the resulting clustering can turn out to be not the expected partitioning. Therefore research has been performed on incrementally optimizing the parameters against a specific target value.
OPTICS
OPTICS algorithm
OPTICS is an algorithm for finding density-based clusters in spatial data. It was presented by Mihael Ankerst, Markus M. Breunig, Hans-Peter Kriegel and Jörg Sander....
can be seen as a generalization of DBSCAN that replaces the
parameter with a maximum value that mostly effects performance. MinPts then essentially becomes the minimum cluster size to find. While the algorithm is a lot easier to parameterize than DBSCAN, the results are a bit more difficult to use, as it will usually produce a hierarchical clustering instead of the simple data partitioning that DBSCAN produces.Generalization
Generalized DBSCAN or GDBSCAN is a generalization by the same authors to arbitrary "neighborhood" and "dense" predicates. The and minpts parameters are removed from the original algorithm and moved to the predicates. For example on polygon data, the "neighborhood" could be any intersecting polygon, whereas the density predicate uses the polygon areas instead of just the object count.Extensions
The basic DBSCAN algorithm has been used as a base for many other developments, such as parallelisation by Domenica Arlia and Massimo Coppola or an enhancement of the data set background to support uncertain dataUncertain data
In computer science, uncertain data is the notion of data that contains specific uncertainty. Uncertain data is typically found in the area of sensor networks. When representing such data in a database, some indication of the probability of the various values....
presented by Dirk Habich and Peter Benjamin Volk. The basic idea has been extended to hierarchical clustering by the OPTICS algorithm
OPTICS algorithm
OPTICS is an algorithm for finding density-based clusters in spatial data. It was presented by Mihael Ankerst, Markus M. Breunig, Hans-Peter Kriegel and Jörg Sander....
. DBSCAN is also used as part of subspace clustering algorithms like PreDeCon and SUBCLU
SUBCLU
SUBCLU is an algorithm for clustering high-dimensional data by Karin Kailing, Hans-Peter Kriegel and Peer Kröger. It is a subspace clustering algorithm that builds on the density-based clustering algorithm DBSCAN...
.
Availability
An example implementation of DBSCAN is available in the ELKI framework. Notice that this implementation is not optimized for speed but for extensibility. Thus, this implementation can use various index structures for sub-quadratic performance and supports various distance functions and arbitrary data types, but it may be outperformed by low-level optimized implementations on small data sets.External links
- DBSCAN clustering using C++ by Antonio Gulli (No index support, quadratic time and memory complexity, vector data only, some distance functions)
- R package fpc includes DBSCAN (No index support, quadratic complexity, accepts distance matrices)