Darboux derivative
Encyclopedia
The Darboux derivative of a map between a manifold
and a Lie group
is a variant of the standard derivative. In a certain sense, it is arguably a more natural generalization of the single-variable derivative. It allows a generalization of the single-variable fundamental theorem of calculus
to higher dimensions, in a different vein than the generalization that is Stokes' theorem
.
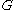be a Lie group
, and let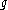
be its Lie algebra
. The Maurer-Cartan form
,
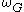, is the smooth 
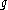-valued 
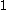-form on 
(cf. Lie algebra valued form) defined by
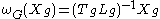
for all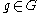
and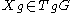 
. Here 
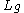denotes left multiplication by the element 
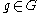and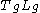 
is its derivative at 
.
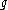Let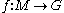
be a smooth function
between a smooth manifold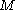
and 
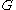. Then the Darboux derivative of 
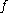is the smooth 
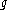-valued 
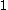-form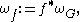
the pullback of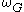
by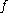 
. The map 
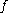is called an integral or primitive of 
.
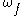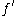of a function 
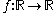assigns to each point in the domain a single number. According to the more general manifold ideas of derivatives, the derivative assigns to each point in the domain a linear map from the tangent space at the domain point to the tangent space at the image point. This derivative encapsulates two pieces of data: the image of the domain point and the linear map. In single-variable calculus, we drop some information. We retain only the linear map, in the form of a scalar multiplying agent (i.e. a number).
One way to justify this convention of retaining only the linear map aspect of the derivative is to appeal to the (very simple) Lie group structure of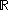
under addition. The tangent bundle
of any Lie group
can be trivialized via left (or right) multiplication. This means that every tangent space in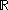
may be identified with the tangent space at the identity, 
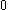, which is the Lie algebra
of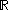
. In this case, left and right multiplication are simply translation. By post-composing the manifold-type derivative with the tangent space trivialization, for each point in the domain we obtain a linear map from the tangent space at the domain point to the Lie algebra of 
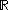. In symbols, for each 
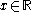we look at the map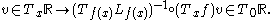
Since the tangent spaces involved are one-dimensional, this linear map is just multiplication by some scalar. (This scalar can change depending on what basis we use for the vector spaces, but the canonical unit vector field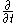
on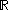 
gives a canonical choice of basis, and hence a canonical choice of scalar.) This scalar is what we usually denote by 
.
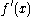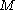is connected, and 
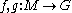are both primitives of 
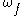, i.e. 
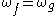, then there exists some constant 
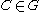such that
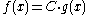for all 
.
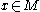This constant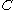
is of course the analogue of the constant that appears when taking an indefinite integral.
:
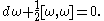
This means that for all vector fields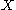
and 
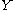on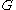 
and all 
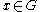, we have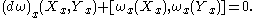
For any Lie algebra-valued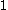
-form on any smooth manifold, all the terms in this equation make sense, so for any such form we can ask whether or not it satisfies this structural equation.
The usual fundamental theorem of calculus
for single-variable calculus has the following local generalization.
If a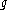
-valued 
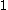-form 
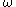on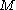 
satisfies the structural equation, then every point 
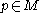has an open neighborhood 
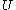and a smooth map 
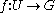such that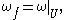
i.e.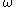
has a primitive defined in a neighborhood of every point of 
.
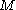For a global generalization of the fundamental theorem, one needs to study certain monodromy
questions in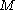
and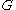 
.
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
and a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
is a variant of the standard derivative. In a certain sense, it is arguably a more natural generalization of the single-variable derivative. It allows a generalization of the single-variable fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
to higher dimensions, in a different vein than the generalization that is Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
.
Formal definition
Let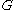 be a Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, and let
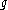be its Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
. The Maurer-Cartan form
Maurer-Cartan form
In mathematics, the Maurer–Cartan form for a Lie group G is a distinguished differential one-form on G that carries the basic infinitesimal information about the structure of G...
,
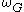, is the smooth 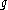-valued 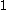-form on 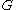(cf. Lie algebra valued form) defined by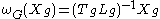for all
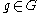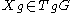and . Here 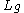denotes left multiplication by the element 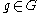and 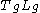is its derivative at 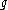.Let
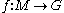be a smooth functionSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
between a smooth manifold
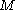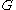and . Then the Darboux derivative of 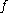is the smooth 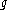-valued 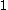-form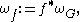the pullback of
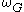by 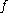. The map 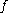is called an integral or primitive of 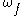.More natural?
The reason that one might call the Darboux derivative a more natural generalization of the derivative of single-variable calculus is this. In single-variable calculus, the derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
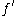of a function 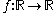assigns to each point in the domain a single number. According to the more general manifold ideas of derivatives, the derivative assigns to each point in the domain a linear map from the tangent space at the domain point to the tangent space at the image point. This derivative encapsulates two pieces of data: the image of the domain point and the linear map. In single-variable calculus, we drop some information. We retain only the linear map, in the form of a scalar multiplying agent (i.e. a number).One way to justify this convention of retaining only the linear map aspect of the derivative is to appeal to the (very simple) Lie group structure of
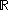under addition. The tangent bundleTangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of any Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
can be trivialized via left (or right) multiplication. This means that every tangent space in
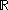may be identified with the tangent space at the identity, 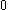, which is the Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of
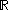. In this case, left and right multiplication are simply translation. By post-composing the manifold-type derivative with the tangent space trivialization, for each point in the domain we obtain a linear map from the tangent space at the domain point to the Lie algebra of 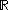. In symbols, for each 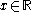we look at the map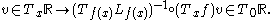Since the tangent spaces involved are one-dimensional, this linear map is just multiplication by some scalar. (This scalar can change depending on what basis we use for the vector spaces, but the canonical unit vector field
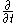on 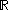gives a canonical choice of basis, and hence a canonical choice of scalar.) This scalar is what we usually denote by 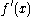.Uniqueness of primitives
If the manifold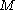 is connected, and 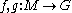are both primitives of 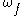, i.e. 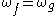, then there exists some constant 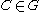such that 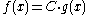for all 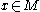.This constant
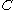is of course the analogue of the constant that appears when taking an indefinite integral.The fundamental theorem of calculus
Recall the structural equation for the Maurer-Cartan formMaurer-Cartan form
In mathematics, the Maurer–Cartan form for a Lie group G is a distinguished differential one-form on G that carries the basic infinitesimal information about the structure of G...
:
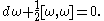
This means that for all vector fields
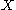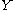and on 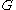and all 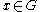, we have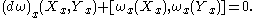For any Lie algebra-valued
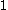-form on any smooth manifold, all the terms in this equation make sense, so for any such form we can ask whether or not it satisfies this structural equation.The usual fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
for single-variable calculus has the following local generalization.
If a
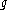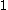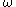-valued -form on 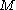satisfies the structural equation, then every point 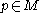has an open neighborhood 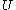and a smooth map 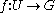such that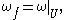i.e.
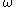has a primitive defined in a neighborhood of every point of 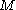.For a global generalization of the fundamental theorem, one needs to study certain monodromy
Monodromy
In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology and algebraic and differential geometry behave as they 'run round' a singularity. As the name implies, the fundamental meaning of monodromy comes from 'running round singly'...
questions in
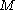and 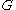.