Darboux frame
Encyclopedia
In the differential geometry of surface
s, a Darboux frame is a natural moving frame
constructed on a surface. It is the analog of the Frenet–Serret frame as applied to surface geometry. A Darboux frame exists at any non-umbilic point of a surface embedded in Euclidean space
. It is named after French mathematician Jean Gaston Darboux
.
The triple T,u,t defines an orthonormal basis
attached to each point of the curve: a natural moving frame along the embedded curve.
Since the tangent vectors are the same in both cases, there is a unique angle α such that a rotation in the plane of N and B produces the pair t and u:
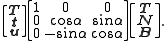
Taking a differential, and applying the Frenet–Serret formulas yields
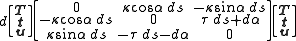
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
s, a Darboux frame is a natural moving frame
Moving frame
In mathematics, a moving frame is a flexible generalization of the notion of an ordered basis of a vector space often used to study the extrinsic differential geometry of smooth manifolds embedded in a homogeneous space.-Introduction:...
constructed on a surface. It is the analog of the Frenet–Serret frame as applied to surface geometry. A Darboux frame exists at any non-umbilic point of a surface embedded in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. It is named after French mathematician Jean Gaston Darboux
Jean Gaston Darboux
Jean-Gaston Darboux was a French mathematician.-Life:Darboux made several important contributions to geometry and mathematical analysis . He was a biographer of Henri Poincaré and he edited the Selected Works of Joseph Fourier.Darboux received his Ph.D...
.
Darboux frame of an embedded curve
Let S be an oriented surface in three-dimensional Euclidean space E3. The construction of Darboux frames on S first considers frames moving along a curve in S, and then specializes when the curves move in the direction of the principal curvatures.Definition
At each point of an oriented surface, one may attach a unit normal u in a unique way. If γ(s) is a curve in S, parametrized by arc length, then the Darboux frame of γ is defined by-
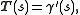(the unit tangent) -
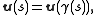(the unit normal) -
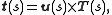(the tangent normal)
The triple T,u,t defines an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
attached to each point of the curve: a natural moving frame along the embedded curve.
Geodesic curvature, normal curvature, and relative torsion
Note that a Darboux frame for a curve does not yield a natural moving frame on the surface, since it still depends on an initial choice of tangent vector. To obtain a moving frame on the surface, we first compare the Darboux frame of γ with its Frenet–Serret frame. Let-
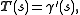(the unit tangent, as above) -
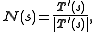(the Frenet normal vector) -
(the Frenet binormal vector).
Since the tangent vectors are the same in both cases, there is a unique angle α such that a rotation in the plane of N and B produces the pair t and u:
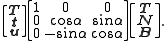
Taking a differential, and applying the Frenet–Serret formulas yields
-
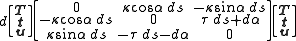
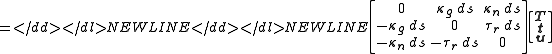
where:- κg is the geodesic curvature of the curve,
- κn is the normal curvature of the curve, and
- τr is the relative torsion (also called geodesic torsion) of the curve.
Darboux frame on a surface
This section specializes the case of the Darboux frame on a curve to the case when the curve is a principal curve of the surface (a line of curvature). In that case, since the principal curves are canonically associated to a surface at all non-umbilic points, the Darboux frame is a canonical moving frameMoving frameIn mathematics, a moving frame is a flexible generalization of the notion of an ordered basis of a vector space often used to study the extrinsic differential geometry of smooth manifolds embedded in a homogeneous space.-Introduction:...
.
The trihedron
The introduction of the trihedron (or trièdre), an invention of Darboux, allows for a conceptual simplification of the problem of moving frames on curves and surfaces by treating the coordinates of the point on the curve and the frame vectors in a uniform manner. A trihedron consists of a point P in Euclidean space, and three orthonormal vectors e1, e2, and e3 based at the point P. A moving trihedron is a trihedron whose components depend on one or more parameters. For example, a trihedron moves along a curve if the point P depends on a single parameter s, and P(s) traces out the curve. Similarly, if P(s,t) depends on a pair of parameters, then this traces out a surface.
A trihedron is said to be adapted to a surface if P always lies on the surface and e3 is the oriented unit normal to the surface at P. In the case of the Darboux frame along an embedded curve, the quadruple
- (P(s) = γ(s), e1(s) = T(s), e2(s) = t(s), e3(s) = u(s))
defines a tetrahedron adapted to the surface into which the curve is embedded.
In terms of this trihedron, the structural equations read
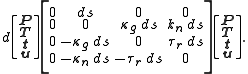
Change of frame
Suppose that any other adapted trihedron
is given for the embedded curve. Since, by definition, P remains the same point on the curve as for the Darboux trihedron, and e3 = u is the unit normal, this new trihedron is related to the Darboux trihedron by a rotation of the form
where θ = θ(s) is a function of s. Taking a differential and applying the Darboux equation yields
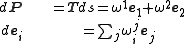
where the (ωi,ωij) are functions of s, satisfying
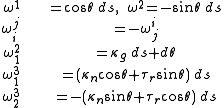
Structure equations
The Poincaré lemma, applied to each double differential ddP, ddei, yields the following Cartan structure equations. From ddP = 0,
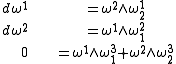
From ddei = 0,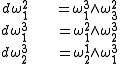
The latter are the Gauss–Codazzi equations for the surface, expressed in the language of differential forms.
Principal curves
Consider the second fundamental form of S. This is the symmetric 2-form on S given by
By the spectral theoremSpectral theoremIn mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
, there is some choice of frame (ei) in which (iiij) is a diagonal matrixDiagonal matrixIn linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
. The eigenvalues are the principal curvatures of the surface. A diagonalizing frame a1, a2, a3 consists of the normal vector a3, and two principal directions a1 and a2. This is called a Darboux frame on the surface. The frame is canonically defined (by an ordering on the eigenvalues, for instance) away from the umbilics of the surface.
Moving frames
The Darboux frame is an example of a natural moving frameMoving frameIn mathematics, a moving frame is a flexible generalization of the notion of an ordered basis of a vector space often used to study the extrinsic differential geometry of smooth manifolds embedded in a homogeneous space.-Introduction:...
defined on a surface. With slight modifications, the notion of a moving frame can be generalized to a hypersurfaceHypersurfaceIn geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
in an n-dimensional Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, or indeed any embedded submanifoldSubmanifoldIn mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
. This generalization is among the many contributions of Élie CartanÉlie CartanÉlie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
to the method of moving frames.
Frames on Euclidean space
A (Euclidean) frame on the Euclidean space En is a higher-dimensional analog of the trihedron. It is defined to be an (n + 1)-tuple of vectors drawn from En, (v; f1, \dots, fn), where:- v is a choice of originOrigin (mathematics)In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
of En, and - (f1, ..., fn) is an orthonormal basisOrthonormal basisIn mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of the vector space based at v.
Let F(n) be the ensemble of all Euclidean frames. The Euclidean groupEuclidean groupIn mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
acts on F(n) as follows. Let φ ∈ Euc(n) be an element of the Euclidean group decomposing as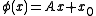
where A is an orthogonal transformation and x0 is a translation. Then, on a frame,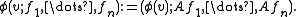
Geometrically, the affine group moves the origin in the usual way, and it acts via a rotation on the orthogonal basis vectors since these are "attached" to the particular choice of origin. This is an effective and transitive group actionGroup actionIn algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
, so F(n) is a principal homogeneous spacePrincipal homogeneous spaceIn mathematics, a principal homogeneous space, or torsor, for a group G is a homogeneous space X for G such that the stabilizer subgroup of any point is trivial...
of Euc(n).
Structure equations
Define the following system of functions F(n) → En: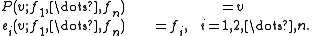
The projection operator P is of special significance. The inverse image of a point P−1(v) consists of all orthonormal bases with basepoint at v. In particular, P : F(n) → En presents F(n) as a principal bundlePrincipal bundleIn mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
whose structure group is the orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(n). (In fact this principal bundle is just the tautological bundle of the homogeneous spaceHomogeneous spaceIn mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
F(n) → F(n)/O(n) = En.)
The exterior derivativeExterior derivativeIn differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
of P (regarded as a vector-valued differential form) decomposes uniquely as
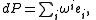
for some system of scalar valued one-formOne-formIn linear algebra, a one-form on a vector space is the same as a linear functional on the space. The usage of one-form in this context usually distinguishes the one-forms from higher-degree multilinear functionals on the space. For details, see linear functional.In differential geometry, a...
s ωi. Similarly, there is an n × n matrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
of one-forms (ωij) such that
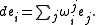
Since the ei are orthonormal under the inner product of Euclidean space, the matrix of 1-forms ωij is skew-symmetric. In particular it is determined uniquely by its upper-triangular part (ωji | i < j). The system of n(n + 1)/2 one-forms (ωi, ωji (i<j)) gives an absolute parallelism of F(n), since the coordinate differentials can each be expressed in terms of them. Under the action of the Euclidean group, these forms transform as follows. Let φ be the Euclidean transformation consisting of a translation vi and rotation matrix (Aji). Then the following are readily checked by the invariance of the exterior derivative under pullback:
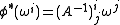
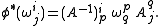
Furthermore, by the Poincaré lemma, one has the following structure equations
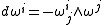
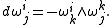
Adapted frames and the Gauss–Codazzi equations
Let φ : M → En be an embedding of a p-dimensional smooth manifold into a Euclidean space. The space of adapted frames on M, denoted here by Fφ(M) is the collection of tuples (x; f1,...,fn) where x ∈ M, and the fi form an orthonormal basis of En such that f1,...,fp are tangent to φ(M) at φ(v).
Several examples of adapted frames have already been considered. The first vector T of the Frenet–Serret frame (T, N, B) is tangent to a curve, and all three vectors are mutually orthonormal. Similarly, the Darboux frame on a surface is an orthonormal frame whose first two vectors are tangent to the surface. Adapted frames are useful because the invariant forms (ωi,ωji) pullback along φ, and the structural equations are preserved under this pullback. Consequently, the resulting system of forms yields structural information about how M is situated inside Euclidean space. In the case of the Frenet–Serret frame, the structural equations are precisely the Frenet–Serret formulas, and these serve to classify curves completely up to Euclidean motions. The general case is analogous: the structural equations for an adapted system of frames classifies arbitrary embedded submanifolds up to a Euclidean motion.
In detail, the projection π : F(M) → M given by π(x; fi) = x gives F(M) the structure of a principal bundlePrincipal bundleIn mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
on M (the structure group for the bundle is O(p) × O(n − p).) This principal bundle embeds into the bundle of Euclidean frames F(n) by φ(v;fi) := (φ(v);fi) ∈ F(n). Hence it is possible to define the pullbacks of the invariant forms from F(n):
Since the exterior derivative is equivariant under pullbacks, the following structural equations hold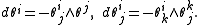
Furthermore, because some of the frame vectors f1...fp are tangent to M while the others are normal, the structure equations naturally split into their tangential and normal contributions. Let the lowercase Latin indices a,b,c range from 1 to p (i.e., the tangential indices) and the Greek indices μ, γ range from p+1 to n (i.e., the normal indices). The first observation is that
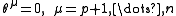
since these forms generate the submanifold φ(M) (in the sense of the Frobenius integration theorem.)
The first set of structural equations now becomes
Of these, the latter implies by Cartan's lemmaCartan's lemmaIn mathematics, Cartan's lemma refers to a number of results named after either Élie Cartan or his son Henri Cartan:* In exterior algebra: Suppose that v1, ..., vp are linearly independent elements of a vector space V and w1, ..., wp are such thatIn mathematics, Cartan's lemma refers to a number of...
that
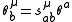
where sμab is symmetric on a and b (the second fundamental forms of φ(M)). Hence, equations (1) are the Gauss formulas (see Gauss–Codazzi equations). In particular, θba is the connection formConnection formIn mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
for the Levi-Civita connectionLevi-Civita connectionIn Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
on M.
The second structural equations also split into the following
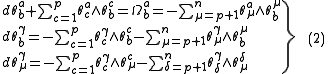
The first equation is the Gauss equation which expresses the curvature formCurvature formIn differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...
Ω of M in terms of the second fundamental form. The second is the Codazzi–Mainardi equation which expresses the covariant derivatives of the second fundamental form in terms of the normal connection. The third is the Ricci equation.