
Datar-Mathews Method for Real Option Valuation
Encyclopedia
The Datar-Mathews Method (DM Method ©
) is a new method for Real options valuation. The DM Method can be understood as an extension of the net present value
(NPV) multi-scenario Monte Carlo model with an adjustment for risk-aversion and economic decision-making. The method uses information that arises naturally in a standard discounted cash flow (DCF), or NPV, project financial valuation. It was created in 2000 by Professor Vinay Datar, Seattle University
, and Scott H. Mathews, Technical Fellow, The Boeing Company.
of operating profits at µ, the market risk rate, and discounting the distribution of the discretionary investment at r, risk-free rate, BEFORE the expected payoff is calculated. The option value is then the expected value of the maximum of the difference between the two discounted distributions or zero. Fig. 1.
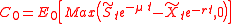
The differential discount rate for μ and r implicitly allows the DM Method to account for the underlying risk. If μ > r, then the option will be risk-averse, typical for both financial and real options. If μ < r, then the option will be risk-seeking. If μ = r, then this is termed a risk-neutral option, and has parallels with NPV-type analyses with decision-making, such as decision tree
s. The DM Method gives the same results as the Black–Scholes and the binomial lattice
option models, provided the same inputs and the discount methods are used. This non-traded real option value therefore is dependent on the risk perception of the evaluator toward the market under assessment relative to privately held investment funds. The DM Method is advantageous for use in real option applications because unlike some other option models it does not require a value for sigma (a measure of uncertainty) or for (the value of the project today), both of which are difficult to derive for new product development projects; see further under Real options valuation. Finally, the DM Method uses real-world values of any distribution type, avoiding the requirement for conversion to risk-neutral values with a lognormal distribution; see further under Monte Carlo methods for option pricing.
Using simulation, for each sample, the engine draws a random variable from both and , calculates their present values, and takes the difference. Fig. 2A. The difference value is compared to zero, the maximum of the two is determined, and the resulting value recorded by the simulation engine. Here, reflecting the optionality inherent in the project, a forecast of a net negative value outcome corresponds to an abandoned project, and has a zero value. Fig. 2B. The resulting values create a payoff distribution representing the economically rational set of plausible, discounted value forecasts of the project at time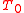 .
.
When sufficient payoff values have been recorded, typically a few hundred, then the mean, or expected value, of the payoff distribution is calculated. Fig. 2C. The option value is the expected value, the first moment of all positive NPVs, of the payoff distribution.
A simple interpretation is:
where Operating Profit and Launch Costs are the appropriately discounted range of cash flows at time 0.
The sampled
distributions
may take any form, although the triangular distribution is often used, as is typical for low data situations. Here, the mean value corresponds to the “Most Likely” scenario, typically the same as for the NPV case. Two other scenarios, “Pessimistic” and “Optimistic”, represent plausible deviations from the Most Likely scenario (often modeled as approximating a 1-out-of-20, or 1-out-of-10 likelihood). This range of probabilistic cases tends to be within the organizational memory bounds of the corporation.
An approximate but conservative option value, termed the DM Range Option, can be estimated simply using range estimates of the present values of operating profit and launch costs. Fig. 3. As described, a range is an estimate of a maximum, most-likely (or mode) and minimum (or Optimistic, Most-Likely, Pessimistic) values that circumscribe a triangular distribution. The two distributions are then combined, and, similar to the approach for simulation described, the expected value is the first moment
of all positive NPVs. Here, using equations from triangular distributions, the mean of the launch cost distribution is calculated. The present value imputed net profit distribution is the difference between the operating profit distribution and the mean value of the launch cost distribution. In one implementation, the approximate option value is the product of the mean and the probability of the payoff distribution right triangle, the positive value right tail. The DM Range Option requires no simulation. This approach is useful for early-stage estimates of project option value when there has not been sufficient time or resources to gather the necessary quantitative information required for a complete cash flow simulation, or in a portfolio of projects when simulation of all the projects is too computationally demanding. If the launch cost is a scalar value, then the range option value calculation is exact. The range option method is similar to the fuzzy method for real options
.
Copyright symbol
The copyright symbol, or copyright sign, designated by © , is the symbol used in copyright notices for works other than sound recordings . The use of the symbol is described in United States copyright law, and, internationally, by the Universal Copyright Convention...
) is a new method for Real options valuation. The DM Method can be understood as an extension of the net present value
Net present value
In finance, the net present value or net present worth of a time series of cash flows, both incoming and outgoing, is defined as the sum of the present values of the individual cash flows of the same entity...
(NPV) multi-scenario Monte Carlo model with an adjustment for risk-aversion and economic decision-making. The method uses information that arises naturally in a standard discounted cash flow (DCF), or NPV, project financial valuation. It was created in 2000 by Professor Vinay Datar, Seattle University
Seattle University
Seattle University is a Jesuit Catholic university located in the First Hill neighborhood of Seattle, Washington, USA.SU is the largest independent university in the Northwest US, with over 7,500 students enrolled in undergraduate and graduate programs within eight schools, and is one of 28 member...
, and Scott H. Mathews, Technical Fellow, The Boeing Company.
The Method
The mathematical equation for the DM Method is shown below. The method captures the real option value by discounting the distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of operating profits at µ, the market risk rate, and discounting the distribution of the discretionary investment at r, risk-free rate, BEFORE the expected payoff is calculated. The option value is then the expected value of the maximum of the difference between the two discounted distributions or zero. Fig. 1.
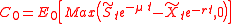
- is a random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
representing the future benefits, or operating profits. The present valuationPresent valuePresent value, also known as present discounted value, is the value on a given date of a future payment or series of future payments, discounted to reflect the time value of money and other factors such as investment risk...
of uses μ, a discount rate consistent with the risk level of . - is a random variable representing the strike priceStrike priceIn options, the strike price is a key variable in a derivatives contract between two parties. Where the contract requires delivery of the underlying instrument, the trade will be at the strike price, regardless of the spot price of the underlying instrument at that time.Formally, the strike...
. The present valuation of uses r, the rate consistent with the risk of investment, . In many generalized option applications, the risk-free discount rate is used. However other discount rates can be considered, such as the corporate bond rate, particularly when the application is a risky corporate product development project. - is the real option value for a single stage project. The option value can be understood as the expected value of the difference of two present value distributions with an economically rational threshold limiting losses on a risk-adjusted basis.
The differential discount rate for μ and r implicitly allows the DM Method to account for the underlying risk. If μ > r, then the option will be risk-averse, typical for both financial and real options. If μ < r, then the option will be risk-seeking. If μ = r, then this is termed a risk-neutral option, and has parallels with NPV-type analyses with decision-making, such as decision tree
Decision tree
A decision tree is a decision support tool that uses a tree-like graph or model of decisions and their possible consequences, including chance event outcomes, resource costs, and utility. It is one way to display an algorithm. Decision trees are commonly used in operations research, specifically...
s. The DM Method gives the same results as the Black–Scholes and the binomial lattice
Binomial options pricing model
In finance, the binomial options pricing model provides a generalizable numerical method for the valuation of options. The binomial model was first proposed by Cox, Ross and Rubinstein in 1979. Essentially, the model uses a “discrete-time” model of the varying price over time of the underlying...
option models, provided the same inputs and the discount methods are used. This non-traded real option value therefore is dependent on the risk perception of the evaluator toward the market under assessment relative to privately held investment funds. The DM Method is advantageous for use in real option applications because unlike some other option models it does not require a value for sigma (a measure of uncertainty) or for (the value of the project today), both of which are difficult to derive for new product development projects; see further under Real options valuation. Finally, the DM Method uses real-world values of any distribution type, avoiding the requirement for conversion to risk-neutral values with a lognormal distribution; see further under Monte Carlo methods for option pricing.
Implementation
The method may be implemented using Monte-Carlo simulation, or in a simplified, approximate form.Using simulation, for each sample, the engine draws a random variable from both and , calculates their present values, and takes the difference. Fig. 2A. The difference value is compared to zero, the maximum of the two is determined, and the resulting value recorded by the simulation engine. Here, reflecting the optionality inherent in the project, a forecast of a net negative value outcome corresponds to an abandoned project, and has a zero value. Fig. 2B. The resulting values create a payoff distribution representing the economically rational set of plausible, discounted value forecasts of the project at time
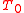 .
.When sufficient payoff values have been recorded, typically a few hundred, then the mean, or expected value, of the payoff distribution is calculated. Fig. 2C. The option value is the expected value, the first moment of all positive NPVs, of the payoff distribution.
A simple interpretation is:

where Operating Profit and Launch Costs are the appropriately discounted range of cash flows at time 0.
The sampled
Sampling (statistics)
In statistics and survey methodology, sampling is concerned with the selection of a subset of individuals from within a population to estimate characteristics of the whole population....
distributions
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
may take any form, although the triangular distribution is often used, as is typical for low data situations. Here, the mean value corresponds to the “Most Likely” scenario, typically the same as for the NPV case. Two other scenarios, “Pessimistic” and “Optimistic”, represent plausible deviations from the Most Likely scenario (often modeled as approximating a 1-out-of-20, or 1-out-of-10 likelihood). This range of probabilistic cases tends to be within the organizational memory bounds of the corporation.
An approximate but conservative option value, termed the DM Range Option, can be estimated simply using range estimates of the present values of operating profit and launch costs. Fig. 3. As described, a range is an estimate of a maximum, most-likely (or mode) and minimum (or Optimistic, Most-Likely, Pessimistic) values that circumscribe a triangular distribution. The two distributions are then combined, and, similar to the approach for simulation described, the expected value is the first moment
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of all positive NPVs. Here, using equations from triangular distributions, the mean of the launch cost distribution is calculated. The present value imputed net profit distribution is the difference between the operating profit distribution and the mean value of the launch cost distribution. In one implementation, the approximate option value is the product of the mean and the probability of the payoff distribution right triangle, the positive value right tail. The DM Range Option requires no simulation. This approach is useful for early-stage estimates of project option value when there has not been sufficient time or resources to gather the necessary quantitative information required for a complete cash flow simulation, or in a portfolio of projects when simulation of all the projects is too computationally demanding. If the launch cost is a scalar value, then the range option value calculation is exact. The range option method is similar to the fuzzy method for real options
Fuzzy Pay-Off Method for Real Option Valuation
Fuzzy Pay-Off Method for Real Option Valuation is a new method for valuing real options, created in 2008. It is based on the use of fuzzy logic and fuzzy numbers for the creation of the pay-off distribution of a possible project...
.

