
Davenport–Schmidt theorem
Encyclopedia
In mathematics
, specifically the area of Diophantine approximation
, the Davenport–Schmidt theorem tells us how well a certain kind of real number
can be approximated by another kind. Specifically it tells us that we can get a good approximation to irrational numbers that are not quadratic by using either quadratic irrational
s or simply rational number
s. It is named after Harold Davenport
and Wolfgang M. Schmidt
.
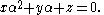
If α is a quadratic irrational we can take x, y, and z to be the coefficients of its minimal polynomial
. If α is rational we will have x = 0. With these integers uniquely determined for each such α we can define the height of α to be
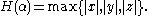
The theorem then says that for any real number ξ which is neither rational nor a quadratic irrational, we can find infinitely many real numbers α which are rational or quadratic irrationals and which satisfy
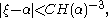
where
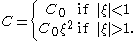
Here we can take C0 to be any real number satisfying C0 > 160/9.
While the theorem is related to Roth's theorem
, its real use lies in the fact that it is effective
, in the sense that the constant C can be worked out for any given ξ.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically the area of Diophantine approximation
Diophantine approximation
In number theory, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real numbers by rational numbers....
, the Davenport–Schmidt theorem tells us how well a certain kind of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
can be approximated by another kind. Specifically it tells us that we can get a good approximation to irrational numbers that are not quadratic by using either quadratic irrational
Quadratic irrational
In mathematics, a quadratic irrational is an irrational number that is the solution to some quadratic equation with rational coefficients...
s or simply rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s. It is named after Harold Davenport
Harold Davenport
Harold Davenport FRS was an English mathematician, known for his extensive work in number theory.-Early life:...
and Wolfgang M. Schmidt
Wolfgang M. Schmidt
Wolfgang M. Schmidt is a mathematician born in 1933. He studied mathematics at the University of Vienna, where he received his PhD, which was supervised by Edmund Hlawka, in 1955...
.
Statement
Given a number α which is either rational or a quadratic irrational, we can find unique integers x, y, and z such that x, y, and z are not all zero, the first non-zero one among them is positive, they are relatively prime, and we have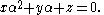
If α is a quadratic irrational we can take x, y, and z to be the coefficients of its minimal polynomial
Minimal polynomial (field theory)
In field theory, given a field extension E / F and an element α of E that is an algebraic element over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p = 0...
. If α is rational we will have x = 0. With these integers uniquely determined for each such α we can define the height of α to be
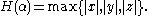
The theorem then says that for any real number ξ which is neither rational nor a quadratic irrational, we can find infinitely many real numbers α which are rational or quadratic irrationals and which satisfy
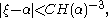
where
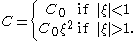
Here we can take C0 to be any real number satisfying C0 > 160/9.
While the theorem is related to Roth's theorem
Thue–Siegel–Roth theorem
In mathematics, the Thue–Siegel–Roth theorem, also known simply as Roth's theorem, is a foundational result in diophantine approximation to algebraic numbers. It is of a qualitative type, stating that a given algebraic number α may not have too many rational number approximations, that are 'very...
, its real use lies in the fact that it is effective
Effective results in number theory
For historical reasons and in order to have application to the solution of Diophantine equations, results in number theory have been scrutinised more than in other branches of mathematics to see if their content is effectively computable...
, in the sense that the constant C can be worked out for any given ξ.

