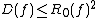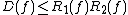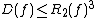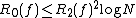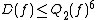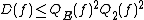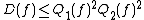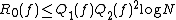Decision tree model
Encyclopedia
In computational complexity
and communication complexity
theories the decision tree model is the model of computation
or communication
in which an algorithm or communication process is considered to be basically a decision tree
, i.e., a sequence of branching operations based on comparisons of some quantities, the comparisons being assigned the unit computational cost.
The branching operations are called "tests" or "queries". In this setting the algorithm in question may be viewed as a computation of a Boolean function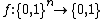
where the input is a series of queries and the output is the final decision. Every query is dependent on previous queries, therefore it is described as a binary tree.
Several variants of decision tree models may be considered, depending on the complexity of the operations allowed in the computation of a single comparison and the way of branching.
Decision trees models are instrumental in establishing lower bounds for computational complexity
for certain classes of computational problems and algorithms: the lower bound for worst-case computational complexity is proportional to the largest depth among the decision trees for all possible inputs for a given computational problem. The computation complexity of a problem or an algorithm expressed in terms of the decision tree model is called decision tree complexity or query complexity.
and searching.
The simplest illustration of this lower bound technique is for the problem of finding the smallest number among n numbers using only comparisons. In this case the decision tree model is a binary tree
. Algorithms for this searching problem may result in n different outcomes (since any of the n given numbers may turn out to be the smallest one). It is known that the depth of a binary tree with n leaves is at least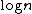
, which gives a lower bound of 
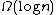for the searching problem. However this lower bound is known to be slack, since the following simple argument shows that at least n - 1 comparisons are needed: Before the smallest number can be determined, every number except the smallest must "lose" (compare greater) in at least one comparison.
Along the same lines the lower bound of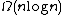
for sorting
may be proved. In this case, the existence of numerous comparison-sorting algorithms having this time complexity, such as mergesort and heapsort
, demonstrates that the bound is tight.
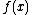, for all 
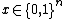, the decision tree is said to "compute" 
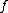. The depth of a tree is the maximum number of queries that can happen before a leaf is reached and a result obtained. 
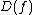, the deterministic decision tree complexity of 
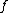is the smallest depth among all deterministic decision trees that compute 
.
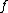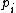. Another equivalent definition is to select a whole decision tree at the beginning from a set of decision trees based on a probability distribution. Based on this second definition, the complexity of the randomized tree is defined as the greatest depth among all the trees associated with probabilities greater than 0. 
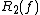is defined as the complexity of the lowest-depth randomized decision tree whose result is 
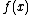with probability at least 
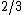for all 
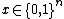(i.e., with bounded 2-sided error).
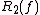is known as the Monte Carlo
randomized decision-tree complexity, because the result is allowed to be incorrect with bounded two-sided error. The Las Vegas
decision-tree complexity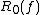
measures the expected depth of a decision tree that must be correct (i.e., has zero-error). There is also a one-sided bounded-error version known as 
.
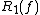of that function. It measures the number of input bits that a nondeterministic algorithm would need to look at in order to evaluate the function with certainty.
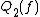is the depth of the lowest-depth quantum decision tree that gives the result 
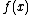with probability at least 
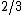for all 
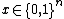. Another quantity, 
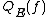, is defined as the depth of the lowest-depth quantum decision tree that gives the result 
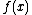with probability 1 in all cases (i.e. computes 
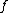exactly). 
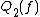and 
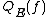are more commonly known as quantum query complexities, because the direct definition of a quantum decision tree is more complicated than in the classical case. Similar to the randomized case, we define 
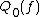and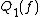 
.
-bit Boolean functions 
,
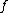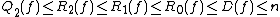, and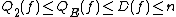 
.
Blum and Impagliazzo, Hartmanis and Hemachandra, and Tardos independently discovered that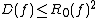
. Nisan found that the Monte Carlo randomized decision tree complexity is also polynomially related to deterministic decision tree complexity: 
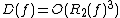. (Nisan also showed that 
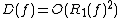.) A corollary of this result is that 
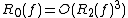. This inequality may be loose, however; no example is known of even a super-linear separation between 
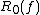and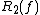 
.
The quantum decision tree complexity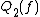
is also polynomially related to 
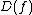. Midrijanis showed that 
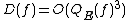, improving a quartic bound due to Beals et al. Beals et al. also showed that 
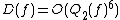, and this is still the best known bound. However, the largest known gap between deterministic and quantum query complexities is only quadratic. A quadratic gap is achieved for the OR function
;
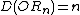while 
.
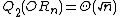It is important to note that these polynomial relationships are valid only for total Boolean functions. For partial Boolean functions, that have a domain a subset of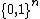
, an exponential separation between 
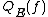and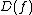 
is possible; the first example of such a problem was discovered by Deutsch and Jozsa
. The same example also gives an exponential separation between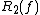
and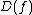 
.
These relationships can be summarized by the following inequalities, which are true up to constant factors:
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
and communication complexity
Communication complexity
The notion of communication complexity was introduced by Yao in 1979,who investigated the following problem involving two separated parties . Alice receives an n-bit string x and Bob another n-bit string y, and the goal is for one of them to compute a certain function f with the least amount of...
theories the decision tree model is the model of computation
Model of computation
In computability theory and computational complexity theory, a model of computation is the definition of the set of allowable operations used in computation and their respective costs...
or communication
Communication
Communication is the activity of conveying meaningful information. Communication requires a sender, a message, and an intended recipient, although the receiver need not be present or aware of the sender's intent to communicate at the time of communication; thus communication can occur across vast...
in which an algorithm or communication process is considered to be basically a decision tree
Decision tree
A decision tree is a decision support tool that uses a tree-like graph or model of decisions and their possible consequences, including chance event outcomes, resource costs, and utility. It is one way to display an algorithm. Decision trees are commonly used in operations research, specifically...
, i.e., a sequence of branching operations based on comparisons of some quantities, the comparisons being assigned the unit computational cost.
The branching operations are called "tests" or "queries". In this setting the algorithm in question may be viewed as a computation of a Boolean function
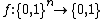where the input is a series of queries and the output is the final decision. Every query is dependent on previous queries, therefore it is described as a binary tree.Several variants of decision tree models may be considered, depending on the complexity of the operations allowed in the computation of a single comparison and the way of branching.
Decision trees models are instrumental in establishing lower bounds for computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
for certain classes of computational problems and algorithms: the lower bound for worst-case computational complexity is proportional to the largest depth among the decision trees for all possible inputs for a given computational problem. The computation complexity of a problem or an algorithm expressed in terms of the decision tree model is called decision tree complexity or query complexity.
Simple decision tree
The model in which every decision is based on the comparison of two numbers within constant time is called simply a decision tree model. It was introduced to establish computational complexity of sortingSorting
Sorting is any process of arranging items in some sequence and/or in different sets, and accordingly, it has two common, yet distinct meanings:# ordering: arranging items of the same kind, class, nature, etc...
and searching.
The simplest illustration of this lower bound technique is for the problem of finding the smallest number among n numbers using only comparisons. In this case the decision tree model is a binary tree
Binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
. Algorithms for this searching problem may result in n different outcomes (since any of the n given numbers may turn out to be the smallest one). It is known that the depth of a binary tree with n leaves is at least
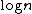, which gives a lower bound of 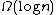for the searching problem. However this lower bound is known to be slack, since the following simple argument shows that at least n - 1 comparisons are needed: Before the smallest number can be determined, every number except the smallest must "lose" (compare greater) in at least one comparison.Along the same lines the lower bound of
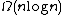for sortingSorting
Sorting is any process of arranging items in some sequence and/or in different sets, and accordingly, it has two common, yet distinct meanings:# ordering: arranging items of the same kind, class, nature, etc...
may be proved. In this case, the existence of numerous comparison-sorting algorithms having this time complexity, such as mergesort and heapsort
Heapsort
Heapsort is a comparison-based sorting algorithm to create a sorted array , and is part of the selection sort family. Although somewhat slower in practice on most machines than a well implemented quicksort, it has the advantage of a more favorable worst-case O runtime...
, demonstrates that the bound is tight.
Deterministic decision tree
If the output of a decision tree is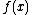, for all 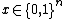, the decision tree is said to "compute" 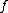. The depth of a tree is the maximum number of queries that can happen before a leaf is reached and a result obtained. 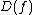, the deterministic decision tree complexity of 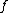is the smallest depth among all deterministic decision trees that compute 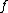.Randomized decision tree
One way to define a randomized decision tree is to add additional nodes to the tree, each controlled by a probability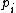. Another equivalent definition is to select a whole decision tree at the beginning from a set of decision trees based on a probability distribution. Based on this second definition, the complexity of the randomized tree is defined as the greatest depth among all the trees associated with probabilities greater than 0. 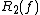is defined as the complexity of the lowest-depth randomized decision tree whose result is 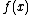with probability at least 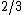for all 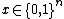(i.e., with bounded 2-sided error). 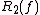is known as the Monte CarloMonte Carlo algorithm
In computing, a Monte Carlo algorithm is a randomized algorithm whose running time is deterministic, but whose output may be incorrect with a certain probability....
randomized decision-tree complexity, because the result is allowed to be incorrect with bounded two-sided error. The Las Vegas
Las Vegas algorithm
In computing, a Las Vegas algorithm is a randomized algorithm that always gives correct results; that is, it always produces the correct result or it informs about the failure. In other words, a Las Vegas algorithm does not gamble with the verity of the result; it gambles only with the resources...
decision-tree complexity
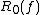measures the expected depth of a decision tree that must be correct (i.e., has zero-error). There is also a one-sided bounded-error version known as 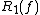.Nondeterministic decision tree
The nondeterministic decision tree complexity of a function is known more commonly as the certificate complexityCertificate (complexity)
In computational complexity theory, a certificate is a string that certifies the answer to a computation, or certifies the membership of some string in a language...
of that function. It measures the number of input bits that a nondeterministic algorithm would need to look at in order to evaluate the function with certainty.
Quantum decision tree
The quantum decision tree complexity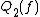 is the depth of the lowest-depth quantum decision tree that gives the result 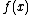with probability at least 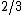for all 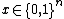. Another quantity, 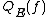, is defined as the depth of the lowest-depth quantum decision tree that gives the result 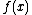with probability 1 in all cases (i.e. computes 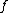exactly). 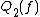and 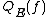are more commonly known as quantum query complexities, because the direct definition of a quantum decision tree is more complicated than in the classical case. Similar to the randomized case, we define 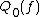and 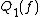.Relationship between different models
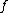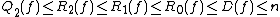It follows immediately from the definitions that for all-bit Boolean functions ,, and 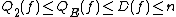.Blum and Impagliazzo, Hartmanis and Hemachandra, and Tardos independently discovered that
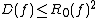. Nisan found that the Monte Carlo randomized decision tree complexity is also polynomially related to deterministic decision tree complexity: 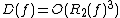. (Nisan also showed that 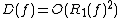.) A corollary of this result is that 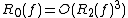. This inequality may be loose, however; no example is known of even a super-linear separation between 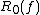and 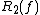.The quantum decision tree complexity
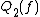is also polynomially related to 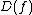. Midrijanis showed that 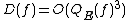, improving a quartic bound due to Beals et al. Beals et al. also showed that 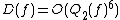, and this is still the best known bound. However, the largest known gap between deterministic and quantum query complexities is only quadratic. A quadratic gap is achieved for the OR functionGrover's algorithm
Grover's algorithm is a quantum algorithm for searching an unsorted database with N entries in O time and using O storage space . It was invented by Lov Grover in 1996....
;
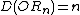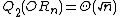while .It is important to note that these polynomial relationships are valid only for total Boolean functions. For partial Boolean functions, that have a domain a subset of
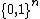, an exponential separation between 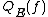and 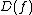is possible; the first example of such a problem was discovered by Deutsch and JozsaDeutsch-Jozsa algorithm
The Deutsch–Jozsa algorithm is a quantum algorithm, proposed by David Deutsch and Richard Jozsa in 1992 with improvements by Richard Cleve, Artur Ekert, Chiara Macchiavello, and Michele Mosca in 1998...
. The same example also gives an exponential separation between
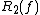and 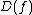.These relationships can be summarized by the following inequalities, which are true up to constant factors:
