Delay differential equation
Encyclopedia
In mathematics
, delay differential equations (DDEs) are a type of differential equation
in which the derivative of the unknown function at a certain time is given in terms of the values of the function at previous times.
A general form of the time-delay differential equation for
is
where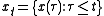
represents the trajectory of the solution in the past. In this equation, 
is a functional operator from
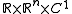to 
with given initial condition
. Then the solution on the interval 
is given by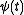 
which is the solution to the inhomogeneous initial value problem
with
. This can be continued for the successive intervals by using the solution to the previous interval as inhomogeneous term. In practice, the initial value problem is often solved numerically.
and 
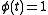. Then the initial value problem can be solved with integration,
i.e.,
, where we picked 
to fit the initial condition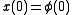 
. Similarly, for the interval
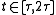we integrate and fit the initial condition to find that 
where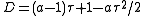 
.
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, delay differential equations (DDEs) are a type of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
in which the derivative of the unknown function at a certain time is given in terms of the values of the function at previous times.
A general form of the time-delay differential equation for
iswhere
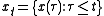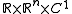represents the trajectory of the solution in the past. In this equation, is a functional operator from to Examples
- Continuous delay
-
- Discrete delay
for 
.
- Linear with discrete delay
- where
.
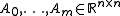- Pantograph equation
- where a, b and λ are constants and 0 < λ < 1. This equation and some more general forms are named after the pantographPantograph (rail)A pantograph for rail lines is a hinged electric-rod device that collects electric current from overhead lines for electric trains or trams. The pantograph typically connects to a one-wire line, with the track acting as the ground wire...
s on trains.
Solving DDEs
DDEs are mostly solved in a stepwise fashion with a principle called the method of steps. For instance, consider the DDE with a single delay
with given initial condition
. Then the solution on the interval is given by 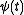which is the solution to the inhomogeneous initial value problemInitial value problem
In mathematics, in the field of differential equations, an initial value problem is an ordinary differential equation together with a specified value, called the initial condition, of the unknown function at a given point in the domain of the solution...
-
,
with
. This can be continued for the successive intervals by using the solution to the previous interval as inhomogeneous term. In practice, the initial value problem is often solved numerically.Example
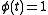Suppose and . Then the initial value problem can be solved with integration,-
,
i.e.,
, where we picked to fit the initial condition 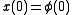. Similarly, for the interval 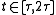we integrate and fit the initial condition to find that where 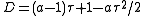.Reduction to ODE
In some cases, delay differential equations are equivalent to a system of ordinary differential equationOrdinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s.
- Example 1 Consider an equation
-
- Introduce
to get a system of ODEs
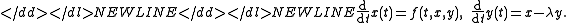
- Example 2 An equation
-
- is equivalent to
- where
The characteristic equation
Similar to ODEOrdinary differential equationIn mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s, many properties of linear DDEs can be characterized and analyzed using the characteristic equation.
The characteristic equation associated with the linear DDE with discrete delays
is-
.
The roots λ of the characteristic equation are called characteristic roots or eigenvalues and the solution set is often referred to as the spectrum. Because of the exponential in the characteristic equation, the DDE has, unlike the ODE case, an infinite number of eigenvalues, making a spectral analysisSpectral theoryIn mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
more involved. The spectrum does however have a some properties which can be exploited in the analysis. For instance, even though there are an infinite number of eigenvalues, there are only a finite number of eigenvalues to the right of any vertical line in the complex plane.
This characteristic equation is a nonlinear eigenproblem and there are many methods to compute the spectrum numerically. In some special situations it is possible to solve the characteristic equation explicitly. Consider, for example, the following DDE: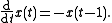
The characteristic equation is
There are an infinite number of solutions to this equation for complex λ. They are given by
,
where
is the kth branch of the Lambert W function.
-
- where
- is equivalent to
- Introduce
