
Dependency relation
Encyclopedia
In mathematics
and computer science
, a dependency relation is a binary relation
that is finite, symmetric
, and reflexive
; i.e. a finite tolerance relation
. That is, it is a finite set of ordered pairs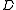 , such that
, such that
In general, dependency relations are not transitive
; thus, they generalize the notion of an equivalence relation
by discarding transitivity.
Let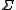 denote the alphabet of all the letters of
denote the alphabet of all the letters of 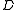 . Then the independency induced by
. Then the independency induced by 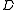 is the binary relation
is the binary relation 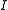
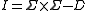
That is, the independency is the set of all ordered pairs that are not in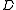 . Clearly, the independency is symmetric and irreflexive.
. Clearly, the independency is symmetric and irreflexive.
The pairs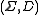 and
and 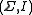 , or the triple
, or the triple  (with
(with 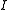 induced by
induced by 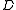 ) are sometimes called the concurrent alphabet or the reliance alphabet.
) are sometimes called the concurrent alphabet or the reliance alphabet.
The pairs of letters in an independency relation induce an equivalence relation on the free monoid of all possible strings of finite length. The elements of the equivalence classes induced by the independency are called traces
, and are studied in trace theory
.
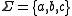 . A possible dependency relation is
. A possible dependency relation is
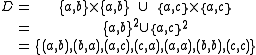
The corresponding independency is
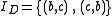
Therefore, the letters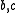 commute, or are independent of one-another.
commute, or are independent of one-another.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a dependency relation is a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
that is finite, symmetric
Symmetric relation
In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
, and reflexive
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
; i.e. a finite tolerance relation
Tolerance relation
In mathematics, a tolerance relation is a relation that is reflexive and symmetric. It does not need to betransitive.-External links:*Gerasin, S. N., Shlyakhov, V. V., and Yakovlev, S. V. 2008. Set coverings and tolerance relations. Cybernetics and Sys. Anal. 44, 3 , 333–340. DOI=...
. That is, it is a finite set of ordered pairs
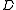 , such that
, such that- If
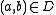 then
then  (symmetric)
(symmetric) - If
 is an element of the set on which the relation is defined, then
is an element of the set on which the relation is defined, then 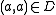 (reflexive)
(reflexive)
In general, dependency relations are not transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
; thus, they generalize the notion of an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
by discarding transitivity.
Let
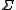 denote the alphabet of all the letters of
denote the alphabet of all the letters of 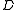 . Then the independency induced by
. Then the independency induced by 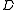 is the binary relation
is the binary relation 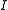
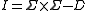
That is, the independency is the set of all ordered pairs that are not in
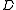 . Clearly, the independency is symmetric and irreflexive.
. Clearly, the independency is symmetric and irreflexive.The pairs
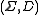 and
and 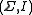 , or the triple
, or the triple  (with
(with 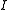 induced by
induced by 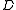 ) are sometimes called the concurrent alphabet or the reliance alphabet.
) are sometimes called the concurrent alphabet or the reliance alphabet.The pairs of letters in an independency relation induce an equivalence relation on the free monoid of all possible strings of finite length. The elements of the equivalence classes induced by the independency are called traces
Trace monoid
In mathematics and computer science, a trace is a set of strings, wherein certain letters in the string are allowed to commute, but others are not. It generalizes the concept of a string, by not forcing the letters to always be in a fixed order, but allowing certain reshufflings to take place...
, and are studied in trace theory
Trace theory
In mathematics and computer science, trace theory aims to provide a concrete mathematical underpinning for the study of concurrent computation and process calculi...
.
Examples
Consider the alphabet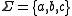 . A possible dependency relation is
. A possible dependency relation is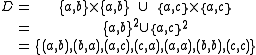
The corresponding independency is
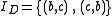
Therefore, the letters
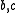 commute, or are independent of one-another.
commute, or are independent of one-another.

