Trace monoid
Encyclopedia
In mathematics
and computer science
, a trace is a set of strings
, wherein certain letters in the string are allowed to commute
, but others are not. It generalizes the concept of a string, by not forcing the letters to always be in a fixed order, but allowing certain reshufflings to take place. Traces are used in theories of concurrent computation, where commuting letters stand for portions of a job
that can execute independently of one-another, while non-commuting letters stand for locks
, synchronization points or thread joins.
The trace monoid or free partially commutative monoid is a monoid
of traces. In a nutshell, it is constructed as follows: sets of commuting letters are given by an independency relation. These induce an equivalence relation
of equivalent strings; the elements of the equivalence classes are the traces. The equivalence relation then partitions up the free monoid (the set of all strings of finite length) into a set of equivalence classes; the result is still a monoid; it is a quotient monoid and is called the trace monoid. The trace monoid is universal
, in that all homomorphic monoids are in fact isomorphic.
Trace monoids are commonly used to model concurrent computation, forming the foundation for process calculi. They are the object of study in trace theory
. The utility of trace monoids comes from the fact that they are isomorphic to the monoid of dependency graph
s; thus allowing algebraic techniques to be applied to graphs, and vice-versa. They are also isomorphic to history monoid
s, which model the history of computation of individual processes in the context of all scheduled processes on one or more computers.
denote the free monoid, that is, the set of all strings written in the alphabet 
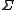. Here, the asterisk denotes, as usual, the Kleene star
. An independency relation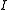
then induces a binary relation
on 
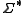, where 
if and only if there exist 
, and a pair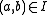 
such that 
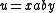and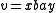 
. Here, 
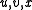and 
are understood to be strings (elements of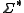 
), while 
and 
are letters (elements of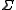 
).
The trace is defined as the symmetric, reflexive and transitive closure
of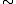
. The trace is thus an equivalence relation
on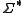
, and is denoted by 
. The subscript D on the equivalence simply denotes that the equivalence is obtained from the independency I induced by the dependency D. Clearly, different dependencies will give different equivalence relations.
The transitive closure simply implies that
if and only if there exists a sequence of strings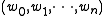 
such that 
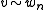and 
and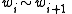 
for all 
.
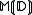, is defined as the quotient monoid
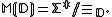
The homomorphism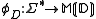
is commonly referred to as the natural homomorphism or canonical homomorphism. That the terms natural or canonical are deserved follows from the fact that this morphism embodies a universal property
, as discussed in a later section.
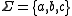. A possible dependency relation is
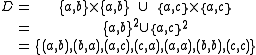
The corresponding independency is
Therefore, the letters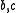
commute. Thus, for example, a trace equivalence class for the string 
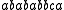would be
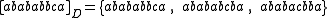
The equivalence class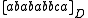
is an element of the trace monoid.
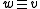, then 
. Here, the notation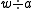 
denotes right cancellation, the removal of the first occurrence of the letter a from the string w, starting from the right-hand side. Equivalence is also maintained by left-cancellation. Several corollaries follow:
A strong form of Levi's lemma holds for traces. Specifically, if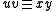
for strings u, v, x, y, then there exist strings 
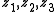and 
such that 
for all letters
and 
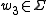such that 
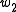occurs in 
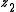and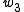 
occurs in 
, and
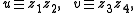
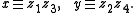
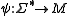
to some monoid M, such that the "usual" trace properties hold, namely:
Dependency morphisms are universal
, in the sense that for a given, fixed dependency D, if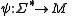
is a dependency morphism to a monoid M, then M is isomorphic to the trace monoid 
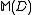. In particular, the natural homomorphism is a dependency morphism.
s for words in trace monoids. One is the lexicographic normal form, due to Anatolij V. Anisimov and Donald Knuth
, and the other is the Foata normal form due to Pierre Cartier
and Dominique Foata
who studied the trace monoid for its combinatorics
in the 1960s.
can be regarded as a subset of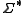
the set of all possible strings, so then a trace language is defined as subset of 
all possible traces.
A language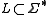
is a trace language, or is said to be consistent with dependency D if
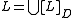
where
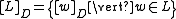
is the trace closure of a set of strings, and
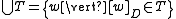
is the set of strings in a set of traces.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a trace is a set of strings
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
, wherein certain letters in the string are allowed to commute
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
, but others are not. It generalizes the concept of a string, by not forcing the letters to always be in a fixed order, but allowing certain reshufflings to take place. Traces are used in theories of concurrent computation, where commuting letters stand for portions of a job
Process (computing)
In computing, a process is an instance of a computer program that is being executed. It contains the program code and its current activity. Depending on the operating system , a process may be made up of multiple threads of execution that execute instructions concurrently.A computer program is a...
that can execute independently of one-another, while non-commuting letters stand for locks
Lock (computer science)
In computer science, a lock is a synchronization mechanism for enforcing limits on access to a resource in an environment where there are many threads of execution. Locks are one way of enforcing concurrency control policies.-Types:...
, synchronization points or thread joins.
The trace monoid or free partially commutative monoid is a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
of traces. In a nutshell, it is constructed as follows: sets of commuting letters are given by an independency relation. These induce an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
of equivalent strings; the elements of the equivalence classes are the traces. The equivalence relation then partitions up the free monoid (the set of all strings of finite length) into a set of equivalence classes; the result is still a monoid; it is a quotient monoid and is called the trace monoid. The trace monoid is universal
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
, in that all homomorphic monoids are in fact isomorphic.
Trace monoids are commonly used to model concurrent computation, forming the foundation for process calculi. They are the object of study in trace theory
Trace theory
In mathematics and computer science, trace theory aims to provide a concrete mathematical underpinning for the study of concurrent computation and process calculi...
. The utility of trace monoids comes from the fact that they are isomorphic to the monoid of dependency graph
Dependency graph
In mathematics, computer science and digital electronics, a dependency graph is a directed graph representing dependencies of several objects towards each other...
s; thus allowing algebraic techniques to be applied to graphs, and vice-versa. They are also isomorphic to history monoid
History monoid
In mathematics and computer science, a history monoid is a way of representing the histories of concurrently running computer processes as a collection of strings, each string representing the individual history of a process...
s, which model the history of computation of individual processes in the context of all scheduled processes on one or more computers.
Trace
Let denote the free monoid, that is, the set of all strings written in the alphabet 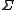. Here, the asterisk denotes, as usual, the Kleene starKleene star
In mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
. An independency relation
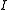then induces a binary relationBinary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
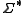on , where if and only if there exist , and a pair 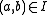such that 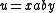and 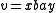. Here, 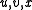and are understood to be strings (elements of 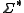), while and are letters (elements of 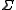).The trace is defined as the symmetric, reflexive and transitive closure
Transitive closure
In mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
of
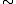. The trace is thus an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on
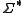, and is denoted by . The subscript D on the equivalence simply denotes that the equivalence is obtained from the independency I induced by the dependency D. Clearly, different dependencies will give different equivalence relations.The transitive closure simply implies that
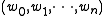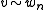if and only if there exists a sequence of strings such that and and 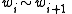for all .Trace monoid
The trace monoid, commonly denoted as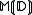, is defined as the quotient monoid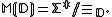The homomorphism
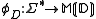
is commonly referred to as the natural homomorphism or canonical homomorphism. That the terms natural or canonical are deserved follows from the fact that this morphism embodies a universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
, as discussed in a later section.
Examples
Consider the alphabet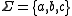. A possible dependency relation is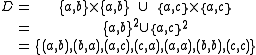The corresponding independency is
Therefore, the letters
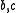commute. Thus, for example, a trace equivalence class for the string 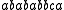would be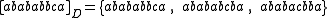The equivalence class
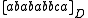is an element of the trace monoid.Properties
The cancellation property states that equivalence is maintained under right cancellation. That is, if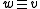, then . Here, the notation 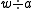denotes right cancellation, the removal of the first occurrence of the letter a from the string w, starting from the right-hand side. Equivalence is also maintained by left-cancellation. Several corollaries follow:- Embedding:
if and only if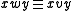 
for strings x and y. Thus, the trace monoid is a syntactic monoidSyntactic monoidIn mathematics and computer science, the syntactic monoid M of a formal language L is the smallest monoid that recognizes the language L.-Syntactic quotient:...
.
- Independence: if
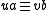and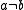 
, then a is independent of b. That is, 
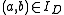. Furthermore, there exists a string w such that 
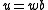and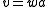 
.
- Projection rule: equivalence is maintained under string projection, so that if
, then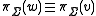 
.
A strong form of Levi's lemma holds for traces. Specifically, if
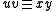for strings u, v, x, y, then there exist strings 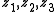and such that for all letters
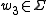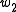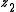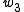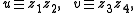
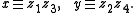
and such that occurs in and occurs in , andUniversal property
A dependency morphism (with respect to a dependency D) is a morphism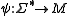to some monoid M, such that the "usual" trace properties hold, namely:
- 1.
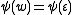implies that 
- 2.
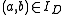implies that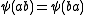 
- 3.
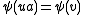implies that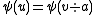 
- 4.
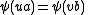and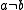 
imply that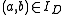 
Dependency morphisms are universal
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
, in the sense that for a given, fixed dependency D, if
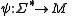is a dependency morphism to a monoid M, then M is isomorphic to the trace monoid 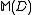. In particular, the natural homomorphism is a dependency morphism.Normal forms
There are two well-known normal formNormal form
Normal form may refer to:* Normal form * Normal form * Normal form * Normal form In formal language theory:* Beta normal form* Chomsky normal form* Greibach normal form* Kuroda normal form...
s for words in trace monoids. One is the lexicographic normal form, due to Anatolij V. Anisimov and Donald Knuth
Donald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
, and the other is the Foata normal form due to Pierre Cartier
Pierre Cartier (mathematician)
Pierre Cartier is a mathematician. An associate of the Bourbaki group and at one time a colleague of Alexander Grothendieck, his interests have ranged over algebraic geometry, representation theory, mathematical physics, and category theory....
and Dominique Foata
Dominique Foata
Dominique Foata is a mathematician who works in enumerative combinatorics. With Pierre Cartier and Marcel-Paul Schützenberger he pioneered the modern approach to classical combinatorics, that lead, in part, to the current blossoming of algebraic combinatorics...
who studied the trace monoid for its combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
in the 1960s.
Trace languages
Just as a formal languageFormal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
can be regarded as a subset of
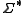the set of all possible strings, so then a trace language is defined as subset of all possible traces.A language
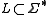is a trace language, or is said to be consistent with dependency D if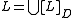where
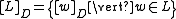
is the trace closure of a set of strings, and
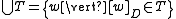
is the set of strings in a set of traces.