
History monoid
Encyclopedia
In mathematics
and computer science
, a history monoid is a way of representing the histories of concurrently running computer processes as a collection of strings
, each string representing the individual history of a process. The history monoid provides a set of synchronization primitives (such as locks
, mutexes or thread joins) for providing rendezvous points between a set of independently executing processes or threads.
History monoids occur in the theory of concurrent computation, and provide a low-level mathematical foundation for process calculi, such as CSP the language of communicating sequential processes
, or CCS, the calculus of communicating systems
. History monoids were first presented by M.W. Shields.
History monoids are isomorphic to trace monoid
s (free partially commutative monoids) and to the monoid
of dependency graph
s. As such, they are free object
s and are universal
. The history monoid is a type of semi-abelian categorical product in the category
of monoids.
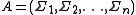
denote an n-tuple of alphabets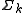 . Let
. Let 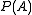 denote all possible combinations of finite-length strings from the alphabets:
denote all possible combinations of finite-length strings from the alphabets:
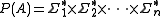
(In more formal language,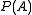 is the Cartesian product
is the Cartesian product
of the free monoids of the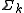 . The superscript star is the Kleene star
. The superscript star is the Kleene star
.) Composition in the product monoid is component-wise, so that, for
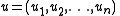
and
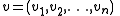
then
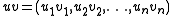
for all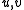 in
in 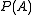 . Define the union alphabet to be
. Define the union alphabet to be
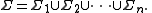
(The union here is the set union, not the disjoint union
.) Given any string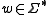 , we can pick out just the letters in some
, we can pick out just the letters in some 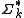 using the corresponding string projection
using the corresponding string projection 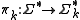 . A distribution
. A distribution 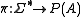 is the mapping that operates on
is the mapping that operates on 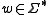 with all of the
with all of the 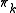 , separating it into components in each free monoid:
, separating it into components in each free monoid:
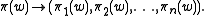
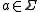 , the tuple
, the tuple 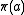 is called the elementary history of a. It serves as an indicator function for the inclusion of a letter a in an alphabet
is called the elementary history of a. It serves as an indicator function for the inclusion of a letter a in an alphabet 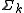 . That is,
. That is,
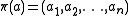
where
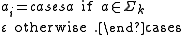
Here, denotes the empty string
denotes the empty string
. The history monoid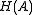 is the free monoid generated by elementary histories. It is clearly a submonoid of the product monoid
is the free monoid generated by elementary histories. It is clearly a submonoid of the product monoid 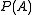 . The elements of
. The elements of 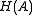 are called global histories, and the projections of a global history are called individual histories.
are called global histories, and the projections of a global history are called individual histories.
of a process (or thread
or machine
); the alphabet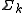 is the set of states of the process.
is the set of states of the process.
A letter that occurs in two or more alphabets serves as a synchronization primitive between the various individual histories. That is, if such a letter occurs in one individual history, it must also occur in another history, and serves to "tie" or "rendezvous" them together.
Consider, for example,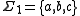 and
and 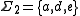 . The union alphabet is of course
. The union alphabet is of course 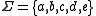 . The elementary histories are
. The elementary histories are 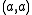 ,
, 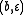 ,
, 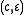 ,
, 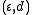 and
and 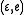 . In this example, an individual history of the first process might be
. In this example, an individual history of the first process might be 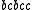 while the individual history of the second machine might be
while the individual history of the second machine might be 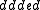 . Both of these individual histories are represented by the global history
. Both of these individual histories are represented by the global history 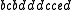 , since the projection of this string onto the individual alphabets yields the individual histories. In the global history, the letter
, since the projection of this string onto the individual alphabets yields the individual histories. In the global history, the letter 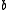 can be considered to commute with the letters
can be considered to commute with the letters 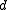 and
and  , in that these can be rearranged without changing the individual histories. Such commutation is simply a statement that the first and second processes are running concurrently, and are unordered with respect to each other; they have not (yet) exchanged any messages or performed any synchronization.
, in that these can be rearranged without changing the individual histories. Such commutation is simply a statement that the first and second processes are running concurrently, and are unordered with respect to each other; they have not (yet) exchanged any messages or performed any synchronization.
The letter serves as a synchronization primitive, as its occurrence marks a spot in both the global and individual histories, that cannot be commuted across. Thus, while the letters
serves as a synchronization primitive, as its occurrence marks a spot in both the global and individual histories, that cannot be commuted across. Thus, while the letters 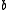 and
and  can be re-ordered past
can be re-ordered past 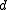 and
and  , they cannot be reordered past
, they cannot be reordered past  . Thus, the global history
. Thus, the global history 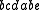 and the global history
and the global history 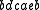 both have as individual histories
both have as individual histories 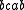 and
and 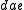 , indicating that the execution of
, indicating that the execution of 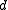 may happen before or after
may happen before or after  . However, the letter
. However, the letter  is synchronizing, so that
is synchronizing, so that  is guaranteed to happen after
is guaranteed to happen after  , even though
, even though  is in a different process than
is in a different process than  .
.
, and as such, is a type of semi-abelian categorical product in the category
of monoids. In particular, the history monoid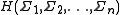 is isomorphic to the trace monoid
is isomorphic to the trace monoid 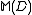 with the dependency relation
with the dependency relation
given by
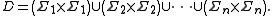
In simple terms, this is just the formal statement of the informal discussion given above: the letters in an alphabet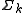 can be commutatively re-ordered past the letters in an alphabet
can be commutatively re-ordered past the letters in an alphabet 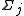 , unless they are letters that occur in both alphabets. Thus, traces are exactly global histories, and vice-versa.
, unless they are letters that occur in both alphabets. Thus, traces are exactly global histories, and vice-versa.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a history monoid is a way of representing the histories of concurrently running computer processes as a collection of strings
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
, each string representing the individual history of a process. The history monoid provides a set of synchronization primitives (such as locks
Lock (computer science)
In computer science, a lock is a synchronization mechanism for enforcing limits on access to a resource in an environment where there are many threads of execution. Locks are one way of enforcing concurrency control policies.-Types:...
, mutexes or thread joins) for providing rendezvous points between a set of independently executing processes or threads.
History monoids occur in the theory of concurrent computation, and provide a low-level mathematical foundation for process calculi, such as CSP the language of communicating sequential processes
Communicating sequential processes
In computer science, Communicating Sequential Processes is a formal language for describing patterns of interaction in concurrent systems. It is a member of the family of mathematical theories of concurrency known as process algebras, or process calculi...
, or CCS, the calculus of communicating systems
Calculus of Communicating Systems
The Calculus of Communicating Systems is a process calculus introduced by Robin Milner around 1980 and the title of a book describing the calculus. Its actions model indivisible communications between exactly two participants. The formal language includes primitives for describing parallel...
. History monoids were first presented by M.W. Shields.
History monoids are isomorphic to trace monoid
Trace monoid
In mathematics and computer science, a trace is a set of strings, wherein certain letters in the string are allowed to commute, but others are not. It generalizes the concept of a string, by not forcing the letters to always be in a fixed order, but allowing certain reshufflings to take place...
s (free partially commutative monoids) and to the monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
of dependency graph
Dependency graph
In mathematics, computer science and digital electronics, a dependency graph is a directed graph representing dependencies of several objects towards each other...
s. As such, they are free object
Free object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
s and are universal
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
. The history monoid is a type of semi-abelian categorical product in the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of monoids.
Product monoids and projection
Let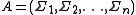
denote an n-tuple of alphabets
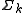 . Let
. Let 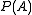 denote all possible combinations of finite-length strings from the alphabets:
denote all possible combinations of finite-length strings from the alphabets: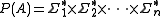
(In more formal language,
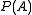 is the Cartesian product
is the Cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of the free monoids of the
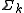 . The superscript star is the Kleene star
. The superscript star is the Kleene starKleene star
In mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
.) Composition in the product monoid is component-wise, so that, for
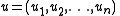
and
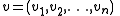
then
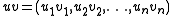
for all
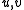 in
in 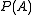 . Define the union alphabet to be
. Define the union alphabet to be
(The union here is the set union, not the disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
.) Given any string
 , we can pick out just the letters in some
, we can pick out just the letters in some  using the corresponding string projection
using the corresponding string projection  . A distribution
. A distribution 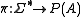 is the mapping that operates on
is the mapping that operates on 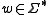 with all of the
with all of the 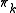 , separating it into components in each free monoid:
, separating it into components in each free monoid: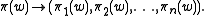
Histories
For every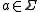 , the tuple
, the tuple 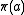 is called the elementary history of a. It serves as an indicator function for the inclusion of a letter a in an alphabet
is called the elementary history of a. It serves as an indicator function for the inclusion of a letter a in an alphabet 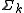 . That is,
. That is,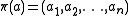
where
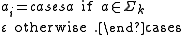
Here,
 denotes the empty string
denotes the empty stringEmpty string
In computer science and formal language theory, the empty string is the unique string of length zero. It is denoted with λ or sometimes Λ or ε....
. The history monoid
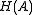 is the free monoid generated by elementary histories. It is clearly a submonoid of the product monoid
is the free monoid generated by elementary histories. It is clearly a submonoid of the product monoid 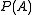 . The elements of
. The elements of 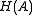 are called global histories, and the projections of a global history are called individual histories.
are called global histories, and the projections of a global history are called individual histories.Connection to computer science
The use of the word history in this context, and the connection to concurrent computing, can be understood as follows. An individual history is a record of the sequence of statesState (computer science)
In computer science and automata theory, a state is a unique configuration of information in a program or machine. It is a concept that occasionally extends into some forms of systems programming such as lexers and parsers....
of a process (or thread
Thread (computer science)
In computer science, a thread of execution is the smallest unit of processing that can be scheduled by an operating system. The implementation of threads and processes differs from one operating system to another, but in most cases, a thread is contained inside a process...
or machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
); the alphabet
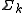 is the set of states of the process.
is the set of states of the process.A letter that occurs in two or more alphabets serves as a synchronization primitive between the various individual histories. That is, if such a letter occurs in one individual history, it must also occur in another history, and serves to "tie" or "rendezvous" them together.
Consider, for example,
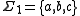 and
and 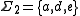 . The union alphabet is of course
. The union alphabet is of course 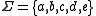 . The elementary histories are
. The elementary histories are 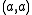 ,
, 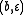 ,
, 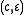 ,
, 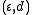 and
and 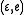 . In this example, an individual history of the first process might be
. In this example, an individual history of the first process might be 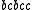 while the individual history of the second machine might be
while the individual history of the second machine might be 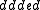 . Both of these individual histories are represented by the global history
. Both of these individual histories are represented by the global history 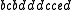 , since the projection of this string onto the individual alphabets yields the individual histories. In the global history, the letter
, since the projection of this string onto the individual alphabets yields the individual histories. In the global history, the letter 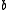 can be considered to commute with the letters
can be considered to commute with the letters 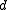 and
and  , in that these can be rearranged without changing the individual histories. Such commutation is simply a statement that the first and second processes are running concurrently, and are unordered with respect to each other; they have not (yet) exchanged any messages or performed any synchronization.
, in that these can be rearranged without changing the individual histories. Such commutation is simply a statement that the first and second processes are running concurrently, and are unordered with respect to each other; they have not (yet) exchanged any messages or performed any synchronization.The letter
 serves as a synchronization primitive, as its occurrence marks a spot in both the global and individual histories, that cannot be commuted across. Thus, while the letters
serves as a synchronization primitive, as its occurrence marks a spot in both the global and individual histories, that cannot be commuted across. Thus, while the letters 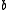 and
and  can be re-ordered past
can be re-ordered past 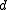 and
and  , they cannot be reordered past
, they cannot be reordered past  . Thus, the global history
. Thus, the global history 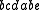 and the global history
and the global history 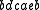 both have as individual histories
both have as individual histories 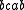 and
and 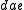 , indicating that the execution of
, indicating that the execution of 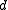 may happen before or after
may happen before or after  . However, the letter
. However, the letter  is synchronizing, so that
is synchronizing, so that  is guaranteed to happen after
is guaranteed to happen after  , even though
, even though  is in a different process than
is in a different process than  .
.Properties
The history monoid is isomorphic to the trace monoidTrace monoid
In mathematics and computer science, a trace is a set of strings, wherein certain letters in the string are allowed to commute, but others are not. It generalizes the concept of a string, by not forcing the letters to always be in a fixed order, but allowing certain reshufflings to take place...
, and as such, is a type of semi-abelian categorical product in the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of monoids. In particular, the history monoid
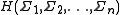 is isomorphic to the trace monoid
is isomorphic to the trace monoid 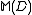 with the dependency relation
with the dependency relationDependency relation
In mathematics and computer science, a dependency relation is a binary relation that is finite, symmetric, and reflexive; i.e. a finite tolerance relation...
given by
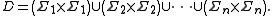
In simple terms, this is just the formal statement of the informal discussion given above: the letters in an alphabet
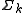 can be commutatively re-ordered past the letters in an alphabet
can be commutatively re-ordered past the letters in an alphabet 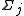 , unless they are letters that occur in both alphabets. Thus, traces are exactly global histories, and vice-versa.
, unless they are letters that occur in both alphabets. Thus, traces are exactly global histories, and vice-versa.

