Descriptive complexity
Encyclopedia
Descriptive complexity is a branch of computational complexity theory
and of finite model theory
that characterizes complexity class
es by the type of logic
needed to express the languages in them. For example, PH, the union of all complexity classes in the polynomial hierarchy, is precisely the class of languages expressible by statements of second-order logic
. This connection between complexity and the logic of finite structures allows results to be transferred easily from one area to the other, facilitating new proof methods and providing additional evidence that the main complexity classes are somehow "natural" and not tied to the specific abstract machine
s used to define them.
Specifically, each logical system produces a set of queries
expressible in it. The queries – when restricted to finite structures – correspond to the computational problem
s of traditional complexity theory.
The first main result of descriptive complexity was Fagin's theorem
, shown by Ronald Fagin
in 1974. It established that NP
is precisely the set of languages expressible by sentences of existential second-order logic
; that is, second order logic excluding universal quantification over relations, functions, and subsets. Many other classes were later characterized in such a manner, most of them by Neil Immerman
:
More precise definitions of those classes can be found on the articles SO
and FO
.
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
and of finite model theory
Finite model theory
Finite Model Theory is a subarea of model theory . MT is the branch of mathematical logic which deals with the relation between a formal language and its interpretations . FMT is a restriction of MT to interpretations of finite structures, i.e...
that characterizes complexity class
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
es by the type of logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
needed to express the languages in them. For example, PH, the union of all complexity classes in the polynomial hierarchy, is precisely the class of languages expressible by statements of second-order logic
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
. This connection between complexity and the logic of finite structures allows results to be transferred easily from one area to the other, facilitating new proof methods and providing additional evidence that the main complexity classes are somehow "natural" and not tied to the specific abstract machine
Abstract machine
An abstract machine, also called an abstract computer, is a theoretical model of a computer hardware or software system used in automata theory...
s used to define them.
Specifically, each logical system produces a set of queries
Query (complexity)
In descriptive complexity, a query is a mapping from structures of one signature to structures of another vocabulary. Neil Immerman, in his book "Descriptive Complexity", "use[s] the concept of query as the fundamental paradigm of computation" ....
expressible in it. The queries – when restricted to finite structures – correspond to the computational problem
Computational problem
In theoretical computer science, a computational problem is a mathematical object representing a collection of questions that computers might want to solve. For example, the problem of factoring...
s of traditional complexity theory.
The first main result of descriptive complexity was Fagin's theorem
Fagin's theorem
Fagin's theorem is a result in descriptive complexity theory that states that the set of all properties expressible in existential second-order logic is precisely the complexity class NP...
, shown by Ronald Fagin
Ronald Fagin
Ronald Fagin is the Manager of the Foundations of Computer Science group at the IBM Almaden Research Center. He is best known for his pioneering work in database theory, finite model theory, and reasoning about knowledge...
in 1974. It established that NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
is precisely the set of languages expressible by sentences of existential second-order logic
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
; that is, second order logic excluding universal quantification over relations, functions, and subsets. Many other classes were later characterized in such a manner, most of them by Neil Immerman
Neil Immerman
Neil Immerman is an American theoretical computer scientist, a professor of computer science at the University of Massachusetts Amherst...
:
- First-order logicFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
defines the class FOFO (complexity)FO is the complexity class of structures which can be recognised by formulae of first-order logic. It is the foundation of the field of descriptive complexity and is equal to the complexity class AC0 FO-regular...
, corresponding to AC0AC0AC0 is a complexity class used in circuit complexity. It is the smallest class in the AC hierarchy, and consists of all families of circuits of depth O and polynomial size, with unlimited-fanin AND gates and OR gates....
, the languages recognized by polynomial-size circuits of bounded depth, which equals the languages recognized by a concurrent random access machine in constant time. - First-order logic with a commutative, transitive closureTransitive closureIn mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
operator added yields SLSL (complexity)In computational complexity theory, SL is the complexity class of problems log-space reducible to USTCON , which is the problem of determining whether there exists a path between two vertices in an undirected graph, otherwise described as the problem of determining whether two vertices are in the...
, which equals LL (complexity)In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space...
, problems solvable in logarithmic space. - First-order logic with a transitive closureTransitive closureIn mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
operator yields NLNL (complexity)In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space....
, the problems solvable in nondeterministic logarithmic space. - In the presence of linear order, first-order logic with a least fixed pointLeast fixed pointIn order theory, a branch of mathematics, the least fixed point of a function is the fixed point which is less than or equal to all other fixed points, according to some partial order....
operator gives PP (complexity)In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
, the problems solvable in deterministic polynomial time. - Existential second-order logic yields NPNP (complexity)In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
, as mentioned above. - Universal second-order logic (excluding existential second-order quantification) yields co-NP.
- Second-orderSO (complexity)Second-order logic is an extenstion of first-order with second orders quantifiers, hence the reader should first read FO to be able to understand this article. In descriptive complexity we can see that the languages recognised by SO formulae is exactly equal to the language decided by a Turing...
logic corresponds to PH. - Second-order logic with a transitive closureTransitive closureIn mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
(commutative or not) yields PSPACEPSPACEIn computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :...
, the problems solvable in polynomial space. - Second-order logic with a least fixed pointLeast fixed pointIn order theory, a branch of mathematics, the least fixed point of a function is the fixed point which is less than or equal to all other fixed points, according to some partial order....
operator gives EXPTIMEEXPTIMEIn computational complexity theory, the complexity class EXPTIME is the set of all decision problems solvable by a deterministic Turing machine in O time, where p is a polynomial function of n....
, the problems solvable in exponential time. -
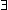HOHO (complexity)High-order logic is an extension of first-order and second-order with high order quantifiers. In descriptive complexity we can see that it is equal to the ELEMENTARY functions...
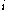, logic with existential quantifier of order 
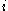followed by a formula of order 
is equal to NTIMENTIMEIn computational complexity theory, the complexity class NTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time O, and unlimited space....
(
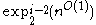) - HOHO (complexity)High-order logic is an extension of first-order and second-order with high order quantifiers. In descriptive complexity we can see that it is equal to the ELEMENTARY functions...
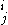=NTIMENTIMEIn computational complexity theory, the complexity class NTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time O, and unlimited space....
(
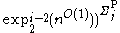
- HOHO (complexity)High-order logic is an extension of first-order and second-order with high order quantifiers. In descriptive complexity we can see that it is equal to the ELEMENTARY functions...
is equal to ELEMENTARY
More precise definitions of those classes can be found on the articles SO
SO (complexity)
Second-order logic is an extenstion of first-order with second orders quantifiers, hence the reader should first read FO to be able to understand this article. In descriptive complexity we can see that the languages recognised by SO formulae is exactly equal to the language decided by a Turing...
and FO
FO (complexity)
FO is the complexity class of structures which can be recognised by formulae of first-order logic. It is the foundation of the field of descriptive complexity and is equal to the complexity class AC0 FO-regular...
.
Further reading
- Shawn Hedman, A first course in logic: an introduction to model theory, proof theory, computability, and complexity, Oxford University Press, 2004, ISBN 0198529813, section 10.3 is a suitable introduction for undergraduates
External links
- Neil Immerman's descriptive complexity page, including a diagram