
HO (complexity)
Encyclopedia
High-order logic is an extension of first-order
and second-order
with high order quantifiers. In descriptive complexity
we can see that it is equal to the ELEMENTARY functions. There is a relation between the th order and non determinist algorithm the time of which is with
th order and non determinist algorithm the time of which is with  level of exponentials.
level of exponentials.
 has got an arity
has got an arity  and represent any subset of the
and represent any subset of the  -tuple
-tuple
of elements of order . They are usually written in upper-case and with a natural number as exponent to indicate the order. High order logic is the set of FO
. They are usually written in upper-case and with a natural number as exponent to indicate the order. High order logic is the set of FO
formulae where we add quantification over second-order variables, hence we will use the terms defined in the FO
article without defining them again.
HO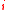 is the set of formulae where variable's order are at most
is the set of formulae where variable's order are at most  . HO
. HO is the subset of the formulae of the form
is the subset of the formulae of the form 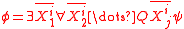 where
where  is a quantifier,
is a quantifier, 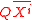 means that
means that 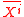 is a tuple of variable of order
is a tuple of variable of order  with the same quantification. So it is the set of formulae with
with the same quantification. So it is the set of formulae with 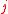 alternations of quantifiers of
alternations of quantifiers of  th order, beginning by and
th order, beginning by and 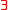 , followed by a formula of order
, followed by a formula of order  .
.
Using the tetration's standard notation,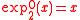 and
and 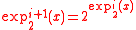 .
. 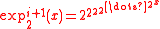 with
with  times
times 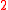
 th order is equivalent to a formula in prenex normal form, where we first write quantification over variable of
th order is equivalent to a formula in prenex normal form, where we first write quantification over variable of  th order and then a formula of order
th order and then a formula of order  in normal form.
in normal form.
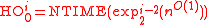 , it means a tower of
, it means a tower of  2, ending with
2, ending with 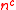 where
where  is a constant. A special case of it is that
is a constant. A special case of it is that 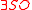 HO
HO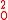 =NTIME(
=NTIME(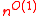 )=NP
)=NP
, which is exactly the Fagin's theorem
. Using oracle machine
s in the polynomial hierarchy
, HO =NTIME
=NTIME
(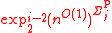 )
)
FO (complexity)
FO is the complexity class of structures which can be recognised by formulae of first-order logic. It is the foundation of the field of descriptive complexity and is equal to the complexity class AC0 FO-regular...
and second-order
SO (complexity)
Second-order logic is an extenstion of first-order with second orders quantifiers, hence the reader should first read FO to be able to understand this article. In descriptive complexity we can see that the languages recognised by SO formulae is exactly equal to the language decided by a Turing...
with high order quantifiers. In descriptive complexity
Descriptive complexity
Descriptive complexity is a branch of computational complexity theory and of finite model theory that characterizes complexity classes by the type of logic needed to express the languages in them. For example, PH, the union of all complexity classes in the polynomial hierarchy, is precisely the...
we can see that it is equal to the ELEMENTARY functions. There is a relation between the
 th order and non determinist algorithm the time of which is with
th order and non determinist algorithm the time of which is with  level of exponentials.
level of exponentials.Definitions and notations
We define high-order variable, a variable of order has got an arity
has got an arity  and represent any subset of the
and represent any subset of the  -tuple
-tupleTuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
of elements of order
 . They are usually written in upper-case and with a natural number as exponent to indicate the order. High order logic is the set of FO
. They are usually written in upper-case and with a natural number as exponent to indicate the order. High order logic is the set of FOFO (complexity)
FO is the complexity class of structures which can be recognised by formulae of first-order logic. It is the foundation of the field of descriptive complexity and is equal to the complexity class AC0 FO-regular...
formulae where we add quantification over second-order variables, hence we will use the terms defined in the FO
FO (complexity)
FO is the complexity class of structures which can be recognised by formulae of first-order logic. It is the foundation of the field of descriptive complexity and is equal to the complexity class AC0 FO-regular...
article without defining them again.
HO
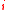 is the set of formulae where variable's order are at most
is the set of formulae where variable's order are at most  . HO
. HO is the subset of the formulae of the form
is the subset of the formulae of the form 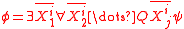 where
where  is a quantifier,
is a quantifier, 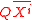 means that
means that 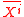 is a tuple of variable of order
is a tuple of variable of order  with the same quantification. So it is the set of formulae with
with the same quantification. So it is the set of formulae with 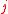 alternations of quantifiers of
alternations of quantifiers of  th order, beginning by and
th order, beginning by and 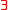 , followed by a formula of order
, followed by a formula of order  .
.Using the tetration's standard notation,
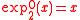 and
and 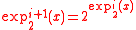 .
. 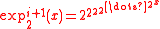 with
with  times
times 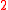
Normal form
Every formula of th order is equivalent to a formula in prenex normal form, where we first write quantification over variable of
th order is equivalent to a formula in prenex normal form, where we first write quantification over variable of  th order and then a formula of order
th order and then a formula of order  in normal form.
in normal form.Relation to complexity classes
HO is equal to ELEMENTARY functions. To be more precise,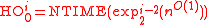 , it means a tower of
, it means a tower of  2, ending with
2, ending with 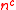 where
where  is a constant. A special case of it is that
is a constant. A special case of it is that 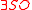 HO
HO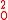 =NTIME(
=NTIME(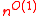 )=NP
)=NPNP
-Locations:* NP postcode area, Newport, United Kingdom* NP, country code for Nepal ** .np, the country code top level domain for Nepal* NP, anabbreviation for Ngee Ann Polytechnic, Singapore...
, which is exactly the Fagin's theorem
Fagin's theorem
Fagin's theorem is a result in descriptive complexity theory that states that the set of all properties expressible in existential second-order logic is precisely the complexity class NP...
. Using oracle machine
Oracle machine
In complexity theory and computability theory, an oracle machine is an abstract machine used to study decision problems. It can be visualized as a Turing machine with a black box, called an oracle, which is able to decide certain decision problems in a single operation. The problem can be of any...
s in the polynomial hierarchy
Polynomial hierarchy
In computational complexity theory, the polynomial hierarchy is a hierarchy of complexity classes that generalize the classes P, NP and co-NP to oracle machines...
, HO
 =NTIME
=NTIMENTIME
In computational complexity theory, the complexity class NTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time O, and unlimited space....
(
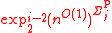 )
)

