
SO (complexity)
Encyclopedia
Second-order logic is an extenstion of first-order
with second orders quantifiers, hence the reader should first read FO (complexity)
to be able to understand this article. In descriptive complexity
we can see that the languages recognised by SO formulae is exactly equal to the language decided by a Turing machine
in the polynomial hierarchy. Extensions of SO with some operators also give us the same expressivity than some well known complexity class
., so it is a way to do proofs about the complexity of some problems without having to go to the algorithm
ic level.
 and represent any proposition of arity
and represent any proposition of arity  , i.e. a subset of the t-tuples of the universe. They are usually written in upper-case. Second order logic is the set of FO
, i.e. a subset of the t-tuples of the universe. They are usually written in upper-case. Second order logic is the set of FO
formulae where we add quantification over second-order variables, hence we will use the terms defined in the FO
article without defining them again.
This means that SO with only existential second-order quantification is equal to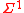 which is NP
which is NP
, and with only universal quantification is equal to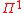 which is Co-NP.
which is Co-NP.
such that the first order quantifiers are all universal and the quantifier-free part of the formula is in Horn
form, which means that it is a big AND of OR, and in each "OR" every variable except possibly one are negated.
This class is equal to P
.
Those formulaes can be made in prenex form where the second order is existential and the first order universal without loss of generalities.
This class is equal to NL
.
Those formulaes can be made in prenex form where the second order is existential and the first order universal without loss of generalities.
. The TC operator can now also take second-order variable as argument. SO[TC] is equal to PSPACE.
. The LFP operator can now also take second-order variable as argument. SO(LFP) is equal to EXPTIME
.
. But we now also have second-order quantifier in the quantifier block. It is known that:
FO (complexity)
FO is the complexity class of structures which can be recognised by formulae of first-order logic. It is the foundation of the field of descriptive complexity and is equal to the complexity class AC0 FO-regular...
with second orders quantifiers, hence the reader should first read FO (complexity)
FO (complexity)
FO is the complexity class of structures which can be recognised by formulae of first-order logic. It is the foundation of the field of descriptive complexity and is equal to the complexity class AC0 FO-regular...
to be able to understand this article. In descriptive complexity
Descriptive complexity
Descriptive complexity is a branch of computational complexity theory and of finite model theory that characterizes complexity classes by the type of logic needed to express the languages in them. For example, PH, the union of all complexity classes in the polynomial hierarchy, is precisely the...
we can see that the languages recognised by SO formulae is exactly equal to the language decided by a Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
in the polynomial hierarchy. Extensions of SO with some operators also give us the same expressivity than some well known complexity class
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
., so it is a way to do proofs about the complexity of some problems without having to go to the algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
ic level.
Definition and examples
We define second-order variable, a SO variable has got an arity and represent any proposition of arity
and represent any proposition of arity  , i.e. a subset of the t-tuples of the universe. They are usually written in upper-case. Second order logic is the set of FO
, i.e. a subset of the t-tuples of the universe. They are usually written in upper-case. Second order logic is the set of FOFO (complexity)
FO is the complexity class of structures which can be recognised by formulae of first-order logic. It is the foundation of the field of descriptive complexity and is equal to the complexity class AC0 FO-regular...
formulae where we add quantification over second-order variables, hence we will use the terms defined in the FO
FO (complexity)
FO is the complexity class of structures which can be recognised by formulae of first-order logic. It is the foundation of the field of descriptive complexity and is equal to the complexity class AC0 FO-regular...
article without defining them again.
Normal form
Every formula is equivalent to a formula in prenex normal form, where we first write quantification on variable on second order and then a FO-formula in prenex normal form.Relation to complexity classes
SO is equal to PH, more precisely we have that formula in prenex normal form where existential and universal of second order alternate k times are the kth level of the polynomial hierarchy.This means that SO with only existential second-order quantification is equal to
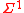 which is NP
which is NPNP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
, and with only universal quantification is equal to
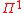 which is Co-NP.
which is Co-NP.Horn formulae are equal to P
SO(horn) is the set of boolean queries definable with SO formulae in disjunctive normal formDisjunctive normal form
In boolean logic, a disjunctive normal form is a standardization of a logical formula which is a disjunction of conjunctive clauses. As a normal form, it is useful in automated theorem proving. A logical formula is considered to be in DNF if and only if it is a disjunction of one or more...
such that the first order quantifiers are all universal and the quantifier-free part of the formula is in Horn
Horn clause
In mathematical logic, a Horn clause is a clause with at most one positive literal. They are named after the logician Alfred Horn, who first pointed out the significance of such clauses in 1951...
form, which means that it is a big AND of OR, and in each "OR" every variable except possibly one are negated.
This class is equal to P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
.
Those formulaes can be made in prenex form where the second order is existential and the first order universal without loss of generalities.
Krom formulae are equal to NL
SO(Krom) is the set of boolean queries definable with second-order formulae in conjunctive normal form such that the first order quantifiers are universal and the quantifier-free part of the formula is in Krom form, which means that the first order formula is a big AND of OR, and in each "OR" there is at most two variables.This class is equal to NL
NL (complexity)
In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space....
.
Those formulaes can be made in prenex form where the second order is existential and the first order universal without loss of generalities.
Transitive closure is PSPACE
SO(tc) is to SO what FO(TC) is to FOFO (complexity)
FO is the complexity class of structures which can be recognised by formulae of first-order logic. It is the foundation of the field of descriptive complexity and is equal to the complexity class AC0 FO-regular...
. The TC operator can now also take second-order variable as argument. SO[TC] is equal to PSPACE.
Least fixed point is EXPTIME
SO[LFP] is to SO what FO(LFP) is to FOFO (complexity)
FO is the complexity class of structures which can be recognised by formulae of first-order logic. It is the foundation of the field of descriptive complexity and is equal to the complexity class AC0 FO-regular...
. The LFP operator can now also take second-order variable as argument. SO(LFP) is equal to EXPTIME
EXPTIME
In computational complexity theory, the complexity class EXPTIME is the set of all decision problems solvable by a deterministic Turing machine in O time, where p is a polynomial function of n....
.
Iterating
SO(t(n)) is to SO what FO[t(n)] is to FOFO (complexity)
FO is the complexity class of structures which can be recognised by formulae of first-order logic. It is the foundation of the field of descriptive complexity and is equal to the complexity class AC0 FO-regular...
. But we now also have second-order quantifier in the quantifier block. It is known that:
- SO[
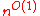 ] is equal to SPACESPACEThe term SPACE can refer to:* SPACE, a Canadian science-fiction channel* The Society for Promotion of Alternative Computing and Employment* DSPACE, a term in computational complexity theory...
] is equal to SPACESPACEThe term SPACE can refer to:* SPACE, a Canadian science-fiction channel* The Society for Promotion of Alternative Computing and Employment* DSPACE, a term in computational complexity theory...
it is also another way to write SO(TC). - SO[
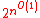 ] is equal to EXPTIMEEXPTIMEIn computational complexity theory, the complexity class EXPTIME is the set of all decision problems solvable by a deterministic Turing machine in O time, where p is a polynomial function of n....
] is equal to EXPTIMEEXPTIMEIn computational complexity theory, the complexity class EXPTIME is the set of all decision problems solvable by a deterministic Turing machine in O time, where p is a polynomial function of n....
it is also another way to write SO(LFP)
Externals links
- Complexity zoo about SO, see the class under it also.

