Diagonalizable group
Encyclopedia
In mathematics, an affine group
is said to be diagonalizable if it is isomorphic to a subgroup of Dn, the group of diagonal matrices. A diagonalizable group defined over k is said to split over k or k-split if the isomorphism is defined over k. This coincides with the usual notion of split
for an algebraic group. Every diagonalizable group splits over ks. Any closed subgroup and image of diagonalizable groups are diagonalizable. The torsion subgroup
of a diagonalizable group is dense.
The category of diagonalizable groups defined over k is equivalent to the category of finitely generated abelian group with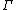
-equivariant morphisms without p-torsion. This is an analog of Poincaré duality
and motivated the terminology.
A diagonalizable k-group is said to be anisotropic if it has no nontrivial k-valued character.
The so-called "rigidity" states that the identity component of the centralizer of a diagonalizable group coincides with the identity component of the normalizer of the group. The fact plays a crucial role in the structure theory of solvable groups.
A connected diagonalizable group is called an algebraic torus
(which is not necessarily compact, in contrast to a complex torus
). A k-torus is a torus defined over k. The centralizer of a maximal torus is called a Cartan subgroup
.
Affine group
In mathematics, the affine group or general affine group of any affine space over a field K is the group of all invertible affine transformations from the space into itself.It is a Lie group if K is the real or complex field or quaternions....
is said to be diagonalizable if it is isomorphic to a subgroup of Dn, the group of diagonal matrices. A diagonalizable group defined over k is said to split over k or k-split if the isomorphism is defined over k. This coincides with the usual notion of split
Splitting lemma
In mathematics, and more specifically in homological algebra, the splitting lemma states that in any abelian category, the following statements for short exact sequence are equivalent....
for an algebraic group. Every diagonalizable group splits over ks. Any closed subgroup and image of diagonalizable groups are diagonalizable. The torsion subgroup
Torsion subgroup
In the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...
of a diagonalizable group is dense.
The category of diagonalizable groups defined over k is equivalent to the category of finitely generated abelian group with
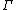-equivariant morphisms without p-torsion. This is an analog of Poincaré dualityPoincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
and motivated the terminology.
A diagonalizable k-group is said to be anisotropic if it has no nontrivial k-valued character.
The so-called "rigidity" states that the identity component of the centralizer of a diagonalizable group coincides with the identity component of the normalizer of the group. The fact plays a crucial role in the structure theory of solvable groups.
A connected diagonalizable group is called an algebraic torus
Algebraic torus
In mathematics, an algebraic torus is a type of commutative affine algebraic group. These groups were named by analogy with the theory of tori in Lie group theory...
(which is not necessarily compact, in contrast to a complex torus
Complex torus
In mathematics, a complex torus is a particular kind of complex manifold M whose underlying smooth manifold is a torus in the usual sense...
). A k-torus is a torus defined over k. The centralizer of a maximal torus is called a Cartan subgroup
Cartan subgroup
In mathematics, a Cartan subgroup of a Lie group or algebraic group G is one of the subgroups whose Lie algebrais a Cartan subalgebra. The dimension of a Cartan subgroup, and therefore of a Cartan subalgebra, is the rank of G.-Conventions:...
.