
Difference polynomials
Encyclopedia
In mathematics
, in the area of complex analysis
, the general difference polynomials are a polynomial sequence
, a certain subclass of the Sheffer polynomials, which include the Newton polynomial
s, Selberg's polynomials, and the Stirling interpolation polynomials as special cases.
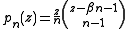
where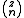 is the binomial coefficient
is the binomial coefficient
. For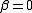 , the generated polynomials
, the generated polynomials  are the Newton polynomials
are the Newton polynomials
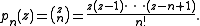
The case of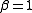 generates Selberg's polynomials, and the case of
generates Selberg's polynomials, and the case of 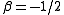 generates Stirling's interpolation polynomials.
generates Stirling's interpolation polynomials.
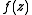 , define the moving difference of f as
, define the moving difference of f as

where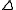 is the forward difference operator. Then, provided that f obeys certain summability conditions, then it may be represented in terms of these polynomials as
is the forward difference operator. Then, provided that f obeys certain summability conditions, then it may be represented in terms of these polynomials as
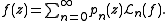
The conditions for summability (that is, convergence) for this sequence is a fairly complex topic; in general, one may say that a necessary condition is that the analytic function be of less than exponential type. Summability conditions are discussed in detail in Boas & Buck.
for the general difference polynomials is given by
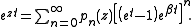
This generating function can be brought into the form of the generalized Appell representation

by setting ,
, 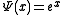 ,
, 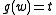 and
and  .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the area of complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, the general difference polynomials are a polynomial sequence
Polynomial sequence
In mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
, a certain subclass of the Sheffer polynomials, which include the Newton polynomial
Newton polynomial
In the mathematical field of numerical analysis, a Newton polynomial, named after its inventor Isaac Newton, is the interpolation polynomial for a given set of data points in the Newton form...
s, Selberg's polynomials, and the Stirling interpolation polynomials as special cases.
Definition
The general difference polynomial sequence is given by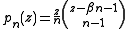
where
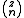 is the binomial coefficient
is the binomial coefficientBinomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
. For
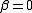 , the generated polynomials
, the generated polynomials  are the Newton polynomials
are the Newton polynomials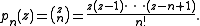
The case of
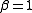 generates Selberg's polynomials, and the case of
generates Selberg's polynomials, and the case of 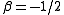 generates Stirling's interpolation polynomials.
generates Stirling's interpolation polynomials.Moving differences
Given an analytic functionAnalytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
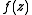 , define the moving difference of f as
, define the moving difference of f as
where
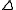 is the forward difference operator. Then, provided that f obeys certain summability conditions, then it may be represented in terms of these polynomials as
is the forward difference operator. Then, provided that f obeys certain summability conditions, then it may be represented in terms of these polynomials as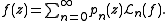
The conditions for summability (that is, convergence) for this sequence is a fairly complex topic; in general, one may say that a necessary condition is that the analytic function be of less than exponential type. Summability conditions are discussed in detail in Boas & Buck.
Generating function
The generating functionGenerating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
for the general difference polynomials is given by
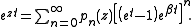
This generating function can be brought into the form of the generalized Appell representation

by setting
 ,
, 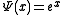 ,
, 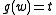 and
and  .
.

