
Exponential type
Encyclopedia
In complex analysis
, a branch of mathematics, an entire function
function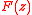 is said to be of exponential type
is said to be of exponential type  if for every
if for every  there exists a constant
there exists a constant 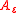 such that
such that
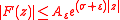
for every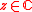 .
.
We say is of exponential type if
is of exponential type if 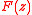 is of exponential type
is of exponential type  for some
for some  . The number
. The number
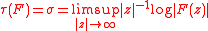
is the exponential type of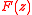 .
.
s of several complex variables
.
Suppose is a convex
is a convex
, compact
, and symmetric subset of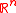 . It is known that for every such
. It is known that for every such  there is an associated norm
there is an associated norm
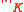 with the property that
with the property that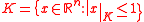 .
.
In other words, is the unit ball in
is the unit ball in 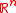 with respect to
with respect to  .
.
The set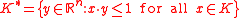
is called the polar set and is also a convex
, compact
, and symmetric subset of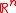 . Furthermore, we can write
. Furthermore, we can write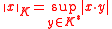 .
.
We extend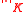 from
from 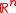 to
to 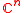 by
by
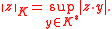
An entire function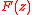 of
of  -complex variables is said to be of exponential type with respect to
-complex variables is said to be of exponential type with respect to  if for every
if for every  there exists a constant
there exists a constant 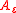 such that
such that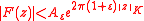
for all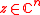 .
.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a branch of mathematics, an entire function
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
function
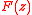 is said to be of exponential type
is said to be of exponential type  if for every
if for every  there exists a constant
there exists a constant 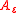 such that
such that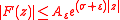
for every
 .
.We say
 is of exponential type if
is of exponential type if  is of exponential type
is of exponential type  for some
for some  . The number
. The number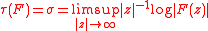
is the exponential type of
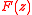 .
.Exponential type with respect to a symmetric convex body
has given a generalization of exponential type for entire functionEntire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
s of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
.
Suppose
 is a convex
is a convexConvex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
, compact
Compact element
In the mathematical area of order theory, the compact or finite elements of a partially ordered set are those elements that cannot be subsumed by a supremum of any non-empty directed set that does not already contain members above the compact element....
, and symmetric subset of
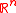 . It is known that for every such
. It is known that for every such  there is an associated norm
there is an associated normNorm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
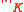 with the property that
with the property that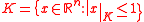 .
.In other words,
 is the unit ball in
is the unit ball in 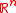 with respect to
with respect to  .
.The set
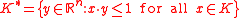
is called the polar set and is also a convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
, compact
Compact element
In the mathematical area of order theory, the compact or finite elements of a partially ordered set are those elements that cannot be subsumed by a supremum of any non-empty directed set that does not already contain members above the compact element....
, and symmetric subset of
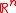 . Furthermore, we can write
. Furthermore, we can write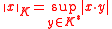 .
.We extend
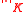 from
from 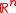 to
to 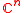 by
by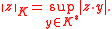
An entire function
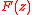 of
of  -complex variables is said to be of exponential type with respect to
-complex variables is said to be of exponential type with respect to  if for every
if for every  there exists a constant
there exists a constant 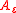 such that
such that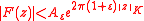
for all
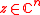 .
.

