.gif)
Dilation (morphology)
Encyclopedia
Dilation is one of the basic operations in mathematical morphology
. Originally developed for binary images, it has been expanded first to grayscale
images, and then to complete lattices. The dilation operation usually uses a structuring element
for probing and expanding the shapes contained in the input image.
In binary morphology, dilation is a shift-invariant (translation invariant) operator, strongly related to the Minkowski addition
.
A binary image is viewed in mathematical morphology as a subset
of an Euclidean space
Rd or the integer grid Zd, for some dimension d. Let E be a Euclidean space or an integer grid, A a binary image in E, and B a structuring element.
The dilation of A by B is defined by:
The dilation is commutative, also given by: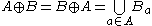
.
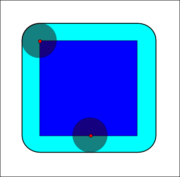
If B has a center on the origin, then the dilation of A by B can be understood as the locus of the points covered by B when the center of B moves inside A. The dilation of a square of side 10, centered at the origin, by a disk of radius 2, also centered at the origin, is a square of side 14, with rounded corners, centered at the origin. The radius of the rounded corners is 2.
The dilation can also be obtained by: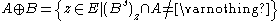
, where Bs denotes the symmetric
of B, that is,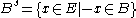
.
morphology, images are functions
mapping a Euclidean space
or grid
E into
, where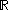 
is the set of reals, 
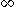is an element larger than any real number, and 
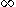is an element smaller than any real number.
Grayscale structuring elements are also functions of the same format, called "structuring functions".
Denoting an image by f(x) and the structuring function by b(x), the grayscale dilation of f by b is given by
where "sup" denotes the supremum
.
where
.
In this case, the dilation is greatly simplified, and given by
In the bounded, discrete case (E is a grid and B is bounded), the supremum
operator can be replaced by the maximum. Thus, dilation is a particular case of order statistics filters, returning the maximum value within a moving window (the symmetric of the structuring function support B).
s are partially ordered set
s, where every subset has an infimum
and a supremum
. In particular, it contains a least element and a greatest element
(also denoted "universe").
Let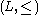
be a complete lattice, with infimum and minimum symbolized by 
and 
, respectively. Its universe and least element are symbolized by U and 
, respectively. Moreover, let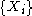 
be a collection of elements from L.
A dilation is any operator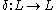
that distributes over the supremum, and preserves the least element. I.e.:
Mathematical morphology
Mathematical morphology is a theory and technique for the analysis and processing of geometrical structures, based on set theory, lattice theory, topology, and random functions...
. Originally developed for binary images, it has been expanded first to grayscale
Grayscale
In photography and computing, a grayscale or greyscale digital image is an image in which the value of each pixel is a single sample, that is, it carries only intensity information...
images, and then to complete lattices. The dilation operation usually uses a structuring element
Structuring element
In mathematical morphology, a structuring element is a shape, used to probe or interact with a given image, with the purpose of drawing conclusions on how this shape fits or misses the shapes in the image...
for probing and expanding the shapes contained in the input image.
Binary Operator
Minkowski addition
In geometry, the Minkowski sum of two sets A and B in Euclidean space is the result of adding every element of A to every element of B, i.e...
.
A binary image is viewed in mathematical morphology as a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of an Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rd or the integer grid Zd, for some dimension d. Let E be a Euclidean space or an integer grid, A a binary image in E, and B a structuring element.
The dilation of A by B is defined by:
-
.
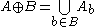The dilation is commutative, also given by:
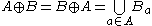.If B has a center on the origin, then the dilation of A by B can be understood as the locus of the points covered by B when the center of B moves inside A. The dilation of a square of side 10, centered at the origin, by a disk of radius 2, also centered at the origin, is a square of side 14, with rounded corners, centered at the origin. The radius of the rounded corners is 2.
The dilation can also be obtained by:
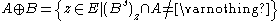, where Bs denotes the symmetricRotational symmetry
Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
of B, that is,
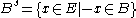.Properties of binary dilation
Here are some properties of the binary dilation operator:- It is translation invariant.
- It is increasing, that is, if
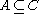, then 
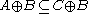. - It is commutative.
- If the origin of E belongs to the structuring element B, then it is extensive, i.e.,
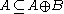. - It is associative, i.e.,
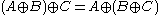. - It is distributive over set union
Grayscale dilation
In grayscaleGrayscale
In photography and computing, a grayscale or greyscale digital image is an image in which the value of each pixel is a single sample, that is, it carries only intensity information...
morphology, images are functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
mapping a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
or grid
Lattice graph
The terms lattice graph, mesh graph, or grid graph refer to a number of categories of graphs whose drawing corresponds to some grid/mesh/lattice, i.e., its vertices correspond to the nodes of the mesh and its edges correspond to the ties between the nodes.-Square grid graph:A common type of a...
E into
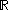, where is the set of reals, 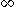is an element larger than any real number, and is an element smaller than any real number.Grayscale structuring elements are also functions of the same format, called "structuring functions".
Denoting an image by f(x) and the structuring function by b(x), the grayscale dilation of f by b is given by
-
,
where "sup" denotes the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
.
Flat structuring functions
It is common to use flat structuring elements in morphological applications. Flat structuring functions are functions b(x) in the form-
,
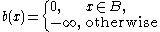where
.In this case, the dilation is greatly simplified, and given by
-
.
In the bounded, discrete case (E is a grid and B is bounded), the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
operator can be replaced by the maximum. Thus, dilation is a particular case of order statistics filters, returning the maximum value within a moving window (the symmetric of the structuring function support B).
Dilation on complete lattices
Complete latticeComplete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
s are partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
s, where every subset has an infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
and a supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
. In particular, it contains a least element and a greatest element
Greatest element
In mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...
(also denoted "universe").
Let
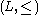be a complete lattice, with infimum and minimum symbolized by and , respectively. Its universe and least element are symbolized by U and , respectively. Moreover, let 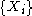be a collection of elements from L.A dilation is any operator
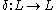that distributes over the supremum, and preserves the least element. I.e.:
-
, -
.
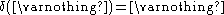See also
- Mathematical morphologyMathematical morphologyMathematical morphology is a theory and technique for the analysis and processing of geometrical structures, based on set theory, lattice theory, topology, and random functions...
- ClosingClosing (morphology)In mathematical morphology, the closing of a set A by a structuring element B is the erosion of the dilation of that set,A\bullet B = \ominus B, \, where \oplus and \ominus denote the dilation and erosion, respectively....
- ErosionErosion (morphology)For use of "Erosion" in dermatopathology, see Erosion Erosion is one of two fundamental operations in Morphological image processing from which all other morphological operations are based...
- OpeningOpening (morphology)In mathematical morphology, opening is the dilation of the erosion of a set A by a structuring element B:A\circ B = \oplus B, \, where \ominus and \oplus denote erosion and dilation, respectively....