Mathematical morphology - AbsoluteAstronomy.com

Mathematical morphology (MM) is a theory and technique for the analysis and processing of geometrical structures, based on set theory

Set theory

Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...

, lattice theory, topology

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

, and random function

Random function

A random function is a function chosen at random from a finite family of functions. Typically, the family consists of the set of all maps from the domain to the codomain. Thus, a random function can be considered to map each input independently at random to any one of the possible outputs. Viewed...

s. MM is most commonly applied to digital image

Digital image

A digital image is a numeric representation of a two-dimensional image. Depending on whether or not the image resolution is fixed, it may be of vector or raster type...

s, but it can be employed as well on graphs

Graph (mathematics)

In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

, surface meshes

Polygon mesh

A polygon mesh or unstructured grid is a collection of vertices, edges and faces that defines the shape of a polyhedral object in 3D computer graphics and solid modeling...

, solids

Solid geometry

In mathematics, solid geometry was the traditional name for the geometry of three-dimensional Euclidean space — for practical purposes the kind of space we live in. It was developed following the development of plane geometry...

, and many other spatial structures.

Topological

Topology

and geometrical

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

continuous

Continuum (theory)

Continuum theories or models explain variation as involving a gradual quantitative transition without abrupt changes or discontinuities. It can be contrasted with 'categorical' models which propose qualitatively different states.-In physics:...

-space concepts such as size

Size

The word size may refer to how big something is. In particular:* Measurement, the process or the result of determining the magnitude of a quantity, such as length or mass, relative to a unit of measurement, such as a meter or a kilogram...

, shape

Shape

The shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...

, convexity

Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

, connectivity

Connectedness

In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...

, and geodesic distance, can be characterized by MM on both continuous and discrete space

Discrete space

In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...

s. MM is also the foundation of morphological image processing, which consists of a set of operators that transform images according to the above characterizations.

MM was originally developed for binary image

Binary image

A binary image is a digital image that has only two possible values for each pixel. Typically the two colors used for a binary image are black and white though any two colors can be used. The color used for the object in the image is the foreground color while the rest of the image is the...

s, and was later extended to grayscale

Grayscale

In photography and computing, a grayscale or greyscale digital image is an image in which the value of each pixel is a single sample, that is, it carries only intensity information...

functions

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

and images. The subsequent generalization to complete lattice

Complete lattice

In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...

s is widely accepted today as MM's theoretical foundation.

History

Mathematical Morphology was born in 1964 from the collaborative work of Georges Matheron

Georges Matheron

Georges François Paul Marie Matheron was a French mathematician and geologist, known as the founder of geostatistics and a co-founder of mathematical morphology. In 1968 he created the Centre de Géostatistique et de Morphologie Mathématique at the Paris School of Mines in Fontainebleau...

and Jean Serra

Jean Serra

Jean Paul Frédéric Serra is a French mathematician and engineer, and known as one of the co-founders of mathematical morphology.-Education:...

, at the École des Mines de Paris, France

France

The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...

. Matheron supervised the PhD

PHD

PHD may refer to:*Ph.D., a doctorate of philosophy*Ph.D. , a 1980s British group*PHD finger, a protein sequence*PHD Mountain Software, an outdoor clothing and equipment company*PhD Docbook renderer, an XML renderer...

thesis

Thesis

A dissertation or thesis is a document submitted in support of candidature for an academic degree or professional qualification presenting the author's research and findings...

of Serra, devoted to the quantification of mineral characteristics from thin cross section

Cross section (geometry)

In geometry, a cross-section is the intersection of a figure in 2-dimensional space with a line, or of a body in 3-dimensional space with a plane, etc...

s, and this work resulted in a novel practical approach, as well as theoretical advancements in integral geometry

Integral geometry

In mathematics, integral geometry is the theory of measures on a geometrical space invariant under the symmetry group of that space. In more recent times, the meaning has been broadened to include a view of invariant transformations from the space of functions on one geometrical space to the...

and topology

Topology

.

In 1968, the Centre de Morphologie Mathématique
Centre de Morphologie Mathématique
Centre de Morphologie Mathématique is a research center of the École des Mines de Paris, France, devoted to the research and promotion of mathematical morphology...

was founded by the École des Mines de Paris in Fontainebleau

Fontainebleau

Fontainebleau is a commune in the metropolitan area of Paris, France. It is located south-southeast of the centre of Paris. Fontainebleau is a sub-prefecture of the Seine-et-Marne department, and it is the seat of the arrondissement of Fontainebleau...

, France, led by Matheron and Serra.

During the rest of the 1960s and most of the 1970s, MM dealt essentially with binary image

Binary image

s, treated as sets, and generated a large number of binary operators and techniques: Hit-or-miss transform

Hit-or-miss transform

In mathematical morphology, hit-or-miss transform is an operation that detects a given configuration in a binary image, using the morphological erosion operator and a pair of disjoint structuring elements...

, dilation

Dilation (morphology)

Dilation is one of the basic operations in mathematical morphology. Originally developed for binary images, it has been expanded first to grayscale images, and then to complete lattices...

, erosion

Erosion (morphology)

For use of "Erosion" in dermatopathology, see Erosion Erosion is one of two fundamental operations in Morphological image processing from which all other morphological operations are based...

, opening

Opening (morphology)

In mathematical morphology, opening is the dilation of the erosion of a set A by a structuring element B:A\circ B = \oplus B, \, where \ominus and \oplus denote erosion and dilation, respectively....

, closing

Closing (morphology)

In mathematical morphology, the closing of a set A by a structuring element B is the erosion of the dilation of that set,A\bullet B = \ominus B, \, where \oplus and \ominus denote the dilation and erosion, respectively....

, granulometry

Granulometry (morphology)

In mathematical morphology, granulometry is an approach to compute a size distribution of grains in binary images, using a series of morphological opening operations...

, thinning, skeletonization

Topological skeleton

In shape analysis, skeleton of a shape is a thin version of that shape that is equidistant to its boundaries. The skeleton usually emphasizes geometrical and topological properties of the shape, such as its connectivity, topology, length, direction, and width...

, ultimate erosion, conditional bisector, and others. A random approach was also developed, based on novel image models. Most of the work in that period was developed in Fontainebleau.

From mid-1970s to mid-1980s, MM was generalized to grayscale

Grayscale

In photography and computing, a grayscale or greyscale digital image is an image in which the value of each pixel is a single sample, that is, it carries only intensity information...

functions and image

Image

An image is an artifact, for example a two-dimensional picture, that has a similar appearance to some subject—usually a physical object or a person.-Characteristics:...

s as well. Besides extending the main concepts (such as dilation, erosion, etc...) to functions, this generalization yielded new operators, such as morphological gradients

Morphological Gradient

In mathematical morphology and digital image processing, a morphological gradient is the difference between the dilation and the erosion of a given image. It is an image where each pixel value indicates the contrast intensity in the close neighborhood of that pixel...

, top-hat transform

Top-hat transform

In mathematical morphology and digital image processing, top-hat transform is an operation that extracts small elements and details from given images...

and the Watershed

Watershed (algorithm)

A grey-level image may be seen as a topographic relief, where the grey level of a pixel is interpreted as its altitude in the relief.A drop of water falling on a topographic relief flows along a path to finally reach a local minimum...

(MM's main segmentation

Segmentation (image processing)

In computer vision, segmentation refers to the process of partitioning a digital image into multiple segments . The goal of segmentation is to simplify and/or change the representation of an image into something that is more meaningful and easier to analyze...

approach).

In the 1980s and 1990s, MM gained a wider recognition, as research centers in several countries began to adopt and investigate the method. MM started to be applied to a large number of imaging problems and applications.

In 1986, Jean Serra further generalized MM, this time to a theoretical framework based on complete lattice

Complete lattice

s. This generalization brought flexibility to the theory, enabling its application to a much larger number of structures, including color images, video, graphs

Graph (mathematics)

, meshes, etc. At the same time, Matheron and Serra also formulated a theory for morphological filtering

Filter (mathematics)

In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...

, based on the new lattice framework.

The 1990s and 2000s also saw further theoretical advancements, including the concepts of connections and levelings.

In 1993, the first International Symposium on Mathematical Morphology (ISMM) took place in Barcelona

Barcelona

Barcelona is the second largest city in Spain after Madrid, and the capital of Catalonia, with a population of 1,621,537 within its administrative limits on a land area of...

, Spain

Spain

Spain , officially the Kingdom of Spain languages]] under the European Charter for Regional or Minority Languages. In each of these, Spain's official name is as follows:;;;;;;), is a country and member state of the European Union located in southwestern Europe on the Iberian Peninsula...

. Since then, ISMMs are organized every 2–3 years, each time in a different part of the world: Fontainebleau

Fontainebleau

, France

France

(1994); Atlanta, USA (1996); Amsterdam

Amsterdam

Amsterdam is the largest city and the capital of the Netherlands. The current position of Amsterdam as capital city of the Kingdom of the Netherlands is governed by the constitution of August 24, 1815 and its successors. Amsterdam has a population of 783,364 within city limits, an urban population...

, Netherlands

Netherlands

The Netherlands is a constituent country of the Kingdom of the Netherlands, located mainly in North-West Europe and with several islands in the Caribbean. Mainland Netherlands borders the North Sea to the north and west, Belgium to the south, and Germany to the east, and shares maritime borders...

(1998); Palo Alto, CA

California

California is a state located on the West Coast of the United States. It is by far the most populous U.S. state, and the third-largest by land area...

, USA (2000); Sydney

Sydney

Sydney is the most populous city in Australia and the state capital of New South Wales. Sydney is located on Australia's south-east coast of the Tasman Sea. As of June 2010, the greater metropolitan area had an approximate population of 4.6 million people...

, Australia

Australia

Australia , officially the Commonwealth of Australia, is a country in the Southern Hemisphere comprising the mainland of the Australian continent, the island of Tasmania, and numerous smaller islands in the Indian and Pacific Oceans. It is the world's sixth-largest country by total area...

(2002); Paris

Paris

Paris is the capital and largest city in France, situated on the river Seine, in northern France, at the heart of the Île-de-France region...

, France

France

(2004); Rio de Janeiro

Rio de Janeiro

Rio de Janeiro , commonly referred to simply as Rio, is the capital city of the State of Rio de Janeiro, the second largest city of Brazil, and the third largest metropolitan area and agglomeration in South America, boasting approximately 6.3 million people within the city proper, making it the 6th...

, Brazil

Brazil

Brazil , officially the Federative Republic of Brazil , is the largest country in South America. It is the world's fifth largest country, both by geographical area and by population with over 192 million people...

(2007); Groningen, Netherlands

Netherlands

(2009); and Intra (Verbania

Verbania

Verbania is a city and comune on the shore of Lake Maggiore, Piedmont, in northwest Italy, about north-west of Milan and about from Locarno in Switzerland.-Overview:...

), Italy

Italy

Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...

(2011).

Binary morphology

In binary morphology, an image is viewed as a subset

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

of an Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

or the integer grid

, for some dimension d.

Structuring element

The basic idea in binary morphology is to probe an image with a simple, pre-defined shape, drawing conclusions on how this shape fits or misses the shapes in the image. This simple "probe" is called structuring element

Structuring element

In mathematical morphology, a structuring element is a shape, used to probe or interact with a given image, with the purpose of drawing conclusions on how this shape fits or misses the shapes in the image...

, and is itself a binary image (i.e., a subset of the space or grid).

Here are some examples of widely used structuring elements (denoted by B):

Let ; B is an open disk of radius r, centered at the origin.
Let ; B is a 3x3 square, that is, B={(-1,-1), (-1,0), (-1,1), (0,-1), (0,0), (0,1), (1,-1), (1,0), (1,1)}.
Let ; B is the "cross" given by: B={(-1,0), (0,-1), (0,0), (0,1), (1,0)}.

Basic operators

The basic operations are shift-invariant (translation invariant) operators strongly related to Minkowski addition

Minkowski addition

In geometry, the Minkowski sum of two sets A and B in Euclidean space is the result of adding every element of A to every element of B, i.e...

.

Let E be a Euclidean space or an integer grid, and A a binary image in E.

Erosion

The erosion

Erosion (morphology)

For use of "Erosion" in dermatopathology, see Erosion Erosion is one of two fundamental operations in Morphological image processing from which all other morphological operations are based...

of the binary image A by the structuring element B is defined by:

where B_z is the translation of B by the vector z, i.e.,

.

When the structuring element B has a center (e.g., B is a disk or a square), and this center is located on the origin of E, then the erosion of A by B can be understood as the locus

Locus (mathematics)

In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....

of points reached by the center of B when B moves inside A. For example, the erosion of a square of side 10, centered at the origin, by a disc of radius 2, also centered at the origin, is a square of side 6 centered at the origin.

The erosion of A by B is also given by the expression:

.

Example application: Assume we have received a fax of a dark photocopy. Everything looks like it was written with a pen that is bleeding. Erosion process will allow thicker lines to get skinny and detect the hole inside the letter "o".

Dilation

The dilation

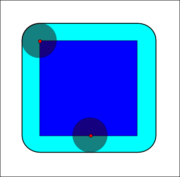
Dilation (morphology)

Dilation is one of the basic operations in mathematical morphology. Originally developed for binary images, it has been expanded first to grayscale images, and then to complete lattices...

of A by the structuring element B is defined by:

The dilation is commutative, also given by:

.

If B has a center on the origin, as before, then the dilation of A by B can be understood as the locus of the points covered by B when the center of B moves inside A. In the above example, the dilation of the square of side 10 by the disk of radius 2 is a square of side 14, with rounded corners, centered at the origin. The radius of the rounded corners is 2.

The dilation can also be obtained by:

, where B^s denotes the symmetric

Rotational symmetry

Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...

of B, that is,

.

Example application: Dilation is the opposite of the erosion. Figures that are very lightly drawn get thick when "dilated". Easiest way to describe it is to imagine the same fax/text is written with a thicker pen.

Opening

The opening

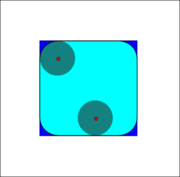
Opening (morphology)

In mathematical morphology, opening is the dilation of the erosion of a set A by a structuring element B:A\circ B = \oplus B, \, where \ominus and \oplus denote erosion and dilation, respectively....

of A by B is obtained by the erosion of A by B, followed by dilation of the resulting image by B:

The opening is also given by

, which means that it is the locus of translations of the structuring element B inside the image A. In the case of the square of side 10, and a disc of radius 2 as the structuring element, the opening is a square of side 10 with rounded corners, where the corner radius is 2.

Example application: Let's assume someone has written a note on a non-soaking paper that writing looks like it is growing tiny hairy roots all over. Opening essentially removes the outer tiny "hairline" leaks and restores the text. The side effect is that it rounds off things. The sharp edges start to disappear.

Closing

The closing

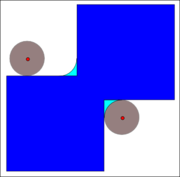
Closing (morphology)

of A by B is obtained by the dilation of A by B, followed by erosion of the resulting structure by B:

The closing can also be obtained by

, where X^c denotes the complement

Complement (set theory)

In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...

of X relative to E (that is,

). The above means that the closing is the complement of the locus of translations of the symmetric of the structuring element outside the image A.

Properties of the basic operators

Here are some properties of the basic binary morphological operators (dilation, erosion, opening and closing):

They are translation invariant.
They are increasing, that is, if , then , and , etc.
The dilation is commutative.
If the origin of E belongs to the structuring element B, then .
The dilation is associative, i.e., . Moreover, the erosion satisfies .
Erosion and dilation satisfy the duality .
Opening and closing satisfy the duality .
The dilation is distributive over set union
The erosion is distributive over set intersection
The dilation is a pseudo-inverse of the erosion, and vice-versa, in the following sense: if and only if .
Opening and closing are idempotent.
Opening is anti-extensive, i.e., , whereas the closing is extensive, i.e., .

Other operators and tools

Hit-or-miss transform
Hit-or-miss transform
In mathematical morphology, hit-or-miss transform is an operation that detects a given configuration in a binary image, using the morphological erosion operator and a pair of disjoint structuring elements...
Pruning transform
Pruning (morphology)
The pruning algorithm is a technique used in digital image processing based on mathematical morphology. It is used as a complement to the skeleton and thinning algorithms to remove unwanted parasitic components. In this case 'parasitic' components refer to branches of a line which are not key to...
Morphological skeleton
Morphological skeleton
In digital image processing, morphological skeleton is a skeleton representation of a shape or binary image, computed by means of morphological operators.Morphological skeletons are of two kinds:...
Filtering by reconstruction
Ultimate erosions and conditional bisectors
Granulometry
Granulometry (morphology)
In mathematical morphology, granulometry is an approach to compute a size distribution of grains in binary images, using a series of morphological opening operations...
Geodesic distance functions

Grayscale morphology

In grayscale

Grayscale

In photography and computing, a grayscale or greyscale digital image is an image in which the value of each pixel is a single sample, that is, it carries only intensity information...

morphology, images are functions

Function (mathematics)

mapping a Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

or grid E into

, where

is the set of reals,

is an element larger than any real number, and

is an element smaller than any real number.

Grayscale structuring elements are also functions of the same format, called "structuring functions".

Denoting an image by f(x) and the structuring function by b(x), the grayscale dilation of f by b is given by

where "sup" denotes the supremum

Supremum

In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...

.

Similarly, the erosion of f by b is given by

where "inf" denotes the infimum

Infimum

In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...

.

Just like in binary morphology, the opening and closing are given respectively by

, and

Flat structuring functions

It is common to use flat structuring elements in morphological applications. Flat structuring functions are functions b(x) in the form

where

.

In this case, the dilation and erosion are greatly simplified, and given respectively by

, and

In the bounded, discrete case (E is a grid and B is bounded), the supremum

Supremum

and infimum

Infimum

operators can be replaced by the maximum and minimum. Thus, dilation and erosion are particular cases of order statistics filters, with dilation returning the maximum value within a moving window (the symmetric of the structuring function support B), and the erosion returning the minimum value within the moving window B.

In the case of flat structuring element, the morphological operators depend only on the relative ordering of pixel

Pixel

In digital imaging, a pixel, or pel, is a single point in a raster image, or the smallest addressable screen element in a display device; it is the smallest unit of picture that can be represented or controlled....

values, regardless their numerical values, and therefore are especially suited to the processing of binary images and grayscale images whose light transfer function is not known.

Other operators and tools

Morphological Gradient
Morphological Gradient
In mathematical morphology and digital image processing, a morphological gradient is the difference between the dilation and the erosion of a given image. It is an image where each pixel value indicates the contrast intensity in the close neighborhood of that pixel...

s
Top-hat transform
Top-hat transform
In mathematical morphology and digital image processing, top-hat transform is an operation that extracts small elements and details from given images...
Watershed algorithm
Watershed (algorithm)
A grey-level image may be seen as a topographic relief, where the grey level of a pixel is interpreted as its altitude in the relief.A drop of water falling on a topographic relief flows along a path to finally reach a local minimum...

By combining these operators one can obtain algorithms for many image processing tasks, such as feature detection

Feature extraction

In pattern recognition and in image processing, feature extraction is a special form of dimensionality reduction.When the input data to an algorithm is too large to be processed and it is suspected to be notoriously redundant then the input data will be transformed into a reduced representation...

, image segmentation

Segmentation (image processing)

, image sharpening

Unsharp masking

Unsharp masking is an image manipulation technique, often available in digital image processing software.The "unsharp" of the name derives from the fact that the technique uses a blurred, or "unsharp," positive to create a "mask" of the original image...

, image filtering

Filter (signal processing)

In signal processing, a filter is a device or process that removes from a signal some unwanted component or feature. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal...

, and classification.

Mathematical morphology on complete lattices

Complete lattice

s are partially ordered set

Partially ordered set

In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...

s, where every subset has an infimum

Infimum

and a supremum

Supremum

. In particular, it contains a least element and a greatest element

Greatest element

In mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...

(also denoted "universe").

Adjunctions (Dilation and Erosion)

Let

be a complete lattice, with infimum and supremum symbolized by

and

, respectively. Its universe and least element are symbolized by U and

, respectively. Moreover, let

be a collection of elements from L.

A dilation is any operator

that distributes over the supremum, and preserves the least element. I.e.:

An erosion is any operator

that distributes over the infimum, and preserves the universe. I.e.:

Dilations and erosions form Galois connection

Galois connection

In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...

s. That is, for all dilation

there is one and only one erosion

that satisfies

for all

.

Similarly, for all erosion there is one and only one dilation satisfying the above connection.

Furthermore, if two operators satisfy the connection, then

must be a dilation, and

an erosion.

Pairs of erosions and dilations satisfying the above connection are called "adjunctions", and the erosion is said to be the adjoint erosion of the dilation, and vice-versa.

Opening and Closing

For all adjunction

, the morphological opening

and morphological closing

are defined as follows:

, and

The morphological opening and closing are particular cases of algebraic opening (or simply opening) and algebraic closing (or simply closing). Algebraic openings are operators in L that are idempotent, increasing, and anti-extensive. Algebraic closings are operators in L that are idempotent, increasing, and extensive.

Particular cases

Binary morphology is a particular case of lattice morphology, where L is the power set of E (Euclidean space or grid), that is, L is the set of all subsets of E, and

is the set inclusion. In this case, the infimum is set intersection, and the supremum is set union.

Similarly, grayscale morphology is another particular case, where L is the set of functions mapping E into