Structuring element
Encyclopedia
In mathematical morphology
, a structuring element (s.e.) is a shape, used to probe or interact with a given image, with the purpose of drawing conclusions on how this shape fits or misses the shapes in the image. It is typically used in morphological operations, such as dilation
, erosion
, opening
, and closing
, as well as the hit-or-miss transform
.
According to Georges Matheron
, knowledge about an object (e.g., an image) depends on the manner in which we probe (observe) it. In particular, the choice of a certain s.e. for a particular morphological operation influences the information one can obtain. There are two main characteristics that are directly related to s.e.s:
s are subset
s of an Euclidean space
Rd or the integer grid Zd, for some dimension d. Here are some examples of widely used structuring elements (denoted by B):
In the discrete case, a structuring element can also be represented as a set of pixel
s on a grid
, assuming the values 1 (if the pixel belongs to the structuring element) or 0 (otherwise).
When used by a hit-or-miss transform, usually the structuring element is a composite of two disjoint sets (two simple structuring elements), one associated to the foreground, and one associated to the background of the image to be probed. In this case, an alternative representation of the composite structuring element is as a set of pixel
s which are either set (1, associated to the foreground), not set (0, associated to the background) or "don't care
".
Mathematical morphology
Mathematical morphology is a theory and technique for the analysis and processing of geometrical structures, based on set theory, lattice theory, topology, and random functions...
, a structuring element (s.e.) is a shape, used to probe or interact with a given image, with the purpose of drawing conclusions on how this shape fits or misses the shapes in the image. It is typically used in morphological operations, such as dilation
Dilation (morphology)
Dilation is one of the basic operations in mathematical morphology. Originally developed for binary images, it has been expanded first to grayscale images, and then to complete lattices...
, erosion
Erosion (morphology)
For use of "Erosion" in dermatopathology, see Erosion Erosion is one of two fundamental operations in Morphological image processing from which all other morphological operations are based...
, opening
Opening (morphology)
In mathematical morphology, opening is the dilation of the erosion of a set A by a structuring element B:A\circ B = \oplus B, \, where \ominus and \oplus denote erosion and dilation, respectively....
, and closing
Closing (morphology)
In mathematical morphology, the closing of a set A by a structuring element B is the erosion of the dilation of that set,A\bullet B = \ominus B, \, where \oplus and \ominus denote the dilation and erosion, respectively....
, as well as the hit-or-miss transform
Hit-or-miss transform
In mathematical morphology, hit-or-miss transform is an operation that detects a given configuration in a binary image, using the morphological erosion operator and a pair of disjoint structuring elements...
.
According to Georges Matheron
Georges Matheron
Georges François Paul Marie Matheron was a French mathematician and geologist, known as the founder of geostatistics and a co-founder of mathematical morphology. In 1968 he created the Centre de Géostatistique et de Morphologie Mathématique at the Paris School of Mines in Fontainebleau...
, knowledge about an object (e.g., an image) depends on the manner in which we probe (observe) it. In particular, the choice of a certain s.e. for a particular morphological operation influences the information one can obtain. There are two main characteristics that are directly related to s.e.s:
- Shape. For example, the s.e. can be a ``ball" or a line; convex or a ring, etc. By choosing a particular s.e., one sets a way of differentiating some objects (or parts of objects) from others, according to their shape or spatial orientation.
- Size. For example, one s.e. can be a
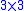square or a 
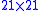square. Setting the size of the structuring element is similar to setting the observation scale, and setting the criterion to differentiate image objects or features according to size.
Mathematical particulars and examples
Structuring elements are particular cases of binary images, usually being small and simple. In mathematical morphology, binary imageBinary image
A binary image is a digital image that has only two possible values for each pixel. Typically the two colors used for a binary image are black and white though any two colors can be used. The color used for the object in the image is the foreground color while the rest of the image is the...
s are subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of an Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rd or the integer grid Zd, for some dimension d. Here are some examples of widely used structuring elements (denoted by B):
- Let E=R2; B is an open disk of radius r, centered at the origin.
- Let E=Z2; B is a 3x3 square, that is, B={(-1,-1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1)}.
- Let E=Z2; B is the "cross" given by: B={(-1,0),(0,-1),(0,0),(0,1),(1,0)}.
In the discrete case, a structuring element can also be represented as a set of pixel
Pixel
In digital imaging, a pixel, or pel, is a single point in a raster image, or the smallest addressable screen element in a display device; it is the smallest unit of picture that can be represented or controlled....
s on a grid
Grid (spatial index)
In the context of a spatial index, a grid is a regular tessellation of a manifold or 2-D surface that divides it into a series of contiguous cells, which can then be assigned unique identifiers and used for spatial indexing purposes...
, assuming the values 1 (if the pixel belongs to the structuring element) or 0 (otherwise).
When used by a hit-or-miss transform, usually the structuring element is a composite of two disjoint sets (two simple structuring elements), one associated to the foreground, and one associated to the background of the image to be probed. In this case, an alternative representation of the composite structuring element is as a set of pixel
Pixel
In digital imaging, a pixel, or pel, is a single point in a raster image, or the smallest addressable screen element in a display device; it is the smallest unit of picture that can be represented or controlled....
s which are either set (1, associated to the foreground), not set (0, associated to the background) or "don't care
Don't Care
"Don't Care" is a 1994 single by American death metal band Obituary. It was released only in the USA, like a previous release of the album World Demise...
".