
Morphological Gradient
Encyclopedia
In mathematical morphology
and digital image processing
, a morphological gradient is the difference between the dilation
and the erosion
of a given image. It is an image where each pixel
value (typically non-negative) indicates the contrast intensity in the close neighborhood of that pixel. It is useful for edge detection
and segmentation
applications.
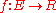 be a grayscale image, mapping points from a Euclidean space or discrete grid E (such as R2 or Z2) into the real line. Let
be a grayscale image, mapping points from a Euclidean space or discrete grid E (such as R2 or Z2) into the real line. Let 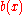 be a grayscale structuring element
be a grayscale structuring element
. Usually, b is symmetric
and has short-support, e.g., .
.
Then, the morphological gradient of f is given by:
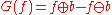 ,
,
where and
and  denote the dilation and the erosion, respectively.
denote the dilation and the erosion, respectively.
An internal gradient is given by:
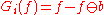 ,
,
and an external gradient is given by:
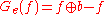 .
.
The internal and external gradients are "thinner" than the gradient, but the gradient peaks are located on the edges, whereas the internal and external ones are located at each side of the edges. Notice that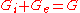 .
.
If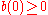 , then all the three gradients have non-negative values at all pixels.
, then all the three gradients have non-negative values at all pixels.
Mathematical morphology
Mathematical morphology is a theory and technique for the analysis and processing of geometrical structures, based on set theory, lattice theory, topology, and random functions...
and digital image processing
Digital image processing
Digital image processing is the use of computer algorithms to perform image processing on digital images. As a subcategory or field of digital signal processing, digital image processing has many advantages over analog image processing...
, a morphological gradient is the difference between the dilation
Dilation (morphology)
Dilation is one of the basic operations in mathematical morphology. Originally developed for binary images, it has been expanded first to grayscale images, and then to complete lattices...
and the erosion
Erosion (morphology)
For use of "Erosion" in dermatopathology, see Erosion Erosion is one of two fundamental operations in Morphological image processing from which all other morphological operations are based...
of a given image. It is an image where each pixel
Pixel
In digital imaging, a pixel, or pel, is a single point in a raster image, or the smallest addressable screen element in a display device; it is the smallest unit of picture that can be represented or controlled....
value (typically non-negative) indicates the contrast intensity in the close neighborhood of that pixel. It is useful for edge detection
Edge detection
Edge detection is a fundamental tool in image processing and computer vision, particularly in the areas of feature detection and feature extraction, which aim at identifying points in a digital image at which the image brightness changes sharply or, more formally, has discontinuities...
and segmentation
Segmentation
Segmentation may mean:*Market segmentation, in economics and marketingBiology*A process of morphogenesis that divides a metazoan body into a series of semi-repetitive segments*Segmentation , a series of semi-repetitive segments...
applications.
Mathematical definition and types
Let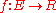 be a grayscale image, mapping points from a Euclidean space or discrete grid E (such as R2 or Z2) into the real line. Let
be a grayscale image, mapping points from a Euclidean space or discrete grid E (such as R2 or Z2) into the real line. Let 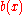 be a grayscale structuring element
be a grayscale structuring elementStructuring element
In mathematical morphology, a structuring element is a shape, used to probe or interact with a given image, with the purpose of drawing conclusions on how this shape fits or misses the shapes in the image...
. Usually, b is symmetric
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
and has short-support, e.g.,
 .
.Then, the morphological gradient of f is given by:
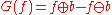 ,
,where
 and
and  denote the dilation and the erosion, respectively.
denote the dilation and the erosion, respectively.An internal gradient is given by:
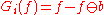 ,
,and an external gradient is given by:
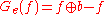 .
.The internal and external gradients are "thinner" than the gradient, but the gradient peaks are located on the edges, whereas the internal and external ones are located at each side of the edges. Notice that
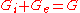 .
.If
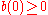 , then all the three gradients have non-negative values at all pixels.
, then all the three gradients have non-negative values at all pixels.External links
- Morphological gradients, Centre de Morphologie Mathématique, École_des_Mines_de_Paris

