
Granulometry (morphology)
Encyclopedia
In mathematical morphology
, granulometry is an approach to compute a size distribution of grains in binary images, using a series of morphological opening
operations. It was introduced by Georges Matheron
in the 1960s, and is the basis for the characterization of the concept of size in mathematical morphology.
in an Euclidean space
or grid
E, and consider the family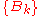 ,
,  , given by:
, given by:
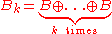 ,
,
where denotes morphological dilation
denotes morphological dilation
. By convention,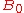 is the set containing only the origin of E, and
is the set containing only the origin of E, and 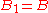 .
.
Let X be a set (i.e., a binary image
in mathematical morphology), and consider the series of sets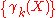 ,
, 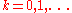 , given by:
, given by:
 ,
,
where denotes the morphological opening.
denotes the morphological opening.
The granulometry function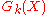 is the cardinality (i.e., area
is the cardinality (i.e., area
or volume
, in continuous Euclidean space, or number of elements, in grids) of the image :
:
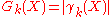 .
.
The pattern spectrum or size distribution of X is the collection of sets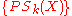 ,
, 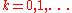 , given by:
, given by:
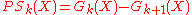 .
.
The parameter k is referred to as size, and the component k of the pattern spectrum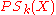 provides a rough estimate for the amount of grains of size k in the image X. Peaks of
provides a rough estimate for the amount of grains of size k in the image X. Peaks of 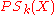 indicate relatively large quantities of grains of the corresponding sizes.
indicate relatively large quantities of grains of the corresponding sizes.
The French
mathematician was inspired by sieving as a means of characterizing size. In sieving, a granular sample is worked through a series of sieve
s with decreasing hole sizes. As a consequence, the different grain
s in the sample are separated according to their sizes.
The operation of passing a sample through a sieve of certain hole size "k" can be mathematically described as an operator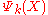 that returns the subset of elements in X with sizes that are smaller or equal to k. This family of operators satisfy the following properties:
that returns the subset of elements in X with sizes that are smaller or equal to k. This family of operators satisfy the following properties:
A granulometry-generating family of operators should satisfy the above three axioms.
In the above case (granulometry generated by a structuring element), .
.
Another example of granulometry-generating family is when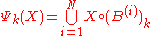 , where
, where  is a set of linear structuring elements with different directions.
is a set of linear structuring elements with different directions.
Mathematical morphology
Mathematical morphology is a theory and technique for the analysis and processing of geometrical structures, based on set theory, lattice theory, topology, and random functions...
, granulometry is an approach to compute a size distribution of grains in binary images, using a series of morphological opening
Opening (morphology)
In mathematical morphology, opening is the dilation of the erosion of a set A by a structuring element B:A\circ B = \oplus B, \, where \ominus and \oplus denote erosion and dilation, respectively....
operations. It was introduced by Georges Matheron
Georges Matheron
Georges François Paul Marie Matheron was a French mathematician and geologist, known as the founder of geostatistics and a co-founder of mathematical morphology. In 1968 he created the Centre de Géostatistique et de Morphologie Mathématique at the Paris School of Mines in Fontainebleau...
in the 1960s, and is the basis for the characterization of the concept of size in mathematical morphology.
Granulometry generated by a structuring element
Let B be a structuring elementStructuring element
In mathematical morphology, a structuring element is a shape, used to probe or interact with a given image, with the purpose of drawing conclusions on how this shape fits or misses the shapes in the image...
in an Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
or grid
Lattice graph
The terms lattice graph, mesh graph, or grid graph refer to a number of categories of graphs whose drawing corresponds to some grid/mesh/lattice, i.e., its vertices correspond to the nodes of the mesh and its edges correspond to the ties between the nodes.-Square grid graph:A common type of a...
E, and consider the family
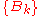 ,
,  , given by:
, given by: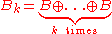 ,
,where
 denotes morphological dilation
denotes morphological dilationDilation (morphology)
Dilation is one of the basic operations in mathematical morphology. Originally developed for binary images, it has been expanded first to grayscale images, and then to complete lattices...
. By convention,
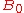 is the set containing only the origin of E, and
is the set containing only the origin of E, and 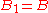 .
.Let X be a set (i.e., a binary image
Binary image
A binary image is a digital image that has only two possible values for each pixel. Typically the two colors used for a binary image are black and white though any two colors can be used. The color used for the object in the image is the foreground color while the rest of the image is the...
in mathematical morphology), and consider the series of sets
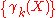 ,
, 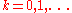 , given by:
, given by: ,
,where
 denotes the morphological opening.
denotes the morphological opening.The granulometry function
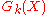 is the cardinality (i.e., area
is the cardinality (i.e., areaArea
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
or volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
, in continuous Euclidean space, or number of elements, in grids) of the image
 :
: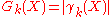 .
.The pattern spectrum or size distribution of X is the collection of sets
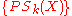 ,
, 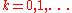 , given by:
, given by: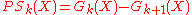 .
.The parameter k is referred to as size, and the component k of the pattern spectrum
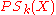 provides a rough estimate for the amount of grains of size k in the image X. Peaks of
provides a rough estimate for the amount of grains of size k in the image X. Peaks of 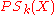 indicate relatively large quantities of grains of the corresponding sizes.
indicate relatively large quantities of grains of the corresponding sizes.Sieving axioms
The above common method is a particular case of the more general approach derived by Matheron.The French
France
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
mathematician was inspired by sieving as a means of characterizing size. In sieving, a granular sample is worked through a series of sieve
Sieve
A sieve, or sifter, separates wanted elements from unwanted material using a woven screen such as a mesh or net. However, in cooking, especially with flour, a sifter is used to aerate the substance, among other things. A strainer is a type of sieve typically used to separate a solid from a liquid...
s with decreasing hole sizes. As a consequence, the different grain
GRAIN
GRAIN is a small international non-profit organisation that works to support small farmers and social movements in their struggles for community-controlled and biodiversity-based food systems. Our support takes the form of independent research and analysis, networking at local, regional and...
s in the sample are separated according to their sizes.
The operation of passing a sample through a sieve of certain hole size "k" can be mathematically described as an operator
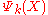 that returns the subset of elements in X with sizes that are smaller or equal to k. This family of operators satisfy the following properties:
that returns the subset of elements in X with sizes that are smaller or equal to k. This family of operators satisfy the following properties:- Anti-extensivity: Each sieve reduces the amount of grains, i.e.,
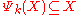 ,
, - Increasingness: The result of sieving a subset of a sample is a subset of the sieving of that sample, i.e.,
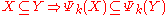 ,
, - "Stability": The result of passing through two sieves is determined by the sieve with smallest hole size. I.e.,
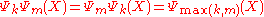 .
.
A granulometry-generating family of operators should satisfy the above three axioms.
In the above case (granulometry generated by a structuring element),
 .
.Another example of granulometry-generating family is when
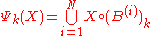 , where
, where  is a set of linear structuring elements with different directions.
is a set of linear structuring elements with different directions.

