Diode modelling
Encyclopedia
In electronics
, diode modelling refers to the mathematical models used to approximate the actual behavior of real diodes to enable calculations and circuit analysis. A diode
's I-V
curve is nonlinear (it is well described by the Shockley diode law). This nonlinearity complicates calculations in circuits involving diodes, so simpler models are often required.
This article discusses the modelling of p-n junction
diodes, but the techniques may be generalized to other solid state
diodes.
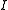of a p-n junction
diode to the diode voltage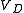
. This relationship is the diode I-V characteristic:
where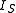
is the saturation current or scale current of the diode (the magnitude of the current that flows for negative 
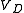in excess of a few 
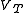, typically 10−12 A). The scale current is proportional to the diode area. Continuing with the symbols: 
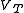is the thermal voltage (
, about 26 mV at normal temperatures), and 
is known as the diode ideality factor (for silicon diodes 
is approximately 1 to 2).
When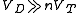
the formula can be simplified to:
This expression is, however, only an approximation of a more complex I-V characteristic. Its applicability is particularly limited in case of ultrashallow junctions, for which better analytical models exist.
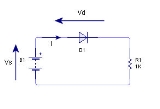
Because the current flowing through the diode is the same as the current throughout the entire circuit, we can lay down another equation. By Kirchhoff's laws
, which boil down to simply Ohm's law
in this case, the current flowing in the circuit is
These two equations determine the diode current and the diode voltage. To solve these two equations, we could substitute the current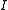
from the second equation into the first equation, and then try to rearrange the resulting equation to get 
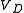in terms of 
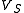. A difficulty with this method is that the diode law is nonlinear. Nonetheless, a formula expressing 
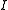directly in terms of 
without involving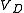 
can be obtained using the Lambert 
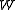-function, which is the inverse function
of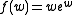
, that is, 
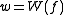. This solution is discussed next.
An explicit expression for the diode current can be obtained in terms of the Lambert W-function (also called the Omega function). A guide to these manipulations follows. A new variable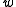
is introduced as
Following the substitutions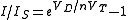
and 
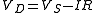, rearrangement of the diode law in terms of w becomes
which using the Lambert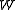
-function becomes
With the approximations (valid for the most common values of the parameters)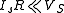
and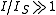 
, this solution becomes
Once the current is determined, the diode voltage can be found using either of the other equations.
The diode voltage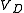
can be found in terms of 
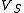for any particular set of values by an iterative method
using a calculator or computer The diode law is rearranged by dividing by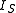
, and adding 1. The diode law becomes
By taking natural logarithms of both sides the exponential is removed, and the equation becomes
For any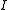
, this equation determines 
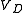. However, 
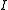also must satisfy the Kirchhoff's law equation, given above. This expression is substituted for 
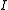to obtain
or
The voltage of the source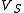
is a known given value, but 
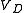is on both sides of the equation, which forces an iterative solution: a starting value for 
is guessed and put into the right side of the equation. Carrying out the various operations on the right side, we come up with a new value for 
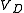. This new value now is substituted on the right side, and so forth. If this iteration converges the values of 
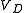become closer and closer together as the process continues, and we can stop iteration when the accuracy is sufficient. Once 
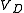is found, 
can be found from the Kirchhoff's law equation.
Sometimes an iterative procedure depends critically on the first guess. In this example, almost any first guess will do, say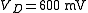
. Sometimes an iterative procedure does not converge at all: in this problem an iteration based on the exponential function does not converge, and that is why the equations were rearranged to use a logarithm. Finding a convergent iterative formulation is an art, and every problem is different.
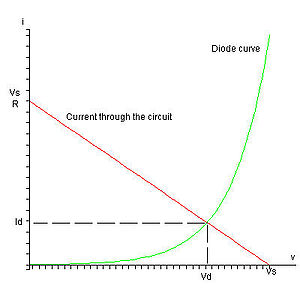
Graphical analysis is a simple way to derive a numerical solution to the transcendental
equations describing the diode. As with most graphical methods, it has the advantage of easy visualization. By plotting the I-V curves, it is possible to obtain an approximate solution to any arbitrary degree of accuracy. This process is the graphical equivalent of the two previous approaches, which are more amenable to computer implementation.
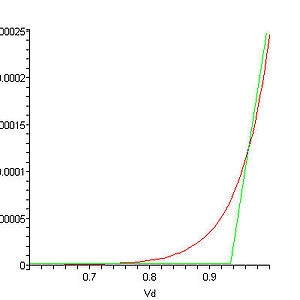
This method plots the two current-voltage equations on a graph and the point of intersection of the two curves satisfies both equations, giving the value of the current flowing through the circuit and the voltage across the diode. The following figure illustrates such method.
. The figure below shows a real diode I-V curve being approximated by a two-segment piecewise linear model. Typically the sloped line segment would be chosen tangent to the diode curve at the Q-point. Then the slope of this line is given by the reciprocal of the small-signal resistance of the diode at the Q-point.
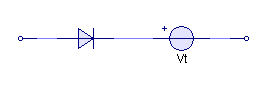When forward biased, the ideal diode is simply a short circuit and when reverse biased, an open circuit.
If the anode
of the diode is connected to 0 V, the voltage at the cathode
will be at Vt and so the potential at the cathode will be greater than the potential at the anode and the diode will be reverse biased. In order to get the diode to conduct, the voltage at the anode will need to be taken to Vt. This circuit approximates the cut-in voltage present in real diodes. The combined I-V characteristic of this circuit is shown below:
The Shockley diode model can be used to predict the approximate value of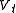 
.
Electronics
Electronics is the branch of science, engineering and technology that deals with electrical circuits involving active electrical components such as vacuum tubes, transistors, diodes and integrated circuits, and associated passive interconnection technologies...
, diode modelling refers to the mathematical models used to approximate the actual behavior of real diodes to enable calculations and circuit analysis. A diode
Diode
In electronics, a diode is a type of two-terminal electronic component with a nonlinear current–voltage characteristic. A semiconductor diode, the most common type today, is a crystalline piece of semiconductor material connected to two electrical terminals...
's I-V
Voltage
Voltage, otherwise known as electrical potential difference or electric tension is the difference in electric potential between two points — or the difference in electric potential energy per unit charge between two points...
curve is nonlinear (it is well described by the Shockley diode law). This nonlinearity complicates calculations in circuits involving diodes, so simpler models are often required.
This article discusses the modelling of p-n junction
P-n junction
A p–n junction is formed at the boundary between a P-type and N-type semiconductor created in a single crystal of semiconductor by doping, for example by ion implantation, diffusion of dopants, or by epitaxy .If two separate pieces of material were used, this would...
diodes, but the techniques may be generalized to other solid state
Solid state (electronics)
Solid-state electronics are those circuits or devices built entirely from solid materials and in which the electrons, or other charge carriers, are confined entirely within the solid material...
diodes.
Shockley diode model
The Shockley diode equation relates the diode current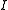 of a p-n junctionP-n junction
A p–n junction is formed at the boundary between a P-type and N-type semiconductor created in a single crystal of semiconductor by doping, for example by ion implantation, diffusion of dopants, or by epitaxy .If two separate pieces of material were used, this would...
diode to the diode voltage
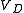. This relationship is the diode I-V characteristic:-
,
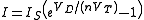where
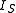is the saturation current or scale current of the diode (the magnitude of the current that flows for negative 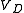in excess of a few 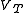, typically 10−12 A). The scale current is proportional to the diode area. Continuing with the symbols: 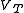is the thermal voltage (, about 26 mV at normal temperatures), and is known as the diode ideality factor (for silicon diodes is approximately 1 to 2).When
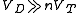the formula can be simplified to:-
.
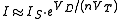This expression is, however, only an approximation of a more complex I-V characteristic. Its applicability is particularly limited in case of ultrashallow junctions, for which better analytical models exist.
Diode-resistor circuit example
To illustrate the complications in using this law, consider the problem of finding the voltage across the diode in Figure 1.Because the current flowing through the diode is the same as the current throughout the entire circuit, we can lay down another equation. By Kirchhoff's laws
Kirchhoff's circuit laws
Kirchhoff's circuit laws are two equalities that deal with the conservation of charge and energy in electrical circuits, and were first described in 1845 by Gustav Kirchhoff...
, which boil down to simply Ohm's law
Ohm's law
Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points...
in this case, the current flowing in the circuit is
-
.
These two equations determine the diode current and the diode voltage. To solve these two equations, we could substitute the current
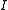from the second equation into the first equation, and then try to rearrange the resulting equation to get 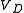in terms of 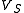. A difficulty with this method is that the diode law is nonlinear. Nonetheless, a formula expressing 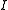directly in terms of without involving 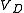can be obtained using the Lambert 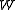-function, which is the inverse functionInverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of
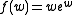, that is, 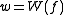. This solution is discussed next.Explicit solution
An explicit expression for the diode current can be obtained in terms of the Lambert W-function (also called the Omega function). A guide to these manipulations follows. A new variable
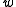is introduced as-
.
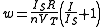Following the substitutions
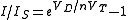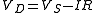and , rearrangement of the diode law in terms of w becomes-
,
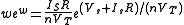which using the Lambert
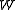-function becomes-
.
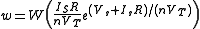With the approximations (valid for the most common values of the parameters)
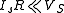and 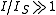, this solution becomes-
.
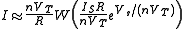Once the current is determined, the diode voltage can be found using either of the other equations.
Iterative solution
The diode voltage
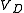can be found in terms of 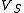for any particular set of values by an iterative methodIterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
using a calculator or computer The diode law is rearranged by dividing by
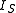, and adding 1. The diode law becomes-
.
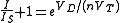By taking natural logarithms of both sides the exponential is removed, and the equation becomes
-
.
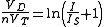For any
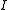, this equation determines 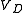. However, 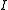also must satisfy the Kirchhoff's law equation, given above. This expression is substituted for 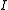to obtain-
,
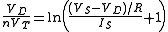or
-
.
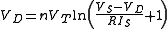The voltage of the source
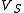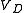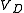is a known given value, but is on both sides of the equation, which forces an iterative solution: a starting value for is guessed and put into the right side of the equation. Carrying out the various operations on the right side, we come up with a new value for . This new value now is substituted on the right side, and so forth. If this iteration converges the values of 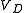become closer and closer together as the process continues, and we can stop iteration when the accuracy is sufficient. Once 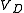is found, can be found from the Kirchhoff's law equation.Sometimes an iterative procedure depends critically on the first guess. In this example, almost any first guess will do, say
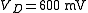. Sometimes an iterative procedure does not converge at all: in this problem an iteration based on the exponential function does not converge, and that is why the equations were rearranged to use a logarithm. Finding a convergent iterative formulation is an art, and every problem is different.Graphical solution
Graphical analysis is a simple way to derive a numerical solution to the transcendental
Transcendental function
A transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...
equations describing the diode. As with most graphical methods, it has the advantage of easy visualization. By plotting the I-V curves, it is possible to obtain an approximate solution to any arbitrary degree of accuracy. This process is the graphical equivalent of the two previous approaches, which are more amenable to computer implementation.
This method plots the two current-voltage equations on a graph and the point of intersection of the two curves satisfies both equations, giving the value of the current flowing through the circuit and the voltage across the diode. The following figure illustrates such method.
Piecewise linear model
In practice, the graphical method is complicated and impractical for complex circuits. Another method of modelling a diode is called piecewise linear (PWL) modelling. In mathematics, this means taking a function and breaking it down into several linear segments. This method is used to approximate the diode characteristic curve as a series of linear segments. The real diode is modeled as 3 components in series: an ideal diode, a voltage source and a resistorResistor
A linear resistor is a linear, passive two-terminal electrical component that implements electrical resistance as a circuit element.The current through a resistor is in direct proportion to the voltage across the resistor's terminals. Thus, the ratio of the voltage applied across a resistor's...
. The figure below shows a real diode I-V curve being approximated by a two-segment piecewise linear model. Typically the sloped line segment would be chosen tangent to the diode curve at the Q-point. Then the slope of this line is given by the reciprocal of the small-signal resistance of the diode at the Q-point.
Mathematically idealized diode
Firstly, let us consider a mathematically idealized diode. In such an ideal diode, if the diode is reverse biased, the current flowing through it is zero. This ideal diode starts conducting at 0 V and for any positive voltage an infinite current flows and the diode acts like a short circuit. The I-V characteristics of an ideal diode are shown below:Ideal diode in series with voltage source
Now let us consider the case when we add a voltage source in series with the diode in the form shown below:If the anode
Anode
An anode is an electrode through which electric current flows into a polarized electrical device. Mnemonic: ACID ....
of the diode is connected to 0 V, the voltage at the cathode
Cathode
A cathode is an electrode through which electric current flows out of a polarized electrical device. Mnemonic: CCD .Cathode polarity is not always negative...
will be at Vt and so the potential at the cathode will be greater than the potential at the anode and the diode will be reverse biased. In order to get the diode to conduct, the voltage at the anode will need to be taken to Vt. This circuit approximates the cut-in voltage present in real diodes. The combined I-V characteristic of this circuit is shown below:
.-
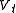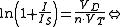
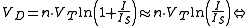
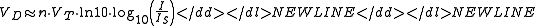
Using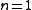
and 
:
Typical values of the saturation currentSaturation currentSaturation current is a term used in relation to semiconductor diodes. It is more fully, and accurately, named reverse saturation current and is "part of the reverse current in a diode caused by diffusion of minority carriers from the neutral regions to the depletion region...
are: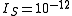
for silicon diodes;
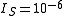for germanium diodes.
As the variation of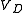
goes with the logarithm of the ratio 
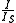, its value varies very little for a big variation of the ratio. The use of base 10 logarithms makes it easier to
think in orders of magnitude.
For a current of 1.0 mA: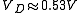
for silicon diodes (9 orders of magnitude);
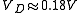for germanium diodes (3 orders of magnitude).
For a current of 100 mA: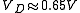
for silicon diodes (11 orders of magnitude);
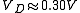for germanium diodes (5 orders of magnitude).
Values of 0.6 or 0.7 Volts are commonly used for silicon diodes
Diode with voltage source and current-limiting resistor
The last thing needed is a resistor to limit the current, as shown below:
The I-V characteristic of the final circuit looks like this: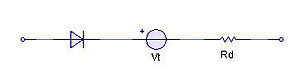
The real diode now can be replaced with the combined ideal diode, voltage source and resistor and the circuit then is modelled using just linear elements. If the sloped-line segment is tangent to the real diode curve at the Q-point, this approximate circuit has the same small-signal circuit at the Q-point as the real diode.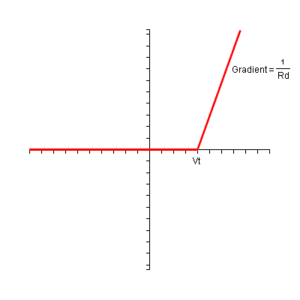
Dual PWL-diodes or 3-Line PWL model
When more accuracy is desired in modeling the diode's turn-on characteristic, the model can be enhanced by doubling-up the standard PWL-model. This model uses two piecewise-linear diodes in parallel, as a way to model a single diode more accurately.
Resistance
Using the Shockley equation, the small-signal diode resistance
of the diode can be derived about some operating point (Q-point) where the DC bias current is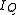 
and the Q-point applied voltage is 
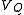. To begin, the diode small-signal conductance 
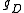is found, that is, the change in current in the diode caused by a small change in voltage across the diode, divided by this voltage change, namely:
-
.
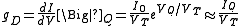The latter approximation assumes that the bias current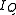
is large enough so that the factor of 1 in the parentheses of the Shockley diode equation can be ignored. This approximation is accurate even at rather small voltages, because the thermal voltage 
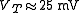at 300K, so 
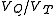tends to be large, meaning that the exponential is very large.
Noting that the small-signal resistance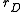
is the reciprocal of the small-signal conductance just found, the diode resistance is independent of the ac current, but depends on the dc current, and is given as
-
.
Capacitance
The charge in the diode carrying current
is known to be
,
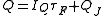where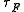
is the forward transit time of charge carriers: The first term in the charge is the charge in transit across the diode when the current 
flows. The second term is the charge stored in the junction itself when it is viewed as a simple capacitorCapacitanceIn electromagnetism and electronics, capacitance is the ability of a capacitor to store energy in an electric field. Capacitance is also a measure of the amount of electric potential energy stored for a given electric potential. A common form of energy storage device is a parallel-plate capacitor...
; that is, as a pair of electrodes with opposite charges on them. It is the charge stored on the diode by virtue of simply having a voltage across it, regardless of any current it conducts.
In a similar fashion as before, the diode capacitance is the change in diode charge with diode voltage:
-
,
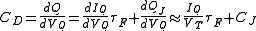where
is the junction capacitance and the first term is called the diffusion capacitanceDiffusion capacitanceDiffusion capacitance is the capacitance due to transport of charge carriers between two terminals of a device, for example, the diffusion of carriers from anode to cathode in forward bias mode of a diode or from emitter to base for a transistor...
, because it is related to the current diffusing through the junction.-
