
Divergent geometric series
Encyclopedia
In mathematics
, an infinite geometric series of the form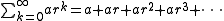
is divergent
if and only if | r | ≥ 1. Methods for summation of divergent series
are sometimes useful, and usually evaluate divergent geometric series to a sum that agrees with the formula for the convergent case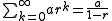 .
.
This is true of any summation method that possesses the properties of regularity, linearity, and stability
.
, given certain restrictions on S, then the method also gives the analytic continuation
of any other function on the intersection of S with the Mittag-Leffler star
for f.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an infinite geometric series of the form
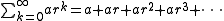
is divergent
Divergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
if and only if | r | ≥ 1. Methods for summation of divergent series
Divergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
are sometimes useful, and usually evaluate divergent geometric series to a sum that agrees with the formula for the convergent case
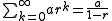 .
.This is true of any summation method that possesses the properties of regularity, linearity, and stability
Stability
-Mathematics:*Stability theory, the study of the stability of solutions to differential equations and dynamical systems**Lyapunov stability**Structural stability*Stability of a point in geometric invariant theory....
.
Examples
In increasing order of difficulty to sum:- 1 − 1 + 1 − 1 + · · ·, whose common ratio is −1
- 1 − 2 + 4 − 8 + · · ·, whose common ratio is −2
- 1 + 2 + 4 + 8 + · · ·1 + 2 + 4 + 8 + · · ·In mathematics, 1 + 2 + 4 + 8 + … is the infinite series whose terms are the successive powers of two. As a geometric series, it is characterized by its first term, 1, and its common ratio, 2. As a series of real numbers it diverges to infinity, so in the usual sense it has no sum...
, whose common ratio is 2 - 1 + 1 + 1 + 1 + · · ·, whose common ratio is 1.
Motivation for study
It is useful to figure out which summation methods produce the geometric series formula for which common ratios. One application for this information is the so-called Borel-Okada principle: If a regular summation method sums Σzn to 1/(1 - z) for all z in a subset S of the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, given certain restrictions on S, then the method also gives the analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
of any other function on the intersection of S with the Mittag-Leffler star
Mittag-Leffler star
In complex analysis, a branch of mathematics, the Mittag-Leffler star of a complex-analytic function is a set in the complex plane obtained by attempting to extend that function along rays emanating from a given point...
for f.

