Divisibility rule
Encyclopedia
A divisibility rule is a shorthand way of discovering whether a given number is divisible by a fixed divisor without performing the division, usually by examining its digits. Although there are divisibility tests for numbers in any radix
, and they are all different, this article presents rules and examples only for decimal
numbers.
For divisors with multiple rules, the rules are generally ordered first for those appropriate for numbers with many digits, then those useful for numbers with fewer digits.
Note: To test divisibility by any number that can be expressed as 2n or 5n, in which n is a positive integer, just examine the last n digits.
Example
If a number is a multiplication of 3 consecutive numbers then that number is always divisible by 3. This is useful for when the number takes the form of (n × (n − 1) × (n + 1))
Ex.
Ex.
Alternatively, one can simply divide the number by 2, and then check the result to find if it is divisible by 2. If it is, the original number is divisible by 4. In addition, the result of this test is the same as the original number divided by 4.
Ex.
General rule
Alternative example
If the last digit in the number is 0, then the result will be the remaining digits multiplied by 2. For example, the number 40 ends in a zero (0), so take the remaining digits (4) and multiply that by two (4 × 2 = 8). The result is the same as the result of 40 divided by 5(40/5 = 8).
If the last digit in the number is 5, then the result will be the remaining digits multiplied by two (2), plus one (1). For example, the number 125 ends in a 5, so take the remaining digits (12), multiply them by two (12 × 2 = 24), then add one (24 + 1 = 25). The result is the same as the result of 125 divided by 5 (125/5=25).
Ex.
If the last digit is 0
If the last digit is 5
Alternatively, one can check for divisibility by six by taking the number (246), dropping the last digit in the number (246, adding together the remaining number (24 becomes 2 + 4 = 6), multiplying that by four (6 × 4 = 24), and adding the last digit of the original number to that (24 + 6 = 30). If this number is divisible by six, the original number is divisible by 6.
If the number is divisible by six, take the original number (246) and divide it by two (246 ÷ 2 = 123). Then, take that result and divide it by three (123 ÷ 3 = 41). This result is the same as the original number divided by six (246 ÷ 6 = 41).
Ex.
General rule
Finding a remainder of a number when divided by 6
6 − (1, −2, −2, −2, −2, and −2 goes on for the rest) No period.
Minimum magnitude sequence
(1, 4, 4, 4, 4, and 4 goes on for the rest)
Positive sequence
Multiply the right most digit by the left most digit in the sequence and multiply the second right most digit by the second left most digit in the sequence and so on. Next, compute the sum of all the values and take the remainder on division by 6.
Example: What is the remainder when 1036125837 is divided by 6?
Multiplication of the rightmost digit = 1 × 7 = 7
Multiplication of the second rightmost digit = 3 × −2 = −6
Third rightmost digit = −16
Fourth rightmost digit = −10
Fifth rightmost digit = −4
Sixth rightmost digit = −2
Seventh rightmost digit = −12
Eighth rightmost digit = −6
Ninth rightmost digit = 0
Tenth rightmost digit = −2
Sum = −51
−51 modulo 6 = 3
Remainder = 3
) is obtained. The original number is divisible by 7 if and only if the number obtained using this procedure is divisible by 7. For example, the number 371: 37 − (2×1) = 37 − 2 = 35; 3 − (2 × 5) = 3 − 10 = −7; thus, since −7 is divisible by 7, 371 is divisible by 7.
Another method is multiplication by 3. A number of the form 10x + y has the same remainder when divided by 7 as 3x + y. So get the leftmost digit of the original number, multiply by 3, add the next digit, get the remainder by 7, and continue from the beginning: multiply by 3, add the next digit, etc. For example, the number 371: 3×3 + 7 = 16 remainder 2, and 2×3 + 1 = 7. This method can be used to find the remainder of division by 7.
A more complicated algorithm for testing divisibility by 7 uses the fact that 100 ≡ 1, 101 ≡ 3, 102 ≡ 2, 103 ≡ 6, 104 ≡ 4, 105 ≡ 5, 106 ≡ 1, ... (mod 7). Take each digit of the number (371) in reverse order (173), multiplying them successively by the digits 1, 3, 2, 6, 4, 5, repeating with this sequence of multipliers as long as necessary (1, 3, 2, 6, 4, 5, 1, 3, 2, 6, 4, 5, ...), and adding the products (1×1 + 7×3 + 3×2 = 1 + 21 + 6 = 28). The original number is divisible by 7 if and only if the number obtained using this procedure is divisible by 7 (hence 371 is divisible by 7 since 28 is).
This method can be simplified by removing the need to multiply. All it would take with this simplification is to memorise the sequence above (132645...), and to add and subtract, but always working with one-digit numbers.
The simplification goes as follows:
If through this procedure you obtain a 0 or any recognisable multiple of 7, then the original number is a multiple of 7. If you obtain any number from 1 to 6, that will indicate how much you should subtract from the original number to get a multiple of 7. In other words, you will find the remainder
of dividing the number by 7. For example take the number 186:
Now, change 1 into the following digit in the sequence (3), add it to the second digit, and write the result instead of both: 3 + 1 = 4. So 116 becomes now 46 .
Repeat the procedure, since the number is greater than 7. Now, 4 becomes 5, which must be added to 6. That is 11.
Repeat the procedure one more time: 1 becomes 3, which is added to the second digit (1): 3 + 1 = 4.
Now we have a number lower than 7, and this number (4) is the remainder of dividing 186/7. So 186 minus 4, which is 182, must be a multiple of 7.
Note: The reason why this works is that if we have: a+b=c and b is a multiple of any given number n, then a and c will necessarily produce the same remainder when divided by n. In other words, in 2 + 7 = 9, 7 is divisible by 7. So 2 and 9 must have the same reminder when divided by 7. The remainder is 2.
Therefore, if a number n is a multiple of 7 (i.e.: the remainder of n/7 is 0), then adding (or subtracting) multiples of 7 cannot possibly change that property.
What this procedure does, as explained above for most divisibility rules, is simply subtract little by little multiples of 7 from the original number until reaching a number that is small enough for us to remember if it is a multiple of 7 or not. If 1 becomes a 3 in the following decimal position, that is just the same as converting 10×10n into a 3×10n. And that is actually the same as subtracting 7×10n (clearly a multiple of 7) from 10×10n.
Similarly, when you turn a 3 into a 2 in the following decimal position, you are turning 30×10n into 2×10n, which is the same as subtracting 30×10n−28×10n, and this is again subtracting a multiple of 7. The same reason applies for all the remaining conversions:
First method example
1050 → 105 − 0=105 → 10 − 10 = 0. ANSWER: 1050 is divisible by 7.
Second method example
1050 → 0501 (reverse) → 0×1 + 5×3 + 0×2 + 1×6 = 0 + 15 + 0 + 6 = 21 (multiply and add). ANSWER: 1050 is divisible by 7.
Vedic method of divisibility by osculation
Divisibility by seven can be tested by multiplication by the Ekhādika. Convert the divisor seven to the nines family by multiplying by seven. 7×7=49. Add one, drop the units digit and, take the 5, the Ekhādika, as the multiplier. Start on the right. Multiply by 5, add the product to the next digit to the left. Set down that result on a line below that digit. Repeat that method of multiplying the units digit by five and adding that product to the number of tens. Add the result to the next digit to the left. Write down that result below the digit. Continue to the end. If the end result is zero or a multiple of seven, then yes, the number is divisible by seven. Otherwise, it is not. This follows the Vedic ideal, one-line notation.
Vedic method example:
Is 438,722,025 divisible by seven? Multiplier = 5.
4 3 8 7 2 2 0 2 5
42 37 46 37 6 40 37 27
YES
Pohlman–Mass method of divisibility by 7
The Pohlman–Mass method provides a quick solution that can determine if most integers are divisible by seven in three steps or less. This method could be useful in a mathematics competition such as MATHCOUNTS, where time is a factor to determine the solution without a calculator in the Sprint Round.
Step A:
If the integer is 1,000 or less, subtract twice the last digit from the number formed by the remaining digits. If the result is a multiple of seven, then so is the original number (and vice versa). For example:
112 -> 11 − (2×2) = 11 − 4 = 7 YES
98 -> 9 − (8×2) = 9 − 16 = −7 YES
634 -> 63 − (4×2) = 63 − 8 = 55 NO
Because 1,001 is divisible by seven, an interesting pattern develops for repeating sets of 1, 2, or 3 digits that form 6-digit numbers (leading zeros are allowed) in that all such numbers are divisible by seven. For example:
001 001 = 1,001 / 7 = 143
010 010 = 10,010 / 7 = 1,430
011 011 = 11,011 / 7 = 1,573
100 100 = 100,100 / 7 = 14,300
101 101 = 101,101 / 7 = 14,443
110 110 = 110,110 / 7 = 15,730
01 01 01 = 10,101 / 7 = 1,443
10 10 10 = 101,010 / 7 = 14,430
111,111 / 7 = 15,873
222,222 / 7 = 31,746
999,999 / 7 = 142,857
576,576 / 7 = 82,368
For all of the above examples, subtracting the first thee digits from the last three results in a multiple of seven. Notice that leading zeros are permitted to form a 6-digit pattern.
This phenomenon forms the basis for Steps B and C.
Step B:
If the integer is between 1,001 and one million, find a repeating pattern of 1, 2, or 3 digits that forms a 6-digit number that is close to the integer (leading zeros are allowed and can help you visualize the pattern). If the positive difference is less than 1,000, apply Step A. This can be done by subtracting the first three digits from the last three digits. For example:
341,355 − 341,341 = 14 -> 1 − (4×2) = 1 − 8 = −7 YES
67,326 − 067,067 = 259 -> 25 − (9×2) = 25 − 18 = 7 YES
The fact that 999,999 is a multiple of 7 can be used for determining divisibility of integers larger than one million by reducing the integer to a 6-digit number that can be determined using Step B. This can be done easily by adding the digits left of the first six to the last six and follow with Step A.
Step C:
If the integer is larger than one million, subtract the nearest multiple of 999,999 and then apply Step B. For even larger numbers, use larger sets such as 12-digits (999,999,999,999) and so on. Then, break the integer into a smaller number that can be solved using Step B. For example:
22,862,420 − (999,999 × 22) = 22,862,420 − 21,999,978 -> 862,420 + 22 = 862,442
862,442 -> 862 − 442 (Step B) = 420 -> 42 − (0×2) (Step A) = 42 YES
This allows adding and subtracting alternating sets of three digits to determine divisibility by seven. Understanding these patterns allows you to quickly calculate divisibility of seven as seen in the following examples:
Pohlman–Mass method of divisibility by 7, examples:
Is 98 divisible by seven?
98 -> 9 − (8×2) = 9 − 16 = −7 YES (Step A)
Is 634 divisible by seven?
634 -> 63 − (4×2) = 63 − 8 = 55 NO (Step A)
Is 355,341 divisible by seven?
355,341 − 341,341 = 14,000 (Step B) -> 014 − 000 (Step B) -> 14 = 1 − (4×2) (Step A) = 1 − 8 = −7 YES
Is 42,341,530 divisible by seven?
42,341,530 -> 341,530 + 42 = 341,572 (Step C)
341,572 − 341,341 = 231 (Step B)
231 -> 23 − (1×2) = 23 − 2 = 21 YES (Step A)
Using quick alternating additions and subtractions:
42,341,530 -> 530 − 341 = 189 + 42 = 231 -> 23 − (1×2) = 21 YES
Multiplication by 3 method of divisibility by 7, examples:
Is 98 divisible by seven?
98 -> 9 remainder 2 -> 2×3 + 8 = 14 YES
Is 634 divisible by seven?
634 -> 6×3 + 3 = 21 -> remainder 0 -> 0×3 + 4 = 4 NO
Is 355,341 divisible by seven?
3 * 3 + 5 = 14 -> remainder 0 -> 0×3 + 5 = 5 -> 5×3 + 3 = 18 -> remainder 4 -> 4×3 + 4 = 16 -> remainder 2 -> 2×3 + 1 = 7 YES
Find remainder of 1036125837 divided by 7
1×3 + 0 = 3
3×3 + 3 = 12 remainder 5
5×3 + 6 = 21 remainder 0
0×3 + 1 = 1
1×3 + 2 = 5
5×3 + 5 = 20 remainder 6
6×3 + 8 = 26 remainder 5
5×3 + 3 = 18 remainder 4
4×3 + 7 = 19 remainder 5
Answer is 5
Finding remainder of a number when divided by 7
7 − (1, 3, 2, −1, −3, −2, cycle repeats for the next six digits) Period: 6 digits.
Recurring numbers: 1, 3, 2, −1, −3, −2
Minimum magnitude sequence
(1, 3, 2, 6, 4, 5, cycle repeats for the next six digits) Period: 6 digits.
Recurring numbers: 1, 3, 2, 6, 4, 5
Positive sequence
Multiply the right most digit by the left most digit in the sequence and multiply the second right most digit by the second left most digit in the sequence and so on and so for. Next, compute the sum of all the values and take the modulus of 7.
Example: What is the remainder when 1036125837 is divided by 7?
Multiplication of the rightmost digit = 1 × 7 = 7
Multiplication of the second rightmost digit = 3 × 3 = 9
Third rightmost digit = 8 × 2 = 16
Fourth rightmost digit = 5 × −1 = −5
Fifth rightmost digit = 2 × −3 = −6
Sixth rightmost digit = 1 × −2 = −2
Seventh rightmost digit = 6 × 1 = 6
Eighth rightmost digit = 3 × 3 = 9
Ninth rightmost digit = 0
Tenth rightmost digit = 1 × −1 = −1
Sum = 33
33 modulus 7 = 5
Remainder = 5
Digit pair method of divisibility by 7
This method uses 1, −3, 2 pattern on the digit pairs. That is, the divisibility of any number by seven can be tested by first separating the number into digit pairs, and then applying the algorithm on three digit pairs (six digits). When the number is smaller than six digits, then fill zero’s to the right side until there are six digits. When the number is larger than six digits, then repeat the cycle on the next six digit group and then add the results. Repeat the algorithm until the result is a small number. The original number is divisible by seven if and only if the number obtained using this algorithm is divisible by seven. This method is especially suitable for large numbers.
Example 1:
The number to be tested is 157514.
First we separate the number into three digit pairs: 15, 75 and 14.
Then we apply the algorithm: 1 × 15 − 3 × 75 + 2 × 14 = 182
Because the resulting 182 is less than six digits, we add zero’s to the right side until it is six digits.
Then we apply our algorithm again: 1 × 18 − 3 × 20 + 2 × 0 = −42
The result −42 is divisible by seven, thus the original number 157514 is divisible by seven!
Example 2:
The number to be tested is 15751537186.
(1 × 15 − 3 × 75 + 2 × 15) + (1 × 37 − 3 × 18 + 2 × 60) = −180 + 103 = −77
The result −77 is divisible by seven, thus the original number 15751537186 is divisible by seven!
13 (1, −3, −4, −1, 3, 4, cycle goes on.)
If you are not comfortable with negative numbers, then use this sequence. (1, 10, 9, 12, 3, 4)
Multiply the right most digit of the number with the left most number in the sequence shown above and the second right most digit to the second left most digit of the number in the sequence. The cycle goes on.
Example: What is the remainder when 321 is divided by 13?
Using the first sequence,
Ans: 1 × 1 + 2 × −3 + 3 × −4 = 9
Remainder = −17 mod 13 = 9
Example: What is the remainder when 1234567 is divided by 13?
Using the second sequence,
Answer: 7 × 1 + 6 × 10 + 5 × 9 + 4 × 12 + 3 × 3 + 2 × 4 + 1 × 1 = 178 mod 13 = 9
Remainder = 9
factors. For example, to determine divisibility by 24, check divisibility by 8 and by 3. Note that checking 4 and 6, or 2 and 12, would not be sufficient. A table of prime factors
may be useful.
A composite
divisor may also have a rule formed using the same procedure as for a prime divisor, given below, with the caveat that the manipulations involved may not introduce any factor which is present in the divisor. For instance, one can not make a rule for 14 that involves multiplying the equation by 7. This is not an issue for prime divisors because they have no smaller factors.
Using 17 as an example, since 10 × (−5) = −50 = 1 mod 17, we get the rule for using y − 5x in the table above. In fact, this rule for prime divisors besides 2 and 5 is really a rule
for divisibility by any integer relatively prime to 10 (including 21 and 27; see tables below). This is why the last divisibility condition in the tables above and below for any number relatively prime to 10 has the same kind of form (add or subtract some multiple of the last digit from the rest of the number).
s and rearranging them. By writing a number as the sum of each digit times a power of 10
each digit's power can be manipulated individually.
Case where all digits are summed
This method works for divisors that are factors of 10 − 1 = 9.
Using 3 as an example, 3 divides 9 = 10 − 1. That means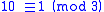
(see modular arithmetic
). The same for all the higher powers of 10:
They are all congruent
to 1 modulo 3. Since two things that are congruent modulo 3 are either both divisible by 3 or both not, we can interchange values that are congruent modulo 3. So, in a number such as the following, we can replace all the powers of 10 by 1:
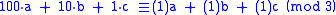
which is exactly the sum of the digits.
Case where the alternating sum of digits is used
This method works for divisors that are factors of 10 + 1 = 11.
Using 11 as an example, 11 divides 11 = 10 + 1. That means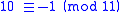
. For the higher powers of 10, they are congruent to 1 for even powers and congruent to −1 for odd powers:
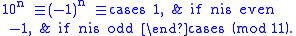
Like the previous case, we can substitute powers of 10 with congruent values:
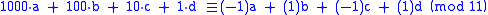
which is also the difference between the sum of digits at odd positions and the sum of digits at even positions.
Case where only the last digit(s) matter
This applies to divisors that are a factor of a power of 10. This is because sufficiently high powers of the base are multiples of the divisor, and can be eliminated.
For example, in base 10, the factors of 101 include 2, 5, and 10. Therefore, divisibility by 2, 5, and 10 only depend on whether the last 1 digit is divisible by those divisors. The factors of 102 include 4 and 25, and divisibility by those only depend on the last 2 digits.
Case where only the last digit(s) are removed
Most numbers do not divide 9 or 10 evenly, but do divide a higher power of 10n or 10n − 1. In this case the number is still written in powers of 10, but not fully expanded.
For example, 7 does not divide 9 or 10, but does divide 98, which is close to 100. Thus, proceed from
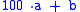
where in this case a is any integer, and b can range from 0 to 99. Next,
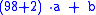
and again expanding
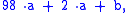
and after eliminating the known multiple of 7, the result is
which is the rule "double the number formed by all but the last two digits, then add the last two digits".
Case where the last digit(s) is multiplied by a factor
The representation of the number may also be multiplied by any number relatively prime to the divisor without changing its divisibility. After observing that 7 divides 21, we can perform the following:
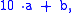
after multiplying by 2, this becomes
and then
Eliminating the 21 gives
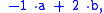
and multiplying by −1 gives
Either of the last two rules may be used, depending on which is easier to perform. They correspond to the rule "subtract twice the last digit from the rest".
; for divisibility other than by 2's and 5's the proofs rest on the basic fact that 10 mod m is invertible if 10 and m are relatively prime.
For 2n or 5n:
Only the last n digits need to be checked.
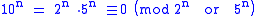
Representing x as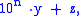
and the divisibility of x is the same as that of z.
For 7:
Since 10 × 5 ≡ 10 × (−2) ≡ 1 (mod 7) we can do the following:
Representing x as
so x is divisible by 7 if and only if y − 2z is divisible by 7.
Radix
In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system the radix is ten, because it uses the ten digits from 0 through 9.In any numeral...
, and they are all different, this article presents rules and examples only for decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
numbers.
Divisibility rules for numbers 1–20
The rules given below transform a given number into a generally smaller number, while preserving divisibility by the divisor of interest. Therefore, unless otherwise noted, the resulting number should be evaluated for divisibility by the same divisor. In some cases the process can be iterated until the divisibility is obvious; for others (such as examining the last n digits) the result must be examined by other means.For divisors with multiple rules, the rules are generally ordered first for those appropriate for numbers with many digits, then those useful for numbers with fewer digits.
Note: To test divisibility by any number that can be expressed as 2n or 5n, in which n is a positive integer, just examine the last n digits.
| Divisor | Divisibility condition | Examples |
|---|---|---|
| 1 | Automatic. | Any integer is divisible by 1. |
| 2 | The last digit is even (0, 2, 4, 6, or 8). | 1,294: 4 is even. |
| 3 | Sum the digits. | 405 → 4 + 0 + 5 = 9 and 636 → 6 + 3 + 6 = 15 which both are clearly divisible by 3. 16,499,205,854,376 → 1+6+4+9+9+2+0+5+8+5+4+3+7+6 sums to 69 → 6 + 9 = 15 → 1 + 5 = 6, which is clearly divisible by 3. |
| Subtract the quantity of the digits 2, 5 and 8 in the number from the quantity of the digits 1, 4 and 7 in the number. | Using the example above: 16,499,205,854,376 has four of the digits 1, 4 and 7; four of the digits 2, 5 and 8; ∴ Since 4 − 4 = 0 is a multiple of 3, the number 16,499,205,854,376 is divisible by 3. | |
| 4 | Examine the last two digits. | 40832: 32 is divisible by 4. |
| If the tens digit is even, and the ones digit is 0, 4, or 8. If the tens digit is odd, and the ones digit is 2 or 6. |
40832: 3 is odd, and the last digit is 2. | |
| Twice the tens digit, plus the ones digit. | 40832: 2 × 3 + 2 = 8, which is divisible by 4. | |
| 5 | The last digit is 0 or 5. | 495: the last digit is 5. |
| 6 | It is divisible by 2 and by 3. | 1,458: 1 + 4 + 5 + 8 = 18, so it is divisible by 3 and the last digit is even, hence the number is divisible by 6. |
| 7 | Form the alternating sum of blocks of three from right to left. | 1,369,851: 851 − 369 + 1 = 483 = 7 × 69 |
| Subtract 2 times the last digit from the rest. (Works because 21 is divisible by 7.) | 483: 48 − (3 × 2) = 42 = 7 × 6. | |
| Or, add 5 times the last digit to the rest. (Works because 49 is divisible by 7.) | 483: 48 + (3 × 5) = 63 = 7 × 9. | |
| Or, add 3 times the first digit to the next. (This works because 10a + b − 7a = 3a + b − last number has the same remainder) | 483: 4×3 + 8 = 20 remainder 6, 6×3 + 3 = 21. | |
| Multiply each digit (from right to left) by the digit in the corresponding position in this pattern (from left to right): 1, 3, 2, -1, -3, -2 (repeating for digits beyond the hundred-thousands place). Then sum the results. | 483595: (4 × (-2)) + (8 × (-3)) + (3 × (-1)) + (5 × 2) + (9 × 3) + (5 × 1) = 7. | |
| 8 | ||
| If the hundreds digit is odd, examine the number obtained by the last two digits plus 4. | 352: 52 + 4 = 56. | |
| Add the last digit to twice the rest. | 56: (5 × 2) + 6 = 16. | |
| Examine the last three digits | 34152: Examine divisibility of just 152: 19 × 8 | |
| Add four times the hundreds digit to twice the tens digit to the ones digit. | 34152: 4 × 1 + 5 × 2 + 2 = 16 | |
| 9 | Sum the digits. | 2,880: 2 + 8 + 8 + 0 = 18: 1 + 8 = 9. |
| 10 10 (number) 10 is an even natural number following 9 and preceding 11.-In mathematics:Ten is a composite number, its proper divisors being , and... |
The last digit is 0. | 130: the last digit is 0. |
| 11 11 (number) 11 is the natural number following 10 and preceding 12.Eleven is the first number which cannot be counted with a human's eight fingers and two thumbs additively. In English, it is the smallest positive integer requiring three syllables and the largest prime number with a single-morpheme name... |
Form the alternating sum of the digits. | 918,082: 9 − 1 + 8 − 0 + 8 − 2 = 22. |
| Add the digits in blocks of two from right to left. | 627: 6 + 27 = 33. | |
| Subtract the last digit from the rest. | 627: 62 − 7 = 55. | |
| If the number of digits is even, add the first and subtract the last digit from the rest. | 918,082: the number of digits is even (6) → 1808 + 9 − 2 = 1815: 81 + 1 − 5 = 77 = 7 × 11 | |
| If the number of digits is odd, subtract the first and last digit from the rest. | 14,179: the number of digits is odd (5) → 417 − 1 − 9 = 407 = 37 × 11 | |
| 12 12 (number) 12 is the natural number following 11 and preceding 13.The word "twelve" is the largest number with a single-morpheme name in English. Etymology suggests that "twelve" arises from the Germanic compound twalif "two-leftover", so a literal translation would yield "two remaining [after having ten... |
It is divisible by 3 and by 4. | 324: it is divisible by 3 and by 4. |
| Subtract the last digit from twice the rest. | 324: 32 × 2 − 4 = 60. | |
| 13 13 (number) 13 is the natural number after 12 and before 14. It is the smallest number with eight letters in its name spelled out in English. It is also the first of the teens – the numbers 13 through 19 – the ages of teenagers.... |
Form the alternating sum of blocks of three from right to left. | 2,911,272: −2 + 911 − 272 = 637 |
| Add 4 times the last digit to the rest. | 637: 63 + 7 × 4 = 91, 9 + 1 × 4 = 13. | |
| Multiply each digit (from right to left) by the digit in the corresponding position in this pattern (from left to right): -3, -4, -1, 3, 4, 1 (repeating for digits beyond the hundred-thousands place). Then sum the results.. | 30,747,912: (2 × (-3)) + (1 × (-4)) + (9 × (-1)) + (7 × 3) + (4 × 4) + (7 × 1) + (0 × (-3)) + (3 × (-4)) = 13. | |
| 14 14 (number) 14 is the natural number following 13 and preceding 15.In speech, the numbers 14 and 40 are often confused. When carefully enunciated, they differ in which syllable is stressed: 14 vs 40... |
It is divisible by 2 and by 7. | 224: it is divisible by 2 and by 7. |
| Add the last two digits to twice the rest. The answer must be divisible by 14. | 364: 3 × 2 + 64 = 70. | |
| 15 15 (number) 15 is the natural number following 14 and preceding 16. In English, it is the smallest natural number with seven letters in its spelled name.... |
It is divisible by 3 and by 5. | 390: it is divisible by 3 and by 5. |
| 16 16 (number) 16 is the natural number following 15 and preceding 17. 16 is a composite number, and a square number, being 42 = 4 × 4. It is the smallest number with exactly five divisors, its proper divisors being , , and .... |
If the thousands digit is even, examine the number formed by the last three digits. | 254,176: 176. |
| If the thousands digit is odd, examine the number formed by the last three digits plus 8. | 3,408: 408 + 8 = 416. | |
| Add the last two digits to four times the rest. | 176: 1 × 4 + 76 = 80. 1168: 11 × 4 + 68 = 112. |
|
| Examine the last four digits. | 157,648: 7,648 = 428 × 16. | |
| 17 17 (number) 17 is the natural number following 16 and preceding 18. It is prime.In spoken English, the numbers 17 and 70 are sometimes confused because they sound similar. When carefully enunciated, they differ in which syllable is stressed: 17 vs 70... |
Subtract 5 times the last digit from the rest. | 221: 22 − 1 × 5 = 17. |
| 18 18 (number) 18 is the natural number following 17 and preceding 19.In speech, the numbers 18 and 80 are sometimes confused. When carefully enunciated, they differ in which syllable is stressed: 18 vs 80 . However, in dates such as 1864, or when contrasting numbers in the teens, such as 17, 18, 19, the stress... |
It is divisible by 2 and by 9. | 342: it is divisible by 2 and by 9. |
| 19 19 (number) 19 is the natural number following 18 and preceding 20. It is a prime number.In English speech, the numbers 19 and 90 are often confused. When carefully enunciated, they differ in which syllable is stressed: 19 vs 90... |
Add twice the last digit to the rest. | 437: 43 + 7 × 2 = 57. |
| 20 20 (number) 20 is the natural number following 19 and preceding 21. A group of twenty units may also be referred to as a score.-In mathematics:*20 is the basis for vigesimal number systems.... |
It is divisible by 10, and the tens digit is even. | 360: is divisible by 10, and 6 is even. |
| If the number formed by the last two digits is divisible by 20. | 480: 80 is divisible by 20. |
Divisibility by 2
First, take any even number (for this example it will be 376) and note the last digit in the number, discarding the other digits. Then take that digit (6) while ignoring the rest of the number and determine if it is divisible by 2. If it is divisible by 2, then the original number is divisible by 2.Example
- 376 (The original number)
-
376 (Take the last digit) - 6 ÷ 2 = 3 (Check to see if the last digit is divisible by 2)
- 376 ÷ 2 = 188 (If the last digit is divisible by 2, then the whole number is divisible by 2)
Divisibility by 3
First, take any number (for this example it will be 492) and add together each digit in the number (4 + 9 + 2 = 15). Then take that sum (15) and determine if it is divisible by 3. The original number is divisible by 3 if and only if the final number is divisible by 3.If a number is a multiplication of 3 consecutive numbers then that number is always divisible by 3. This is useful for when the number takes the form of (n × (n − 1) × (n + 1))
Ex.
- 492 (The original number)
- 4 + 9 + 2 = 15 (Add each individual digit together)
- 15 is divisible by 3 at which point we can stop. Alternatively we can continue using the same method if the number is still too large:
- 1 + 5 = 6 (Add each individual digit together)
- 6 ÷ 3 = 2 (Check to see if the number received is divisible by 3)
- 492 ÷ 3 = 164 (If the number obtained by using the rule is divisible by 3, then the whole number is divisible by 3)
Ex.
- 336 (The original number)
- 6 × 7 × 8 = 336
- 336 ÷ 3 = 112
Divisibility by 4
The basic rule for divisibility by 4 is that if the number formed by the last two digits in a number is divisible by 4, the original number is divisible by 4; this is because 100 is divisible by 4 and so adding hundreds, thousands, etc. is simply adding another number that is divisible by 4. If any number ends in a two digit number that you know is divisible by 4 (e.g. 24, 04, 08, etc.), then the whole number will be divisible by 4 regardless of what is before the last two digits.Alternatively, one can simply divide the number by 2, and then check the result to find if it is divisible by 2. If it is, the original number is divisible by 4. In addition, the result of this test is the same as the original number divided by 4.
Ex.
General rule
- 2092 (The original number)
-
2092 (Take the last two digits of the number, discarding any other digits) - 92 ÷ 4 = 23 (Check to see if the number is divisible by 4)
- 2092 ÷ 4 = 523 (If the number that is obtained is divisible by 4, then the original number is divisible by 4)
Alternative example
- 1720 (The original number)
- 1720 ÷ 2 = 860 (Divide the original number by 2)
- 860 ÷ 2 = 430 (Check to see if the result is divisible by 2)
- 1720 ÷ 4 = 430 (If the result is divisible by 2, then the original number is divisible by 4)
Divisibility by 5
Divisibility by 5 is easily determined by checking the last digit in the number (475), and seeing if it is either 0 or 5. If the last number is either 0 or 5, the entire number is divisible by 5.If the last digit in the number is 0, then the result will be the remaining digits multiplied by 2. For example, the number 40 ends in a zero (0), so take the remaining digits (4) and multiply that by two (4 × 2 = 8). The result is the same as the result of 40 divided by 5(40/5 = 8).
If the last digit in the number is 5, then the result will be the remaining digits multiplied by two (2), plus one (1). For example, the number 125 ends in a 5, so take the remaining digits (12), multiply them by two (12 × 2 = 24), then add one (24 + 1 = 25). The result is the same as the result of 125 divided by 5 (125/5=25).
Ex.
If the last digit is 0
- 110 (The original number)
-
110 (Take the last digit of the number, and check if it is 0 or 5) - 11
0(If it is 0, take the remaining digits, discarding the last) - 11 × 2 = 22 (Multiply the result by 2)
- 110 ÷ 5 = 22 (The result is the same as the original number divided by 5)
If the last digit is 5
- 85 (The original number)
-
85 (Take the last digit of the number, and check if it is 0 or 5) - 8
5(If it is 5, take the remaining digits, discarding the last) - 8 × 2 = 16 (Multiply the result by 2)
- 16 + 1 = 17 (Add 1 to the result)
- 85 ÷ 5 = 17 (The result is the same as the original number divided by 5)
Divisibility by 6
Divisibility by 6 is determined by checking the original number to see if it is both an even number (divisible by 2) and divisible by 3. This is the best test to use.Alternatively, one can check for divisibility by six by taking the number (246), dropping the last digit in the number (24
If the number is divisible by six, take the original number (246) and divide it by two (246 ÷ 2 = 123). Then, take that result and divide it by three (123 ÷ 3 = 41). This result is the same as the original number divided by six (246 ÷ 6 = 41).
Ex.
General rule
- 324 (The original number)
- 324 ÷ 3 = 108 (Check to see if the original number is divisible by 3)
- 324 ÷ 2 = 162 OR 108 ÷ 2 = 54 (Check to see if either the original number or the result of the previous equation is divisible by 2)
- 324 ÷ 6 = 54 (If either of the tests in the last step are true, then the original number is divisible by 6. Also, the result of the second test returns the same result as the original number divided by 6)
Finding a remainder of a number when divided by 6
6 − (1, −2, −2, −2, −2, and −2 goes on for the rest) No period.
Minimum magnitude sequence
(1, 4, 4, 4, 4, and 4 goes on for the rest)
Positive sequence
Multiply the right most digit by the left most digit in the sequence and multiply the second right most digit by the second left most digit in the sequence and so on. Next, compute the sum of all the values and take the remainder on division by 6.
Example: What is the remainder when 1036125837 is divided by 6?
Multiplication of the rightmost digit = 1 × 7 = 7
Multiplication of the second rightmost digit = 3 × −2 = −6
Third rightmost digit = −16
Fourth rightmost digit = −10
Fifth rightmost digit = −4
Sixth rightmost digit = −2
Seventh rightmost digit = −12
Eighth rightmost digit = −6
Ninth rightmost digit = 0
Tenth rightmost digit = −2
Sum = −51
−51 modulo 6 = 3
Remainder = 3
Divisibility by 7
Divisibility by 7 can be tested by a recursive method. A number of the form 10x + y is divisible by 7 if and only if x − 2y is divisible by 7. In other words, subtract twice the last digit from the number formed by the remaining digits. Continue to do this until a small number (below 20 in absolute valueAbsolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
) is obtained. The original number is divisible by 7 if and only if the number obtained using this procedure is divisible by 7. For example, the number 371: 37 − (2×1) = 37 − 2 = 35; 3 − (2 × 5) = 3 − 10 = −7; thus, since −7 is divisible by 7, 371 is divisible by 7.
Another method is multiplication by 3. A number of the form 10x + y has the same remainder when divided by 7 as 3x + y. So get the leftmost digit of the original number, multiply by 3, add the next digit, get the remainder by 7, and continue from the beginning: multiply by 3, add the next digit, etc. For example, the number 371: 3×3 + 7 = 16 remainder 2, and 2×3 + 1 = 7. This method can be used to find the remainder of division by 7.
A more complicated algorithm for testing divisibility by 7 uses the fact that 100 ≡ 1, 101 ≡ 3, 102 ≡ 2, 103 ≡ 6, 104 ≡ 4, 105 ≡ 5, 106 ≡ 1, ... (mod 7). Take each digit of the number (371) in reverse order (173), multiplying them successively by the digits 1, 3, 2, 6, 4, 5, repeating with this sequence of multipliers as long as necessary (1, 3, 2, 6, 4, 5, 1, 3, 2, 6, 4, 5, ...), and adding the products (1×1 + 7×3 + 3×2 = 1 + 21 + 6 = 28). The original number is divisible by 7 if and only if the number obtained using this procedure is divisible by 7 (hence 371 is divisible by 7 since 28 is).
This method can be simplified by removing the need to multiply. All it would take with this simplification is to memorise the sequence above (132645...), and to add and subtract, but always working with one-digit numbers.
The simplification goes as follows:
- Take for instance the number 371
- Change all occurrences of a 7, 8 or 9 into 0, 1 or 2 respectively. In this example, we get: 301. This second step may be skipped, except for the left most digit, but following it may facilitate calculations later on.
- Now convert the first digit (3) into the following digit in the sequence 13264513... In our example, 3 becomes 2.
- Add the result in the previous step (2) to the second digit of the number, and substitute the result for both digits, leaving all remaining digits unmodified: 2 + 0 = 2. So 301 becomes 21.
- Repeat the procedure until you have a recognisable multiple of 7, or to make sure, a number between 0 and 6. So, starting from 21 (which is anyway a recognisable multiple of 7) take the first digit (2) and convert it into the following in the sequence above: 2 becomes 6. Then add this to the second digit: 6 + 1 = 7.
- If at any point the first digit is an 8 or a 9, these should become 1, or 2 respectively. But if it is a 7 it should become 0, only if no other digits follow. Otherwise, it should simply be dropped. This is because that 7 would have become 0, and numbers with at least two digits before the decimal dot do not begin with 0, which is useless. According to this, our 7 becomes 0.
If through this procedure you obtain a 0 or any recognisable multiple of 7, then the original number is a multiple of 7. If you obtain any number from 1 to 6, that will indicate how much you should subtract from the original number to get a multiple of 7. In other words, you will find the remainder
Remainder
In arithmetic, the remainder is the amount "left over" after the division of two integers which cannot be expressed with an integer quotient....
of dividing the number by 7. For example take the number 186:
- First, change the 8 into a 1:
Now we have a number lower than 7, and this number (4) is the remainder of dividing 186/7. So 186 minus 4, which is 182, must be a multiple of 7.
Note: The reason why this works is that if we have: a+b=c and b is a multiple of any given number n, then a and c will necessarily produce the same remainder when divided by n. In other words, in 2 + 7 = 9, 7 is divisible by 7. So 2 and 9 must have the same reminder when divided by 7. The remainder is 2.
Therefore, if a number n is a multiple of 7 (i.e.: the remainder of n/7 is 0), then adding (or subtracting) multiples of 7 cannot possibly change that property.
What this procedure does, as explained above for most divisibility rules, is simply subtract little by little multiples of 7 from the original number until reaching a number that is small enough for us to remember if it is a multiple of 7 or not. If 1 becomes a 3 in the following decimal position, that is just the same as converting 10×10n into a 3×10n. And that is actually the same as subtracting 7×10n (clearly a multiple of 7) from 10×10n.
Similarly, when you turn a 3 into a 2 in the following decimal position, you are turning 30×10n into 2×10n, which is the same as subtracting 30×10n−28×10n, and this is again subtracting a multiple of 7. The same reason applies for all the remaining conversions:
- 20×10n − 6×10n=14×10n
- 60×10n − 4×10n=56×10n
- 40×10n − 5×10n=35×10n
- 50×10n − 1×10n=49×10n
First method example
1050 → 105 − 0=105 → 10 − 10 = 0. ANSWER: 1050 is divisible by 7.
Second method example
1050 → 0501 (reverse) → 0×1 + 5×3 + 0×2 + 1×6 = 0 + 15 + 0 + 6 = 21 (multiply and add). ANSWER: 1050 is divisible by 7.
Vedic method of divisibility by osculation
Divisibility by seven can be tested by multiplication by the Ekhādika. Convert the divisor seven to the nines family by multiplying by seven. 7×7=49. Add one, drop the units digit and, take the 5, the Ekhādika, as the multiplier. Start on the right. Multiply by 5, add the product to the next digit to the left. Set down that result on a line below that digit. Repeat that method of multiplying the units digit by five and adding that product to the number of tens. Add the result to the next digit to the left. Write down that result below the digit. Continue to the end. If the end result is zero or a multiple of seven, then yes, the number is divisible by seven. Otherwise, it is not. This follows the Vedic ideal, one-line notation.
Vedic method example:
Is 438,722,025 divisible by seven? Multiplier = 5.
4 3 8 7 2 2 0 2 5
42 37 46 37 6 40 37 27
YES
Pohlman–Mass method of divisibility by 7
The Pohlman–Mass method provides a quick solution that can determine if most integers are divisible by seven in three steps or less. This method could be useful in a mathematics competition such as MATHCOUNTS, where time is a factor to determine the solution without a calculator in the Sprint Round.
Step A:
If the integer is 1,000 or less, subtract twice the last digit from the number formed by the remaining digits. If the result is a multiple of seven, then so is the original number (and vice versa). For example:
112 -> 11 − (2×2) = 11 − 4 = 7 YES
98 -> 9 − (8×2) = 9 − 16 = −7 YES
634 -> 63 − (4×2) = 63 − 8 = 55 NO
Because 1,001 is divisible by seven, an interesting pattern develops for repeating sets of 1, 2, or 3 digits that form 6-digit numbers (leading zeros are allowed) in that all such numbers are divisible by seven. For example:
001 001 = 1,001 / 7 = 143
010 010 = 10,010 / 7 = 1,430
011 011 = 11,011 / 7 = 1,573
100 100 = 100,100 / 7 = 14,300
101 101 = 101,101 / 7 = 14,443
110 110 = 110,110 / 7 = 15,730
01 01 01 = 10,101 / 7 = 1,443
10 10 10 = 101,010 / 7 = 14,430
111,111 / 7 = 15,873
222,222 / 7 = 31,746
999,999 / 7 = 142,857
576,576 / 7 = 82,368
For all of the above examples, subtracting the first thee digits from the last three results in a multiple of seven. Notice that leading zeros are permitted to form a 6-digit pattern.
This phenomenon forms the basis for Steps B and C.
Step B:
If the integer is between 1,001 and one million, find a repeating pattern of 1, 2, or 3 digits that forms a 6-digit number that is close to the integer (leading zeros are allowed and can help you visualize the pattern). If the positive difference is less than 1,000, apply Step A. This can be done by subtracting the first three digits from the last three digits. For example:
341,355 − 341,341 = 14 -> 1 − (4×2) = 1 − 8 = −7 YES
67,326 − 067,067 = 259 -> 25 − (9×2) = 25 − 18 = 7 YES
The fact that 999,999 is a multiple of 7 can be used for determining divisibility of integers larger than one million by reducing the integer to a 6-digit number that can be determined using Step B. This can be done easily by adding the digits left of the first six to the last six and follow with Step A.
Step C:
If the integer is larger than one million, subtract the nearest multiple of 999,999 and then apply Step B. For even larger numbers, use larger sets such as 12-digits (999,999,999,999) and so on. Then, break the integer into a smaller number that can be solved using Step B. For example:
22,862,420 − (999,999 × 22) = 22,862,420 − 21,999,978 -> 862,420 + 22 = 862,442
862,442 -> 862 − 442 (Step B) = 420 -> 42 − (0×2) (Step A) = 42 YES
This allows adding and subtracting alternating sets of three digits to determine divisibility by seven. Understanding these patterns allows you to quickly calculate divisibility of seven as seen in the following examples:
Pohlman–Mass method of divisibility by 7, examples:
Is 98 divisible by seven?
98 -> 9 − (8×2) = 9 − 16 = −7 YES (Step A)
Is 634 divisible by seven?
634 -> 63 − (4×2) = 63 − 8 = 55 NO (Step A)
Is 355,341 divisible by seven?
355,341 − 341,341 = 14,000 (Step B) -> 014 − 000 (Step B) -> 14 = 1 − (4×2) (Step A) = 1 − 8 = −7 YES
Is 42,341,530 divisible by seven?
42,341,530 -> 341,530 + 42 = 341,572 (Step C)
341,572 − 341,341 = 231 (Step B)
231 -> 23 − (1×2) = 23 − 2 = 21 YES (Step A)
Using quick alternating additions and subtractions:
42,341,530 -> 530 − 341 = 189 + 42 = 231 -> 23 − (1×2) = 21 YES
Multiplication by 3 method of divisibility by 7, examples:
Is 98 divisible by seven?
98 -> 9 remainder 2 -> 2×3 + 8 = 14 YES
Is 634 divisible by seven?
634 -> 6×3 + 3 = 21 -> remainder 0 -> 0×3 + 4 = 4 NO
Is 355,341 divisible by seven?
3 * 3 + 5 = 14 -> remainder 0 -> 0×3 + 5 = 5 -> 5×3 + 3 = 18 -> remainder 4 -> 4×3 + 4 = 16 -> remainder 2 -> 2×3 + 1 = 7 YES
Find remainder of 1036125837 divided by 7
1×3 + 0 = 3
3×3 + 3 = 12 remainder 5
5×3 + 6 = 21 remainder 0
0×3 + 1 = 1
1×3 + 2 = 5
5×3 + 5 = 20 remainder 6
6×3 + 8 = 26 remainder 5
5×3 + 3 = 18 remainder 4
4×3 + 7 = 19 remainder 5
Answer is 5
Finding remainder of a number when divided by 7
7 − (1, 3, 2, −1, −3, −2, cycle repeats for the next six digits) Period: 6 digits.
Recurring numbers: 1, 3, 2, −1, −3, −2
Minimum magnitude sequence
(1, 3, 2, 6, 4, 5, cycle repeats for the next six digits) Period: 6 digits.
Recurring numbers: 1, 3, 2, 6, 4, 5
Positive sequence
Multiply the right most digit by the left most digit in the sequence and multiply the second right most digit by the second left most digit in the sequence and so on and so for. Next, compute the sum of all the values and take the modulus of 7.
Example: What is the remainder when 1036125837 is divided by 7?
Multiplication of the rightmost digit = 1 × 7 = 7
Multiplication of the second rightmost digit = 3 × 3 = 9
Third rightmost digit = 8 × 2 = 16
Fourth rightmost digit = 5 × −1 = −5
Fifth rightmost digit = 2 × −3 = −6
Sixth rightmost digit = 1 × −2 = −2
Seventh rightmost digit = 6 × 1 = 6
Eighth rightmost digit = 3 × 3 = 9
Ninth rightmost digit = 0
Tenth rightmost digit = 1 × −1 = −1
Sum = 33
33 modulus 7 = 5
Remainder = 5
Digit pair method of divisibility by 7
This method uses 1, −3, 2 pattern on the digit pairs. That is, the divisibility of any number by seven can be tested by first separating the number into digit pairs, and then applying the algorithm on three digit pairs (six digits). When the number is smaller than six digits, then fill zero’s to the right side until there are six digits. When the number is larger than six digits, then repeat the cycle on the next six digit group and then add the results. Repeat the algorithm until the result is a small number. The original number is divisible by seven if and only if the number obtained using this algorithm is divisible by seven. This method is especially suitable for large numbers.
Example 1:
The number to be tested is 157514.
First we separate the number into three digit pairs: 15, 75 and 14.
Then we apply the algorithm: 1 × 15 − 3 × 75 + 2 × 14 = 182
Because the resulting 182 is less than six digits, we add zero’s to the right side until it is six digits.
Then we apply our algorithm again: 1 × 18 − 3 × 20 + 2 × 0 = −42
The result −42 is divisible by seven, thus the original number 157514 is divisible by seven!
Example 2:
The number to be tested is 15751537186.
(1 × 15 − 3 × 75 + 2 × 15) + (1 × 37 − 3 × 18 + 2 × 60) = −180 + 103 = −77
The result −77 is divisible by seven, thus the original number 15751537186 is divisible by seven!
Divisibility by 13
Remainder Test13 (1, −3, −4, −1, 3, 4, cycle goes on.)
If you are not comfortable with negative numbers, then use this sequence. (1, 10, 9, 12, 3, 4)
Multiply the right most digit of the number with the left most number in the sequence shown above and the second right most digit to the second left most digit of the number in the sequence. The cycle goes on.
Example: What is the remainder when 321 is divided by 13?
Using the first sequence,
Ans: 1 × 1 + 2 × −3 + 3 × −4 = 9
Remainder = −17 mod 13 = 9
Example: What is the remainder when 1234567 is divided by 13?
Using the second sequence,
Answer: 7 × 1 + 6 × 10 + 5 × 9 + 4 × 12 + 3 × 3 + 2 × 4 + 1 × 1 = 178 mod 13 = 9
Remainder = 9
Beyond 20
Divisibility properties can be determined in two ways, depending on the type of the divisor.Composite divisors
A number is divisible by a given divisor if it is divisible by the highest power of each of its primePrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
factors. For example, to determine divisibility by 24, check divisibility by 8 and by 3. Note that checking 4 and 6, or 2 and 12, would not be sufficient. A table of prime factors
Table of prime factors
The tables contain the prime factorization of the natural numbers from 1 to 1000.When n is a prime number, the prime factorization is just n itself, written in bold below.The number 1 is called a unit...
may be useful.
A composite
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
divisor may also have a rule formed using the same procedure as for a prime divisor, given below, with the caveat that the manipulations involved may not introduce any factor which is present in the divisor. For instance, one can not make a rule for 14 that involves multiplying the equation by 7. This is not an issue for prime divisors because they have no smaller factors.
Prime divisors
The goal is to find an inverse to 10 modulo the prime (not 2 or 5) and use that as a multiplier to make the divisibility of the original number by that prime depend on the divisibility of the new (usually smaller) number by the same prime.Using 17 as an example, since 10 × (−5) = −50 = 1 mod 17, we get the rule for using y − 5x in the table above. In fact, this rule for prime divisors besides 2 and 5 is really a rule
for divisibility by any integer relatively prime to 10 (including 21 and 27; see tables below). This is why the last divisibility condition in the tables above and below for any number relatively prime to 10 has the same kind of form (add or subtract some multiple of the last digit from the rest of the number).
Notable examples
The following table provides rules for a few more notable divisors:| Divisor | Divisibility condition | Examples |
|---|---|---|
| 21 21 (number) 21 is the natural number following 20 and preceding 22.-In mathematics:Twenty-one is the fifth discrete Semiprime and the second in the family. With 22 it forms the second discrete Semiprime pair... |
Subtract twice the last digit from the rest. | 168: 16 − (8×2) = 0, 168 is divisible. 1050: 105 − (0×2) = 105, 10 − (5×2) = 0, 1050 is divisible. |
| 23 23 (number) 23 is the natural number following 22 and preceding 24.- In mathematics :Twenty-three is the ninth prime number, the smallest odd prime that is not a twin prime. Twenty-three is also the fifth factorial prime, the third Woodall prime... |
Add 7 times the last digit to the rest. | |
| 25 25 (number) 25 is the natural number following 24 and preceding 26.-In mathematics:It is a square number, being 5² = 5 × 5. It is the smallest square that is also a sum of two squares: 25 = 3² + 4²... |
The number formed by the last two digits is divisible by 25. | 134,250: 50 is divisible by 25. |
| 27 27 (number) 27 is the natural number following 26 and preceding 28.- In mathematics :Twenty-seven is a perfect cube, being 33 = 3 × 3 × 3. 27 is also 23 . There are exactly 27 straight lines on a smooth cubic surface, which give a basis of the fundamental representation of the E6 Lie algebra... |
Sum the digits in blocks of three from right to left. If the result is divisible by 27, then the number is divisible by 27. | 2,644,272: 2 + 644 + 272 = 918 = 27×34. |
| Subtract 8 times the last digit from the rest. | 621: 62 − (1×8) = 54. | |
| 29 29 (number) 29 is the natural number following 28 and preceding 30.-In mathematics:It is the tenth prime number, and also the fourth primorial prime. It forms a twin prime pair with thirty-one, which is also a primorial prime. Twenty-nine is also the sixth Sophie Germain prime. It is also the sum of three... |
Add three times the last digit to the rest. | 261: 1×3 = 3; 3 + 26 = 29 |
| 31 31 (number) 31 is the natural number following 30 and preceding 32.- In mathematics :Thirty-one is the third Mersenne prime as well as the fourth primorial prime, and together with twenty-nine, another primorial prime, it comprises a twin prime. As a Mersenne prime, 31 is related to the perfect number 496,... |
Subtract three times the last digit from the rest. | 837: 83 − 3×7 = 62 |
| 32 32 (number) 32 is the natural number following 31 and preceding 33.-In mathematics:32 is the smallest number n with exactly 7 solutions to the equation φ = n... |
||
| If the ten thousands digit is odd, examine the number formed by the last four digits plus 16. | 254,176: 4176+16 = 4192. | |
| Add the last two digits to 4 times the rest. | 1,312: (13×4) + 12 = 64. | |
| 33 33 (number) 33 is the natural number following 32 and preceding 34.-In mathematics:33 is the largest positive integer that cannot be expressed as a sum of different triangular numbers. It is also the smallest odd repdigit that is not a prime number.33 is the eighth distinct semiprime comprising the prime... |
Add 10 times the last digit to the rest; it has to be divisible by 3 and 11. | 627: 62 + 7 × 10 = 132, 13 + 2 × 10 = 33. |
| Add the digits in blocks of two from right to left. | 2,145: 21 + 45 = 66. | |
| 35 35 (number) 35 is the natural number following 34 and preceding 36.- In mathematics :35 is the sum of the first five triangular numbers, making it a tetrahedral number.... |
Number must be divisible by 7 ending in 0 or 5. | |
| 37 37 (number) 37 is the natural number following 36 and preceding 38.-In mathematics:It is a prime number, the fifth lucky prime, the first irregular prime, the third unique prime and the third cuban prime of the form... |
Take the digits in blocks of three from right to left and add each block, just as for 27. | 2,651,272: 2 + 651 + 272 = 925. 925 = 37×25. |
| Subtract 11 times the last digit from the rest. | 925: 92 − (5×11) = 37. | |
| 39 39 (number) 39 is the natural number following 38 and preceding 40.- In mathematics :Thirty-nine is the sum of five consecutive primes and the sum of the first three powers of 3... |
Add 4 times the last digit to the rest. | 351: 1 × 4 = 4; 4 + 35 = 39 |
| 41 41 (number) 41 is the natural number following 40 and preceding 42.-In mathematics:Forty-one is the 13th smallest prime number. The next is forty-three, with which it comprises a twin prime... |
Subtract 4 times the last digit from the rest. | 738: 73 − 8 × 4 = 41. |
| 43 43 (number) 43 is the natural number following 42 and preceding 44.- In mathematics :Forty-three is the 14th smallest prime number. The previous is forty-one, with which it comprises a twin prime, and the next is forty-seven. 43 is the smallest prime that is not a Chen prime... |
Add 13 times the last digit to the rest. | 36,249: 3624 + 9 × 13 = 3741, 374 + 1 × 13 = 387, 38 + 7 × 13 = 129, 12 + 9 × 13 = 129 = 43 × 3. |
| Subtract 30 times the last digit from the rest. | 36,249: 3624 - 9 × 30 = 3354, 335 - 4 × 30 = 215 = 43 × 5. |
|
| 45 45 (number) 45 is the natural number following 44 and followed by 46.- In mathematics :Forty-five is a triangular number, a hexagonal and 16-gonal number, a Kaprekar number, and a Harshad number.... |
The number must be divisible by 9 ending in 0 or 5. | 495: 4 + 9 + 5 = 18, 1 + 8 = 9; (495 is divisible by both 5 and 9.) |
| 47 47 (number) 47 is the natural number following 46 and preceding 48.-In mathematics:Forty-seven is the fifteenth prime number, a safe prime, the thirteenth supersingular prime, and the sixth Lucas prime. Forty-seven is a highly cototient number... |
Subtract 14 times the last digit from the rest. | 1,642,979: 164297 − 9 × 14 = 164171, 16417 − 14 = 16403, 1640 − 3 × 14 = 1598, 159 − 8 × 14 = 47. |
| 49 49 (number) 49 is the natural number following 48 and preceding 50.-In mathematics:* Forty-nine is the square of seven and is therefore the fourth squared prime number.The aliquot sum of forty-nine is 8... |
Add 5 times the last digit to the rest. | 1,127: 112+(7×5)=147. 147: 14 + (7×5) = 49 |
| 50 50 (number) This article discusses the number fifty. For the year 50 CE, see 50. For other uses of 50, see 50 50 is the natural number following 49 and preceding 51.-In mathematics:... |
The last two digits are 00 or 50. | 134,250: 50. |
| 51 | Subtract 5 times the last digit to the rest. | |
| 55 55 (number) 55 is the natural number following 54 and preceding 56.-Albania:*Gazeta 55, a newspaper*Constitution law 55, a law during Communist Albania.-Mathematics:... |
Number must be divisible by 11 ending in 0 or 5. | 935: 93 − 5 = 88 or 9 + 35 = 44. |
| 59 59 (number) 59 is the natural number following 58 and preceding 60.-In mathematics:Fifty-nine is the 17th smallest prime number. The next is sixty-one, with which it comprises a twin prime. 59 is an irregular prime, a safe prime and the 14th supersingular prime. It is an Eisenstein prime with no imaginary... |
Add 6 times the last digit to the rest. | 295: 5×6 = 30; 30 + 29 = 59 |
| 61 61 (number) 61 is the natural number following 60 and preceding 62.-In mathematics:It is the 18th prime number. The previous is 59, with which it comprises a twin prime. Sixty-one is a cuban prime of the form p = / , x = y + 1.... |
Subtract 6 times the last digit from the rest. | |
| 64 64 (number) 64 is the natural number following 63 and preceding 65.-In mathematics:Sixty-four is the square of 8, the cube of 4, and the sixth power of 2. It is the smallest number with exactly seven divisors. It is the lowest positive power of two that is adjacent to neither a Mersenne prime nor a Fermat... |
The number formed by the last six digits must be divisible by 64. | |
| 65 65 (number) 65 is the natural number following 64 and preceding 66.-In mathematics:Sixty-five is the 23rd semiprime and the 3rd of the form it is an octagonal number. It is also a Cullen number... |
Number must be divisible by 13 ending in 0 or 5. | |
| 66 66 (number) 66 is the natural number following 65 and preceding 67.Usages of this number include:-Mathematics:*66 is a sphenic number, a triangular number, a hexagonal number, and a semi-meandric number... |
Number must be divisible by 6 and 11. | |
| 69 69 (number) 69 is a number following 68 and preceding 70.- In mathematics:The aliquot sum of sixty-nine is 27 within the aliquot sequence 69 being the third composite number in the 13-aliquot tree.69 is a semiprime... |
Add 7 times the last digit to the rest. | 345: 5×7 = 35; 35 + 34 = 69 |
| 71 71 (number) 71 is the natural number following 70 and preceding 72.-In mathematics:71 is the algebraic degree of Conway's constant, a remarkable number arising in the study of look-and-say sequences.... |
Subtract 7 times the last digit from the rest. | |
| 75 75 (number) 75 is the natural number following 74 and preceding 76.-In mathematics:As the sum of the first five pentagonal numbers, seventy-five is a pentagonal pyramidal number. It is also an enneagonal number.... |
Number must be divisible by 3 ending in 00, 25, 50 or 75. | 825: ends in 25 and is divisible by 3. |
| 77 77 (number) 77 is the natural number following 76 and preceding 78. Seventy-seven is the smallest positive integer requiring five syllables in English.-In mathematics:... |
Form the alternating sum of blocks of three from right to left. | 76,923: 923 - 76 = 847. |
| 79 79 (number) Seventy-nine is the natural number following 78 and preceding 80.79 may represent:-In mathematics:*An odd number*The smallest number that can't be represented as a sum of fewer than 19 fourth powers*A strictly non-palindromic number... |
Add 8 times the last digit to the rest. | 711: 1×8 = 8; 8 + 71 = 79 |
| 81 81 (number) 81 is the natural number following 80 and preceding 82.-In mathematics:Eighty-one is the square of 9 and the fourth power of 3. Like all powers of three, 81 is a perfect totient number. It is a heptagonal number and a centered octagonal number. It is also a tribonacci number, and an open meandric... |
Subtract 8 times the last digit from the rest. | |
| 89 | Add 9 times the last digit to the rest. | 801: 1×9 = 9; 80 + 9 = 89 |
| 91 91 (number) 91 is the natural number following 90 and preceding 92.-In mathematics:Ninety-one is the twenty-seventh distinct semiprime and the second of the form... |
Subtract 9 times the last digit from the rest. | |
| Form the alternating sum of blocks of three from right to left. | 5,274,997: 5 - 274 + 997 = 728 | |
| 99 99 (number) 99 is the natural number following 98 and preceding 100.-Mathematics:99 is the ninth repdigit, a palindromic number and a Kaprekar number... |
Add the digits in blocks of two from right to left. | 144,837: 14 + 48 + 37 = 99. |
| 101 101 (number) 101 is the natural number following 100 and preceding 102.It is variously pronounced "one hundred and one" / "a hundred and one", "one hundred one" / "a hundred one", and "one oh one"... |
Form the alternating sum of blocks of two from right to left. | 40,299: 4 - 2 + 99 = 101. |
| 111 111 (number) 111 is the natural number following 110 and preceding 112. It is the lowest positive integer requiring six syllables to name in American English, or seven syllables in Canadian and British English... |
Add the digits in blocks of three from right to left. | |
| 125 125 (number) 125 is the natural number following 124 and preceding 126.-In mathematics:One hundred [and] twenty-five is the cube of 5.... |
The number formed by the last three digits must be divisible by 125. | |
| 128 128 (number) 128 is the natural number following 127 and preceding 129.-In mathematics:One hundred [and] twenty-eight is the seventh power of 2. It is the largest number which cannot be expressed as the sum of any number of distinct squares... |
The number formed by the last seven digits must be divisible by 128. | |
| 143 143 (number) 143 is the natural number following 142 and preceding 144.-In mathematics:143 is the sum of three consecutive primes , as well as the sum of seven consecutive primes... |
Form the alternating sum of blocks of three from right to left. | 1,774,487: 1 - 774 + 487 = -286 |
| 256 256 (number) 256 is the natural number following 255 and preceding 257.-In mathematics:256 is a composite number, with the factorization 256 = 28, which makes it a power of two.... |
The number formed by the last eight digits must be divisible by 256. | |
| 333 | Add the digits in blocks of three from right to left. | |
| 512 512 (number) 512 is the natural number following 511 and preceding 513.512 is a power of two: 29 and the cube of 8: 83.Also, it is the eleventh Leyland number.- Special use in computers :... |
The number formed by the last nine digits must be divisible by 512. | |
| 989 | Add the last three digits to eleven times the rest. | 21758: 21 × 11 = 231; 758 + 231 = 989 |
| 999 999 (number) Nine hundred and ninety-nine is the natural number following nine hundred ninety-eight and preceding one thousand. 999 is a Harshad number and a Kaprekar number. It is the largest 3 digit whole number in base 10.... |
Add the digits in blocks of three from right to left. | |
Proof using basic algebra
Many of the simpler rules can be produced using only algebraic manipulation, creating binomialBinomial
In algebra, a binomial is a polynomial with two terms —the sum of two monomials—often bound by parenthesis or brackets when operated upon...
s and rearranging them. By writing a number as the sum of each digit times a power of 10
Positional notation
Positional notation or place-value notation is a method of representing or encoding numbers. Positional notation is distinguished from other notations for its use of the same symbol for the different orders of magnitude...
each digit's power can be manipulated individually.
Case where all digits are summed
This method works for divisors that are factors of 10 − 1 = 9.
Using 3 as an example, 3 divides 9 = 10 − 1. That means
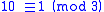(see modular arithmeticModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
). The same for all the higher powers of 10:
They are all congruentCongruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
to 1 modulo 3. Since two things that are congruent modulo 3 are either both divisible by 3 or both not, we can interchange values that are congruent modulo 3. So, in a number such as the following, we can replace all the powers of 10 by 1:
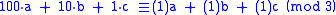
which is exactly the sum of the digits.
Case where the alternating sum of digits is used
This method works for divisors that are factors of 10 + 1 = 11.
Using 11 as an example, 11 divides 11 = 10 + 1. That means
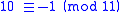. For the higher powers of 10, they are congruent to 1 for even powers and congruent to −1 for odd powers: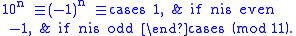Like the previous case, we can substitute powers of 10 with congruent values:
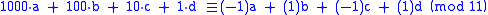
which is also the difference between the sum of digits at odd positions and the sum of digits at even positions.
Case where only the last digit(s) matter
This applies to divisors that are a factor of a power of 10. This is because sufficiently high powers of the base are multiples of the divisor, and can be eliminated.
For example, in base 10, the factors of 101 include 2, 5, and 10. Therefore, divisibility by 2, 5, and 10 only depend on whether the last 1 digit is divisible by those divisors. The factors of 102 include 4 and 25, and divisibility by those only depend on the last 2 digits.
Case where only the last digit(s) are removed
Most numbers do not divide 9 or 10 evenly, but do divide a higher power of 10n or 10n − 1. In this case the number is still written in powers of 10, but not fully expanded.
For example, 7 does not divide 9 or 10, but does divide 98, which is close to 100. Thus, proceed from
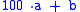
where in this case a is any integer, and b can range from 0 to 99. Next,
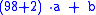
and again expanding
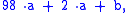
and after eliminating the known multiple of 7, the result is
which is the rule "double the number formed by all but the last two digits, then add the last two digits".
Case where the last digit(s) is multiplied by a factor
The representation of the number may also be multiplied by any number relatively prime to the divisor without changing its divisibility. After observing that 7 divides 21, we can perform the following:
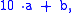
after multiplying by 2, this becomes
and then
Eliminating the 21 gives
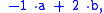
and multiplying by −1 gives
Either of the last two rules may be used, depending on which is easier to perform. They correspond to the rule "subtract twice the last digit from the rest".
Proof using modular arithmetic
This section will illustrate the basic method; all the rules can be derived following the same procedure. The following requires a basic grounding in modular arithmeticModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
; for divisibility other than by 2's and 5's the proofs rest on the basic fact that 10 mod m is invertible if 10 and m are relatively prime.
For 2n or 5n:
Only the last n digits need to be checked.
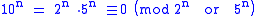
Representing x as
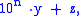
and the divisibility of x is the same as that of z.
For 7:
Since 10 × 5 ≡ 10 × (−2) ≡ 1 (mod 7) we can do the following:
Representing x as
so x is divisible by 7 if and only if y − 2z is divisible by 7.
External links
- Interactive Divisibility Lesson on these rules
- Divisibility Criteria at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Divisibility by 9 and 11 at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Divisibility by 7 at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Divisibility by 81 at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Divisibility by Three Explained
- Stupid Divisibility Tricks Divisibility rules for 2-102.