
Dixon's identity
Encyclopedia
In mathematics, Dixon's identity (or Dixon's theorem or Dixon's formula) is any of several different but closely related identities proved by A. C. Dixon, some involving finite sums of products of three binomial coefficient
s, and some evaluating a hypergeometric sum. These identities famously follow from the MacMahon Master theorem
, and can now be routinely proved by computer algorithms .

A generalization, also sometimes called Dixon's identity, is
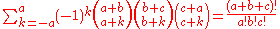
when a, b, and c are non-negative integers.
The sum on the left can be written as the terminating well-poised hypergeometric series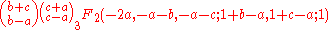
and the identity follows as a limiting case (as a tends to an integer) of
Dixon's theorem evaluating a well-poised 3F2 generalized hypergeometric series at 1, from :
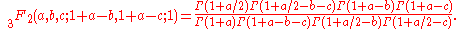
This holds for Re(1+a/2-b-c)>0. As c tends to −∞ it reduces to Kummer's formula for the hypergeometric function 2F1 at −1. Dixon's theorem can be deduced from the evaluation of the Selberg integral.
in terms of the q-Pochhammer symbol is given by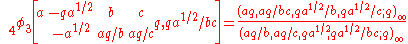
when |qa1/2/bc| < 1.
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s, and some evaluating a hypergeometric sum. These identities famously follow from the MacMahon Master theorem
MacMahon Master theorem
The MacMahon Master theorem is a result in enumerative combinatorics and linear algebra, both branches of mathematics. It was discovered by Percy MacMahon and proved in his monograph Combinatory analysis...
, and can now be routinely proved by computer algorithms .
Statements
The original identity, from , is
A generalization, also sometimes called Dixon's identity, is
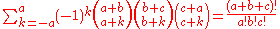
when a, b, and c are non-negative integers.
The sum on the left can be written as the terminating well-poised hypergeometric series
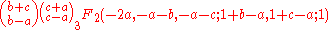
and the identity follows as a limiting case (as a tends to an integer) of
Dixon's theorem evaluating a well-poised 3F2 generalized hypergeometric series at 1, from :
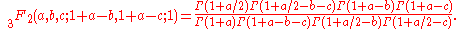
This holds for Re(1+a/2-b-c)>0. As c tends to −∞ it reduces to Kummer's formula for the hypergeometric function 2F1 at −1. Dixon's theorem can be deduced from the evaluation of the Selberg integral.
q-analogues
A q-analogue of Dixon's formula for the basic hypergeometric seriesBasic hypergeometric series
In mathematics, Heine's basic hypergeometric series, or hypergeometric q-series, are q-analog generalizations of generalized hypergeometric series, and are in turn generalized by elliptic hypergeometric series....
in terms of the q-Pochhammer symbol is given by
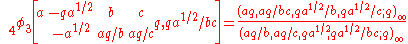
when |qa1/2/bc| < 1.

