
Dominance-based Rough Set Approach
Encyclopedia
Dominance-based rough set approach (DRSA) is an extension of rough set theory
for multi-criteria decision analysis
(MCDA), introduced by Greco, Matarazzo and Słowiński. The main change comparing to the classical rough sets is the substitution of the indiscernibility relation by a dominance relation, which permits to deal with inconsistencies typical to consideration of criteria and preference-ordered decision classes.
(sorting) is one of the problems considered within MCDA and can be stated as follows: given a set of objects evaluated by a set of criteria (attributes with preference-order domains), assign these objects to some pre-defined and preference-ordered decision classes, such that each object is assigned to exactly one class. Due to the preference ordering, improvement of evaluations of an object on the criteria should not worsen its class assignment. The sorting problem is very similar to the problem of classification, however, in the latter, the objects are evaluated by regular attributes and the decision classes are not necessarily preference ordered. The problem of multicriteria classification is also referred to as ordinal classification problem with monotonicity constraints and often appears in real-life application when ordinal
and monotone
properties follow from the domain knowledge about the problem.
As an illustrative example, consider the problem of evaluation in a high school. The director of the school wants to assign students (objects) to three classes: bad, medium and good (notice that class good is preferred to medium and medium is preferred to bad). Each student is described by three criteria: level in Physics, Mathematics and Literature, each taking one of three possible values bad, medium and good. Criteria are preference-ordered and improving the level from one of the subjects should not result in worse global evaluation (class).
As a more serious example, consider classification of bank clients, from the viewpoint of bankruptcy risk, into classes safe and risky. This may involve such characteristics as "return on equity
(ROE)", "return on investment
(ROI)" and "return on sales (ROS)". The domains of these attributes are not simply ordered but involve a preference order since, from the viewpoint of bank managers, greater values of ROE, ROI or ROS are better for clients being analysed for bankruptcy risk . Thus, these attributes are criteria. Neglecting this information in knowledge discovery
may lead to wrong conclusions.
. Formally, a DRSA decision table is a 4-tuple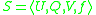 , where
, where 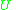 is a finite set of objects,
is a finite set of objects, 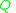 is a finite set of criteria,
is a finite set of criteria, 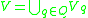 where
where  is the domain of the criterion
is the domain of the criterion 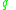 and
and 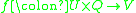 is an information function such that
is an information function such that 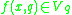 for every
for every 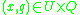 . The set
. The set 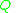 is divided into condition criteria (set
is divided into condition criteria (set 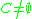 ) and the decision criterion (class)
) and the decision criterion (class) 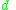 . Notice, that
. Notice, that 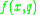 is an evaluation of object
is an evaluation of object 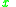 on criterion
on criterion 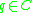 , while
, while 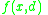 is the class assignment (decision value) of the object. An example of decision table is shown in Table 1 below.
is the class assignment (decision value) of the object. An example of decision table is shown in Table 1 below.
 is completely preorder
is completely preorder
ed by an outranking relation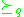 ;
; 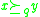 means that
means that  is at least as good as (outranks)
is at least as good as (outranks) 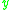 with respect to the criterion
with respect to the criterion 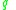 . Without loss of generality, we assume that the domain of
. Without loss of generality, we assume that the domain of 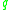 is a subset of reals
is a subset of reals
,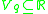 , and that the outranking relation is a simple order between real numbers
, and that the outranking relation is a simple order between real numbers 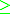 such that the following relation holds:
such that the following relation holds: 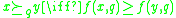 . This relation is straightforward for gain-type ("the more, the better") criterion, e.g. company profit. For cost-type ("the less, the better") criterion, e.g. product price, this relation can be satisfied by negating the values from
. This relation is straightforward for gain-type ("the more, the better") criterion, e.g. company profit. For cost-type ("the less, the better") criterion, e.g. product price, this relation can be satisfied by negating the values from 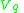 .
.
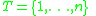 . The domain of decision criterion,
. The domain of decision criterion, 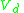 consist of
consist of 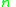 elements (without loss of generality we assume
elements (without loss of generality we assume  ) and induces a partition of
) and induces a partition of 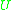 into
into 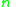 classes
classes 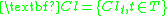 , where
, where 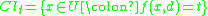 . Each object
. Each object 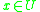 is assigned to one and only one class
is assigned to one and only one class  . The classes are preference-ordered according to an increasing order of class indices, i.e. for all
. The classes are preference-ordered according to an increasing order of class indices, i.e. for all 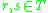 such that
such that 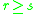 , the objects from
, the objects from 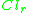 are strictly preferred to the objects from
are strictly preferred to the objects from 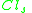 . For this reason, we can consider the upward and downward unions of classes, defined respectively, as:
. For this reason, we can consider the upward and downward unions of classes, defined respectively, as:
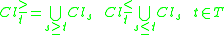
 dominates
dominates  with respect to
with respect to  , denoted by
, denoted by 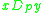 , if
, if  is better than
is better than  on every criterion from
on every criterion from  ,
, 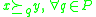 . For each
. For each 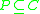 , the dominance relation
, the dominance relation 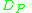 is reflexive
is reflexive
and transitive
, i.e. it is a partial pre-order
. Given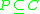 and
and 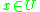 , let
, let
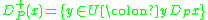
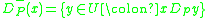
represent P-dominating set and P-dominated set with respect to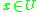 , respectively.
, respectively.
philosophy is approximation of one knowledge by another knowledge. In DRSA, the knowledge being approximated is a collection of upward and downward unions of decision classes and the "granules of knowledge" used for approximation are P-dominating and P-dominated sets.
The P-lower and the P-upper approximation of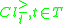 with respect to
with respect to 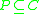 , denoted as
, denoted as 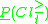 and
and  , respectively, are defined as:
, respectively, are defined as:
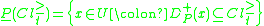
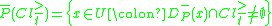
Analogously, the P-lower and the P-upper approximation of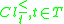 with respect to
with respect to 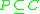 , denoted as
, denoted as 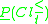 and
and 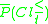 , respectively, are defined as:
, respectively, are defined as:

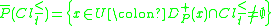
Lower approximations group the objects which certainly belong to class union (respectively
(respectively 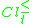 ). This certainty comes from the fact, that object
). This certainty comes from the fact, that object 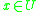 belongs to the lower approximation
belongs to the lower approximation 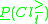 (respectively
(respectively 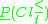 ), if no other object in
), if no other object in 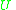 contradicts this claim, i.e. every object
contradicts this claim, i.e. every object 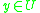 which P-dominates
which P-dominates 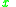 , also belong to the class union
, also belong to the class union  (respectively
(respectively 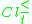 ). Upper approximations group the objects which could belong to
). Upper approximations group the objects which could belong to 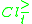 (respectively
(respectively 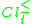 ), since object
), since object 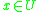 belongs to the upper approximation
belongs to the upper approximation 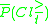 (respectively
(respectively  ), if there exist another object
), if there exist another object 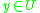 P-dominated by
P-dominated by 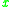 from class union
from class union  (respectively
(respectively  ).
).
The P-lower and P-upper approximations defined as above satisfy the following properties for all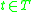 and for any
and for any  :
:
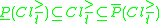
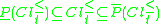
The P-boundaries (P-doubtful regions) of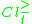 and
and 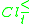 are defined as:
are defined as:
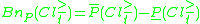


defines the quality of approximation of the partition into classes by means of the set of criteria
into classes by means of the set of criteria 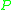 . This ratio express the relation between all the P-correctly classified objects and all the objects in the table.
. This ratio express the relation between all the P-correctly classified objects and all the objects in the table.
Every minimal subset such that
such that 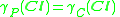 is called a reduct
is called a reduct
of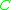 and is denoted by
and is denoted by  . A decision table may have more than one reduct. The intersection of all reducts is known as the core.
. A decision table may have more than one reduct. The intersection of all reducts is known as the core.
. The decision rules are expressions of the form if [condition] then [consequent], that represent a form of dependency between condition criteria and decision criteria. Procedures for generating decision rules from a decision table use an inducive learning principle. We can distinguish three types of rules: certain, possible and approximate. Certain rules are generated from lower approximations of unions of classes; possible rules are generated from upper approximations of unions of classes and approximate rules are generated from boundary regions.
Certain rules has the following form:
if and
and 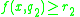 and
and 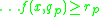 then
then 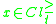
if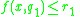 and
and 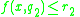 and
and 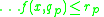 then
then 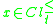
Possible rules has a similar syntax, however the consequent part of the rule has the form: could belong to
could belong to 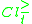 or the form:
or the form: 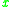 could belong to
could belong to 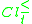 .
.
Finally, approximate rules has the syntax:
if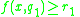 and
and 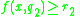 and
and 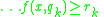 and
and 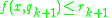 and
and 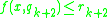 and
and 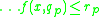
then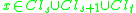
The certain, possible and approximate rules represent certain, possible and ambiguous knowledge extracted from the decision table.
Each decision rule should be minimal. Since a decision rule is an implication, by a minimal decision rule we understand such an implication that there is no other implication with an antecedent of at least the same weakness (in other words, rule using a subset of elementary conditions or/and weaker elementary conditions) and a consequent of at least the same strength (in other words, rule assigning objects to the same union or sub-union of classes).
A set of decision rules is complete if it is able to cover all objects from the decision table in such a way that consistent objects are re-classified to their original classes and inconsistent objects are classified to clusters of classes referring to this inconsistency. We call minimal each set of decision rules that is complete and non-redundant, i.e. exclusion of any rule from this set makes it non-complete.
One of three induction strategies can be adopted to obtain a set of decision rules :
The most popular rule induction algorithm for dominance-based rough set approach is DOMLEM , which generates minimal set of rules.
Each object (student) is described by three criteria , related to the levels in Mathematics, Physics and Literatire, respectively. According to the decision attribute, the students are divided into three preference-ordered classes:
, related to the levels in Mathematics, Physics and Literatire, respectively. According to the decision attribute, the students are divided into three preference-ordered classes: 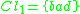 ,
,  and
and 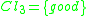 . Thus, the following unions of classes were approximated:
. Thus, the following unions of classes were approximated:
Notice that evaluations of objects and
and 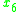 are inconsistent, because
are inconsistent, because  has better evaluations on all three criteria than
has better evaluations on all three criteria than 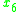 but worse global score.
but worse global score.
Therefore, lower approximations of class unions consist of the following objects:
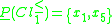
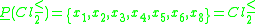

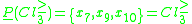
Thus, only classes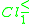 and
and  cannot be approximated precisely. Their upper approximations are as follows:
cannot be approximated precisely. Their upper approximations are as follows:
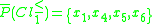
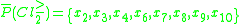
while their boundary regions are:

Of course, since and
and 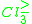 are approximated precisely, we have
are approximated precisely, we have 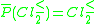 ,
, 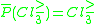 and
and 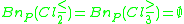
The following minimal set of 10 rules can be induced from the decision table:
The last rule is approximate, while the rest are certain.
, multicriteria choice and ranking
problems, can also be solved using dominance-based rough set approach. This is done by converting the decision table into pairwise comparison table (PCT).
stochastic case. The method is based on estimating the conditional probabilities using the nonparametric maximum likelihood
method which leads
to the problem of isotonic regression.
Stochastic dominance-based rough sets can also be regarded as a sort of variable-consistency model.
for multiple criteria classification problems based on dominance-based rough sets (DRSA). JAMM is a much more advanced successor of 4eMka2. Both systems are freely available for non-profit purposes on the Laboratory of Intelligent Decision Support Systems (IDSS) website.
Rough set
In computer science, a rough set, first described by a Polish computer scientist Zdzisław I. Pawlak, is a formal approximation of a crisp set in terms of a pair of sets which give the lower and the upper approximation of the original set...
for multi-criteria decision analysis
Multi-Criteria Decision Analysis
Multiple-criteria decision-making or multiple-criteria decision analysis is a sub-discipline of operations research that explicitly considers multiple criteria in decision-making environments. Whether in our daily lives or in professional settings, there are typically multiple conflicting criteria...
(MCDA), introduced by Greco, Matarazzo and Słowiński. The main change comparing to the classical rough sets is the substitution of the indiscernibility relation by a dominance relation, which permits to deal with inconsistencies typical to consideration of criteria and preference-ordered decision classes.
Multicriteria classification (sorting)
Multicriteria classificationMulticriteria classification
In multiple criteria decision aiding , multicriteria classification involves problems where a finite set of alternative actions should be assigned into a predefined set of preferentially ordered categories...
(sorting) is one of the problems considered within MCDA and can be stated as follows: given a set of objects evaluated by a set of criteria (attributes with preference-order domains), assign these objects to some pre-defined and preference-ordered decision classes, such that each object is assigned to exactly one class. Due to the preference ordering, improvement of evaluations of an object on the criteria should not worsen its class assignment. The sorting problem is very similar to the problem of classification, however, in the latter, the objects are evaluated by regular attributes and the decision classes are not necessarily preference ordered. The problem of multicriteria classification is also referred to as ordinal classification problem with monotonicity constraints and often appears in real-life application when ordinal
Ordinal
Ordinal may refer to:* Ordinal number , a word representing the rank of a number* Ordinal scale, ranking things that are not necessarily numbers* Ordinal indicator, the sign adjacent to a numeral denoting that it is an ordinal number...
and monotone
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
properties follow from the domain knowledge about the problem.
As an illustrative example, consider the problem of evaluation in a high school. The director of the school wants to assign students (objects) to three classes: bad, medium and good (notice that class good is preferred to medium and medium is preferred to bad). Each student is described by three criteria: level in Physics, Mathematics and Literature, each taking one of three possible values bad, medium and good. Criteria are preference-ordered and improving the level from one of the subjects should not result in worse global evaluation (class).
As a more serious example, consider classification of bank clients, from the viewpoint of bankruptcy risk, into classes safe and risky. This may involve such characteristics as "return on equity
Return on equity
Return on equity measures the rate of return on the ownership interest of the common stock owners. It measures a firm's efficiency at generating profits from every unit of shareholders' equity . ROE shows how well a company uses investment funds to generate earnings growth...
(ROE)", "return on investment
Return on investment
Return on investment is one way of considering profits in relation to capital invested. Return on assets , return on net assets , return on capital and return on invested capital are similar measures with variations on how “investment” is defined.Marketing not only influences net profits but also...
(ROI)" and "return on sales (ROS)". The domains of these attributes are not simply ordered but involve a preference order since, from the viewpoint of bank managers, greater values of ROE, ROI or ROS are better for clients being analysed for bankruptcy risk . Thus, these attributes are criteria. Neglecting this information in knowledge discovery
Knowledge discovery
Knowledge discovery is a concept of the field of computer science that describes the process of automatically searching large volumes of data for patterns that can be considered knowledge about the data . It is often described as deriving knowledge from the input data...
may lead to wrong conclusions.
Decision table
In DRSA, data are often presented using a particular form of decision tableDecision table
Decision tables are a precise yet compact way to model complicated logic.Decision tables, like flowcharts and if-then-else and switch-case statements, associate conditions with actions to perform, but in many cases do so in a more elegant way....
. Formally, a DRSA decision table is a 4-tuple
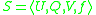 , where
, where 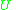 is a finite set of objects,
is a finite set of objects, 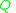 is a finite set of criteria,
is a finite set of criteria, 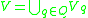 where
where  is the domain of the criterion
is the domain of the criterion 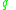 and
and 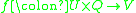 is an information function such that
is an information function such that 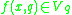 for every
for every 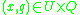 . The set
. The set 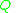 is divided into condition criteria (set
is divided into condition criteria (set 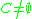 ) and the decision criterion (class)
) and the decision criterion (class) 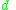 . Notice, that
. Notice, that 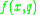 is an evaluation of object
is an evaluation of object 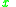 on criterion
on criterion 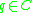 , while
, while 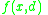 is the class assignment (decision value) of the object. An example of decision table is shown in Table 1 below.
is the class assignment (decision value) of the object. An example of decision table is shown in Table 1 below.Outranking relation
It is assumed that the domain of a criterion is completely preorder
is completely preorderPreorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
ed by an outranking relation
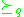 ;
; 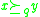 means that
means that  is at least as good as (outranks)
is at least as good as (outranks) 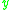 with respect to the criterion
with respect to the criterion 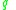 . Without loss of generality, we assume that the domain of
. Without loss of generality, we assume that the domain of 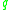 is a subset of reals
is a subset of realsReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
,
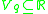 , and that the outranking relation is a simple order between real numbers
, and that the outranking relation is a simple order between real numbers 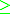 such that the following relation holds:
such that the following relation holds: 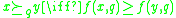 . This relation is straightforward for gain-type ("the more, the better") criterion, e.g. company profit. For cost-type ("the less, the better") criterion, e.g. product price, this relation can be satisfied by negating the values from
. This relation is straightforward for gain-type ("the more, the better") criterion, e.g. company profit. For cost-type ("the less, the better") criterion, e.g. product price, this relation can be satisfied by negating the values from 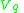 .
.Decision classes and class unions
Let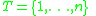 . The domain of decision criterion,
. The domain of decision criterion, 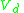 consist of
consist of 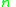 elements (without loss of generality we assume
elements (without loss of generality we assume  ) and induces a partition of
) and induces a partition of 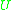 into
into 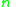 classes
classes 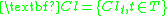 , where
, where 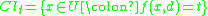 . Each object
. Each object 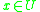 is assigned to one and only one class
is assigned to one and only one class  . The classes are preference-ordered according to an increasing order of class indices, i.e. for all
. The classes are preference-ordered according to an increasing order of class indices, i.e. for all 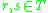 such that
such that 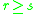 , the objects from
, the objects from 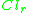 are strictly preferred to the objects from
are strictly preferred to the objects from 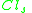 . For this reason, we can consider the upward and downward unions of classes, defined respectively, as:
. For this reason, we can consider the upward and downward unions of classes, defined respectively, as: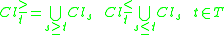
Dominance
We say that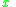 dominates
dominates 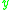 with respect to
with respect to  , denoted by
, denoted by 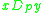 , if
, if  is better than
is better than  on every criterion from
on every criterion from  ,
, 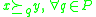 . For each
. For each 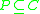 , the dominance relation
, the dominance relation 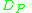 is reflexive
is reflexiveReflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
and transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
, i.e. it is a partial pre-order
Preorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
. Given
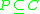 and
and 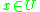 , let
, let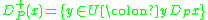
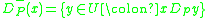
represent P-dominating set and P-dominated set with respect to
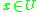 , respectively.
, respectively.Rough approximations
The key idea of the rough setRough set
In computer science, a rough set, first described by a Polish computer scientist Zdzisław I. Pawlak, is a formal approximation of a crisp set in terms of a pair of sets which give the lower and the upper approximation of the original set...
philosophy is approximation of one knowledge by another knowledge. In DRSA, the knowledge being approximated is a collection of upward and downward unions of decision classes and the "granules of knowledge" used for approximation are P-dominating and P-dominated sets.
The P-lower and the P-upper approximation of
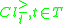 with respect to
with respect to 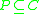 , denoted as
, denoted as 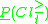 and
and  , respectively, are defined as:
, respectively, are defined as: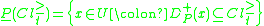
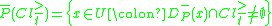
Analogously, the P-lower and the P-upper approximation of
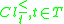 with respect to
with respect to 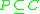 , denoted as
, denoted as 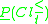 and
and 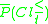 , respectively, are defined as:
, respectively, are defined as:
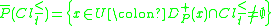
Lower approximations group the objects which certainly belong to class union
 (respectively
(respectively 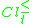 ). This certainty comes from the fact, that object
). This certainty comes from the fact, that object 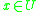 belongs to the lower approximation
belongs to the lower approximation 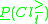 (respectively
(respectively 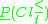 ), if no other object in
), if no other object in 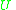 contradicts this claim, i.e. every object
contradicts this claim, i.e. every object 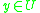 which P-dominates
which P-dominates 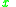 , also belong to the class union
, also belong to the class union  (respectively
(respectively 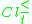 ). Upper approximations group the objects which could belong to
). Upper approximations group the objects which could belong to 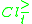 (respectively
(respectively 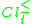 ), since object
), since object 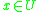 belongs to the upper approximation
belongs to the upper approximation 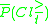 (respectively
(respectively  ), if there exist another object
), if there exist another object 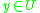 P-dominated by
P-dominated by 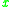 from class union
from class union  (respectively
(respectively  ).
).The P-lower and P-upper approximations defined as above satisfy the following properties for all
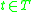 and for any
and for any  :
: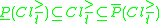
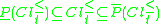
The P-boundaries (P-doubtful regions) of
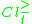 and
and 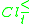 are defined as:
are defined as: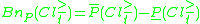

Quality of approximation and reducts
The ratio
defines the quality of approximation of the partition
 into classes by means of the set of criteria
into classes by means of the set of criteria 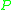 . This ratio express the relation between all the P-correctly classified objects and all the objects in the table.
. This ratio express the relation between all the P-correctly classified objects and all the objects in the table.Every minimal subset
 such that
such that 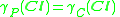 is called a reduct
is called a reductReduct
In universal algebra and in model theory, a reduct of an algebraic structure is obtained by omitting some of the operations and relations of that structure...
of
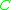 and is denoted by
and is denoted by  . A decision table may have more than one reduct. The intersection of all reducts is known as the core.
. A decision table may have more than one reduct. The intersection of all reducts is known as the core.Decision rules
On the basis of the approximations obtained by means of the dominance relations, it is possible to induce a generalized description of the preferential information contained in the decision table, in terms of decision rulesDecision rules
A set of decision rules is the verbal equivalent of a graphical decision tree, which specifies class membership based on a hierarchical sequence of decisions...
. The decision rules are expressions of the form if [condition] then [consequent], that represent a form of dependency between condition criteria and decision criteria. Procedures for generating decision rules from a decision table use an inducive learning principle. We can distinguish three types of rules: certain, possible and approximate. Certain rules are generated from lower approximations of unions of classes; possible rules are generated from upper approximations of unions of classes and approximate rules are generated from boundary regions.
Certain rules has the following form:
if
 and
and 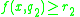 and
and 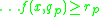 then
then 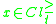
if
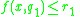 and
and 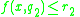 and
and 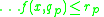 then
then 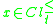
Possible rules has a similar syntax, however the consequent part of the rule has the form:
 could belong to
could belong to 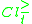 or the form:
or the form: 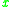 could belong to
could belong to 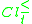 .
.Finally, approximate rules has the syntax:
if
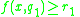 and
and 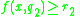 and
and 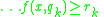 and
and 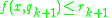 and
and 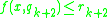 and
and 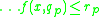
then
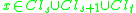
The certain, possible and approximate rules represent certain, possible and ambiguous knowledge extracted from the decision table.
Each decision rule should be minimal. Since a decision rule is an implication, by a minimal decision rule we understand such an implication that there is no other implication with an antecedent of at least the same weakness (in other words, rule using a subset of elementary conditions or/and weaker elementary conditions) and a consequent of at least the same strength (in other words, rule assigning objects to the same union or sub-union of classes).
A set of decision rules is complete if it is able to cover all objects from the decision table in such a way that consistent objects are re-classified to their original classes and inconsistent objects are classified to clusters of classes referring to this inconsistency. We call minimal each set of decision rules that is complete and non-redundant, i.e. exclusion of any rule from this set makes it non-complete.
One of three induction strategies can be adopted to obtain a set of decision rules :
- generation of a minimal description, i.e. a minimal set of rules,
- generation of an exhaustive description, i.e. all rules for a given data matrix,
- generation of a characteristic description, i.e. a set of rules covering relatively many objects each, however, all together not necessarily all objects from the decision table
The most popular rule induction algorithm for dominance-based rough set approach is DOMLEM , which generates minimal set of rules.
Example
Consider the following problem of high school students evaluations:| object (student) | 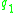 (Mathematics) | 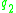 (Physics) | 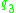 (Literature) | 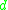 (global score) |
|
|---|---|---|---|---|---|
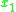 |
medium | medium | bad | bad | |
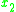 |
good | medium | bad | medium | |
 |
medium | good | bad | medium | |
 |
bad | medium | good | bad | |
 |
bad | bad | medium | bad | |
 |
bad | medium | medium | medium | |
 |
good | good | bad | good | |
 |
good | medium | medium | medium | |
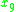 |
medium | medium | good | good | |
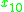 |
good | medium | good | good |
Each object (student) is described by three criteria
 , related to the levels in Mathematics, Physics and Literatire, respectively. According to the decision attribute, the students are divided into three preference-ordered classes:
, related to the levels in Mathematics, Physics and Literatire, respectively. According to the decision attribute, the students are divided into three preference-ordered classes: 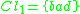 ,
,  and
and 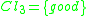 . Thus, the following unions of classes were approximated:
. Thus, the following unions of classes were approximated:-
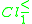 i.e. the class of (at most) bad students,
i.e. the class of (at most) bad students,
-
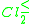 i.e. the class of at most medium students,
i.e. the class of at most medium students,
-
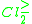 i.e. the class of at least medium students,
i.e. the class of at least medium students,
-
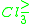 i.e. the class of (at least) good students.
i.e. the class of (at least) good students.
Notice that evaluations of objects
 and
and 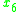 are inconsistent, because
are inconsistent, because  has better evaluations on all three criteria than
has better evaluations on all three criteria than 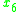 but worse global score.
but worse global score.Therefore, lower approximations of class unions consist of the following objects:
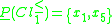
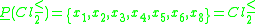

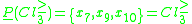
Thus, only classes
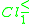 and
and  cannot be approximated precisely. Their upper approximations are as follows:
cannot be approximated precisely. Their upper approximations are as follows: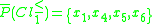
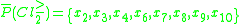
while their boundary regions are:

Of course, since
 and
and 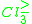 are approximated precisely, we have
are approximated precisely, we have 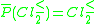 ,
, 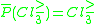 and
and 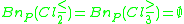
The following minimal set of 10 rules can be induced from the decision table:
- if
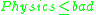 then
then 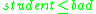
- if
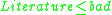 and
and 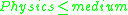 and
and 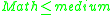 then
then 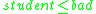
- if
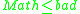 then
then 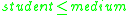
- if
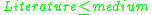 and
and 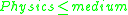 then
then 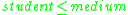
- if
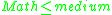 and
and 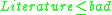 then
then 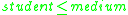
- if
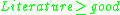 and
and 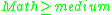 then
then 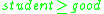
- if
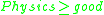 and
and 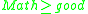 then
then 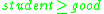
- if
 then
then 
- if
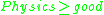 then
then 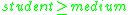
- if
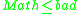 and
and  then
then 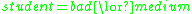
The last rule is approximate, while the rest are certain.
Multicriteria choice and ranking problems
The other two problems considered within multi-criteria decision analysisMulti-Criteria Decision Analysis
Multiple-criteria decision-making or multiple-criteria decision analysis is a sub-discipline of operations research that explicitly considers multiple criteria in decision-making environments. Whether in our daily lives or in professional settings, there are typically multiple conflicting criteria...
, multicriteria choice and ranking
Ranking
A ranking is a relationship between a set of items such that, for any two items, the first is either 'ranked higher than', 'ranked lower than' or 'ranked equal to' the second....
problems, can also be solved using dominance-based rough set approach. This is done by converting the decision table into pairwise comparison table (PCT).
Variable-consistency DRSA
The definitions of rough approximations are based on a strict application of the dominance principle. However, when defining non-ambiguous objects, it is reasonable to accept a limited proportion of negative examples, particularly for large decision tables. Such extended version of DRSA is called Variable-Consistency DRSA model (VC-DRSA)Stochastic DRSA
In real-life data, particularly for large datasets, the notions of rough approximations were found to be excessively restrictive. Therefore an extension of DRSA, based on stochastic model (Stochastic DRSA), which allows inconsistencies to some degree, has been introduced. Having stated the probabilistic model for ordinal classification problems with monotonicity constraints, the concepts of lower approximations are extended to thestochastic case. The method is based on estimating the conditional probabilities using the nonparametric maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
method which leads
to the problem of isotonic regression.
Stochastic dominance-based rough sets can also be regarded as a sort of variable-consistency model.
Software
4eMka2 is a decision support systemDecision support system
A decision support system is a computer-based information system that supports business or organizational decision-making activities. DSSs serve the management, operations, and planning levels of an organization and help to make decisions, which may be rapidly changing and not easily specified in...
for multiple criteria classification problems based on dominance-based rough sets (DRSA). JAMM is a much more advanced successor of 4eMka2. Both systems are freely available for non-profit purposes on the Laboratory of Intelligent Decision Support Systems (IDSS) website.
See also
- Rough sets
- Soft computingSoft computingSoft computing is a term applied to a field within computer science which is characterized by the use of inexact solutions to computationally-hard tasks such as the solution of NP-complete problems, for which an exact solution cannot be derived in polynomial time.-Introduction:Soft Computing became...
- Granular computingGranular computingGranular computing is an emerging computing paradigm of information processing. It concerns the processing of complex information entities called information granules, which arise in the process of data abstraction and derivation of knowledge from information...
- Multicriteria Decision Analysis (MCDA)
External links
- The International Rough Set Society
- Laboratory of Intelligent Decision Support Systems (IDSS) at Poznań University of Technology.
- Extensive list of DRSA references on the Roman Słowiński home page.

