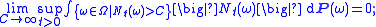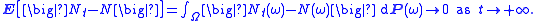Doob's martingale convergence theorems
Encyclopedia
In mathematics
— specifically, in stochastic analysis — Doob's martingale convergence theorems are a collection of results on the long-time limits
of supermartingale
s, named after the American
mathematician
Joseph Leo Doob
.
supermartingale with respect to the filtration F∗; in other words, for all 0 ≤ s ≤ t < +∞,
s Nt to have a limit as t → +∞ in a pointwise sense, i.e. for each ω in the sample space Ω individually.
For t ≥ 0, let Nt− = max(−Nt, 0) and suppose that
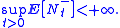
Then the pointwise limit
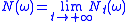
exists for P-almost all
ω ∈ Ω.
. In order to obtain convergence in L1 (i.e., convergence in mean
), one requires uniform integrability of the random variables Nt. By Chebyshev's inequality
, convergence in L1 implies convergence in probability and convergence in distribution.
The following are equivalent:
martingale such that
for some p > 1. Then there exists a random variable M ∈ Lp(Ω, P; R) such that Mt → M as t → +∞ both P-almost surely and in Lp(Ω, P; R).
Let M : N × Ω → R be a discrete-time martingale such that
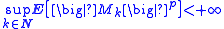
for some p > 1. Then there exists a random variable M ∈ Lp(Ω, P; R) such that Mk → M as k → +∞ both P-almost surely and in Lp(Ω, P; R)
s also have a convergence property.
Let (Ω, F, P) be a probability space
and let X be a random variable in L1. Let F∗ = (Fk)k∈N be any filtration
of F, and define F∞ to be the minimal σ-algebra generated by (Fk)k∈N. Then
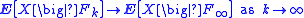
both P-almost surely and in L1.
This result is usually called Lévy's zero-one law. The reason for the name is that if A is an event in F∞, then the theorem says that
almost surely, i.e., the limit of the probabilities is 0 or 1. In plain language, if we are learning gradually all the information that determines the outcome of an event, then we will become gradually certain what the outcome will be. This sounds almost like a tautology
, but the result is still non-trivial. For instance, it easily implies Kolmogorov's zero-one law
, since it says that for any tail event A, we must have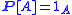
almost surely, hence 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
— specifically, in stochastic analysis — Doob's martingale convergence theorems are a collection of results on the long-time limits
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
of supermartingale
Martingale (probability theory)
In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
s, named after the American
United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Joseph Leo Doob
Joseph Leo Doob
Joseph Leo Doob was an American mathematician, specializing in analysis and probability theory.The theory of martingales was developed by Doob.-Early life and education:...
.
Statement of the theorems
In the following, (Ω, F, F∗, P), F∗ = (Ft)t≥0, will be a filtered probability space and N : [0, +∞) × Ω → R will be a right-continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
supermartingale with respect to the filtration F∗; in other words, for all 0 ≤ s ≤ t < +∞,
Doob's first martingale convergence theorem
Doob's first martingale convergence theorem provides a sufficient condition for the random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s Nt to have a limit as t → +∞ in a pointwise sense, i.e. for each ω in the sample space Ω individually.
For t ≥ 0, let Nt− = max(−Nt, 0) and suppose that
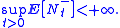
Then the pointwise limit
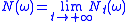
exists for P-almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
ω ∈ Ω.
Doob's second martingale convergence theorem
It is important to note that the convergence in Doob's first martingale convergence theorem is pointwise, not uniform, and is unrelated to convergence in mean square, or indeed in any Lp spaceLp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
. In order to obtain convergence in L1 (i.e., convergence in mean
Convergence of random variables
In probability theory, there exist several different notions of convergence of random variables. The convergence of sequences of random variables to some limit random variable is an important concept in probability theory, and its applications to statistics and stochastic processes...
), one requires uniform integrability of the random variables Nt. By Chebyshev's inequality
Chebyshev's inequality
In probability theory, Chebyshev’s inequality guarantees that in any data sample or probability distribution,"nearly all" values are close to the mean — the precise statement being that no more than 1/k2 of the distribution’s values can be more than k standard deviations away from the mean...
, convergence in L1 implies convergence in probability and convergence in distribution.
The following are equivalent:
- (Nt)t>0 is uniformly integrable, i.e.
- there exists an integrable random variable N ∈ L1(Ω, P; R) such that Nt → N as t → +∞ both P-almost surelyAlmost surelyIn probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
and in L1(Ω, P; R), i.e.
Corollary: convergence theorem for continuous martingales
Let M : [0, +∞) × Ω → R be a continuousSample continuous process
In mathematics, a sample-continuous process is a stochastic process whose sample paths are almost surely continuous functions.-Definition:Let be a probability space. Let X : I × Ω → S be a stochastic process, where the index set I and state space S...
martingale such that
for some p > 1. Then there exists a random variable M ∈ Lp(Ω, P; R) such that Mt → M as t → +∞ both P-almost surely and in Lp(Ω, P; R).
Discrete-time results
Similar results can be obtained for discrete-time supermartingales and submartingales, the obvious difference being that no continuity assumptions are required. For example, the result above becomesLet M : N × Ω → R be a discrete-time martingale such that
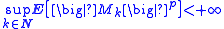
for some p > 1. Then there exists a random variable M ∈ Lp(Ω, P; R) such that Mk → M as k → +∞ both P-almost surely and in Lp(Ω, P; R)
Convergence of conditional expectations: Lévy's zero-one law
Doob's martingale convergence theorems imply that conditional expectationConditional expectation
In probability theory, a conditional expectation is the expected value of a real random variable with respect to a conditional probability distribution....
s also have a convergence property.
Let (Ω, F, P) be a probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
and let X be a random variable in L1. Let F∗ = (Fk)k∈N be any filtration
Filtration (abstract algebra)
In mathematics, a filtration is an indexed set Si of subobjects of a given algebraic structure S, with the index i running over some index set I that is a totally ordered set, subject to the condition that if i ≤ j in I then Si ⊆ Sj...
of F, and define F∞ to be the minimal σ-algebra generated by (Fk)k∈N. Then
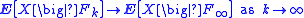
both P-almost surely and in L1.
This result is usually called Lévy's zero-one law. The reason for the name is that if A is an event in F∞, then the theorem says that
almost surely, i.e., the limit of the probabilities is 0 or 1. In plain language, if we are learning gradually all the information that determines the outcome of an event, then we will become gradually certain what the outcome will be. This sounds almost like a tautologyTautology
Tautology may refer to:*Tautology , using different words to say the same thing even if the repetition does not provide clarity. Tautology also means a series of self-reinforcing statements that cannot be disproved because the statements depend on the assumption that they are already...
, but the result is still non-trivial. For instance, it easily implies Kolmogorov's zero-one law
Kolmogorov's zero-one law
In probability theory, Kolmogorov's zero-one law, named in honor of Andrey Nikolaevich Kolmogorov, specifies that a certain type of event, called a tail event, will either almost surely happen or almost surely not happen; that is, the probability of such an event occurring is zero or one.Tail...
, since it says that for any tail event A, we must have
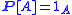almost surely, hence .