Dual cone and polar cone are closely related concepts in convex analysis

Convex analysis

Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory....

, a branch of mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

.

Dual cone

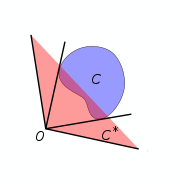
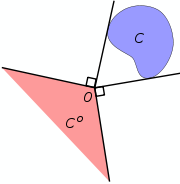
The dual cone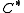 of a subset

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

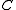  in a Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

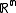  is the set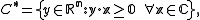


where "·" denotes the dot product

Dot product

In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...

.

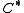is always a convex cone

Convex cone

In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...

, even if 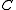is neither convex

Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

 nor a cone.

When 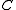is a cone, the following properties hold:

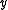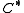• A non-zero vector is in if and only if is the normal
  Surface normal
  A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
  
   of a hyperplane
  Hyperplane
  A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
  
   that supports
  Supporting hyperplane
  Supporting hyperplane is a concept in geometry. A hyperplane divides a space into two half-spaces. A hyperplane is said to support a set S in Euclidean space \mathbb R^n if it meets both of the following:...
  
    at the origin.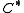
• is closed
  Closed set
  In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
  
   and convex.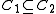
• implies .
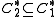• If 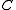has nonempty interior, then is pointed, i.e. contains no line in its entirety.
• If is a cone and the closure of 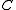is pointed, then 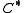has nonempty interior.
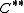• is the closure of the smallest convex cone containing .

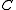A cone is said to be self-dual if 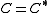. The nonnegative orthant

Orthant

In geometry, an orthant or hyperoctant is the analogue in n-dimensional Euclidean space of a quadrant in the plane or an octant in three dimensions....

 of 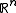and the space of all positive semidefinite matrices are self-dual.

Dual cones can be more generally defined on real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

 Hilbert space

Hilbert space

The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...

s.

Polar cone

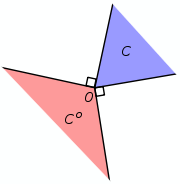
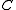For a set in 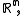the polar cone of 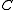is the set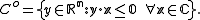


It is easy to check that 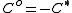for any set 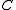in 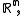and that the polar cone shares many of the properties of the dual cone.