
Dual wavelet
Encyclopedia
In mathematics
, a dual wavelet is the dual
to a wavelet
. In general, the wavelet series
generated by a square integrable function
will have a dual series, in the sense of the Riesz representation theorem
. However, the dual series is not in general representable by a square integral function itself.
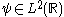 , define the series
, define the series 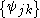 by
by

for integers .
.
Such a function is called an R-function if the linear span of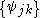 is dense
is dense
in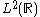 , and if there exist positive constants A, B with
, and if there exist positive constants A, B with 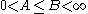 such that
such that
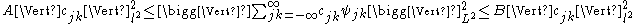
for all bi-infinite square summable series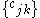 . Here,
. Here,  denotes the square-sum norm:
denotes the square-sum norm:
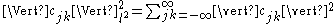
and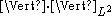 denotes the usual norm on
denotes the usual norm on 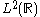 :
:
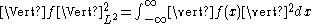
By the Riesz representation theorem
, there exists a unique dual basis such that
such that
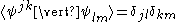
where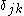 is the Kronecker delta and
is the Kronecker delta and  is the usual inner product on
is the usual inner product on 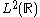 . Indeed, there exists a unique series representation for a square integrable function f expressed in this basis:
. Indeed, there exists a unique series representation for a square integrable function f expressed in this basis:
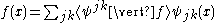
If there exists a function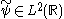 such that
such that
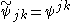
then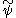 is called the dual wavelet or the wavelet dual to ψ. In general, for some given R-function ψ, the dual will not exist. In the special case of
is called the dual wavelet or the wavelet dual to ψ. In general, for some given R-function ψ, the dual will not exist. In the special case of 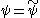 , the wavelet is said to be an orthogonal wavelet
, the wavelet is said to be an orthogonal wavelet
.
An example of an R-function without a dual is easy to construct. Let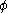 be an orthogonal wavelet. Then define
be an orthogonal wavelet. Then define 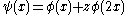 for some complex number z. It is straightforward to show that this ψ does not have a wavelet dual.
for some complex number z. It is straightforward to show that this ψ does not have a wavelet dual.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a dual wavelet is the dual
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
to a wavelet
Wavelet
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
. In general, the wavelet series
Wavelet series
In mathematics, a wavelet series is a representation of a square-integrable function by a certain orthonormal series generated by a wavelet...
generated by a square integrable function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
will have a dual series, in the sense of the Riesz representation theorem
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
. However, the dual series is not in general representable by a square integral function itself.
Definition
Given a square integrable function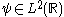 , define the series
, define the series 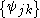 by
by
for integers
 .
.Such a function is called an R-function if the linear span of
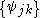 is dense
is denseDense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
in
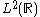 , and if there exist positive constants A, B with
, and if there exist positive constants A, B with 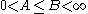 such that
such that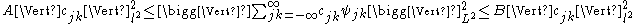
for all bi-infinite square summable series
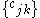 . Here,
. Here,  denotes the square-sum norm:
denotes the square-sum norm: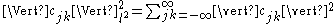
and
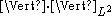 denotes the usual norm on
denotes the usual norm on 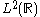 :
: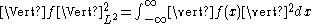
By the Riesz representation theorem
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
, there exists a unique dual basis
 such that
such that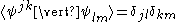
where
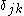 is the Kronecker delta and
is the Kronecker delta and  is the usual inner product on
is the usual inner product on 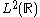 . Indeed, there exists a unique series representation for a square integrable function f expressed in this basis:
. Indeed, there exists a unique series representation for a square integrable function f expressed in this basis: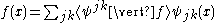
If there exists a function
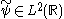 such that
such that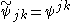
then
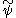 is called the dual wavelet or the wavelet dual to ψ. In general, for some given R-function ψ, the dual will not exist. In the special case of
is called the dual wavelet or the wavelet dual to ψ. In general, for some given R-function ψ, the dual will not exist. In the special case of 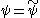 , the wavelet is said to be an orthogonal wavelet
, the wavelet is said to be an orthogonal waveletOrthogonal wavelet
An orthogonal wavelet is a wavelet where the associated wavelet transform is orthogonal.That is the inverse wavelet transform is the adjoint of the wavelet transform.If this condition is weakened you may end up with biorthogonal wavelets.- Basics :...
.
An example of an R-function without a dual is easy to construct. Let
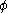 be an orthogonal wavelet. Then define
be an orthogonal wavelet. Then define 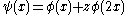 for some complex number z. It is straightforward to show that this ψ does not have a wavelet dual.
for some complex number z. It is straightforward to show that this ψ does not have a wavelet dual.

