
Wavelet series
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a wavelet series is a representation of a square-integrable (real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
- or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
-valued) function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
by a certain orthonormal series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
generated by a wavelet
Wavelet
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
. This article provides a formal, mathematical definition of an orthonormal wavelet and of the integral wavelet transform.
Formal definition
A function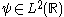 is called an orthonormal wavelet if it can be used to define a Hilbert basis, that is a complete
is called an orthonormal wavelet if it can be used to define a Hilbert basis, that is a completeComplete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
orthonormal system
Orthonormality
In linear algebra, two vectors in an inner product space are orthonormal if they are orthogonal and both of unit length. A set of vectors form an orthonormal set if all vectors in the set are mutually orthogonal and all of unit length...
, for the Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
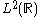 of square integrable
of square integrableLp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
functions. The Hilbert basis is constructed as the family of functions
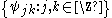 by means of dyadic
by means of dyadicDyadic transformation
The dyadic transformation is the mapping produced by the rule...
translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
s and dilations of
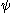 ,
,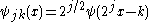
for integers
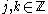 . This family is an orthonormal system if it is orthonormal under the inner product
. This family is an orthonormal system if it is orthonormal under the inner product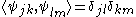
where
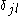 is the Kronecker delta and
is the Kronecker delta and 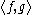 is the standard inner product
is the standard inner product 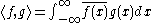 on
on 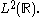
The requirement of completeness is that every function
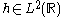 may be expanded in the basis as
may be expanded in the basis as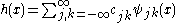
with convergence of the series understood to be convergence in norm. Such a representation of a function f is known as a wavelet series. This implies that an orthonormal wavelet is self-dual
Dual wavelet
In mathematics, a dual wavelet is the dual to a wavelet. In general, the wavelet series generated by a square integrable function will have a dual series, in the sense of the Riesz representation theorem...
.
Wavelet transform
The integral wavelet transform is the integral transform defined as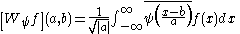
The wavelet coefficients
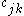 are then given by
are then given by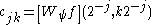
Here,
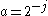 is called the binary dilation or dyadic dilation, and
is called the binary dilation or dyadic dilation, and 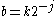 is the binary or dyadic position.
is the binary or dyadic position.Wavelet compression
Wavelet compression is a form of data compressionData compression
In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
well suited for image compression
Image compression
The objective of image compression is to reduce irrelevance and redundancy of the image data in order to be able to store or transmit data in an efficient form.- Lossy and lossless compression :...
(sometimes also video compression and audio compression). Notable implementations are JPEG 2000
JPEG 2000
JPEG 2000 is an image compression standard and coding system. It was created by the Joint Photographic Experts Group committee in 2000 with the intention of superseding their original discrete cosine transform-based JPEG standard with a newly designed, wavelet-based method...
and ECW
ECW (file format)
ECW is a proprietary wavelet compression image format optimized for aerial and satellite imagery. It was developed by Earth Resource Mapping, and is now owned by ERDAS, which is owned by Intergraph...
for still images, and REDCODE
REDCODE
REDCODE RAW is a proprietary multimedia audio/video file format owned by Red Digital Cinema Camera Company and featuring lossy compression for video contents and lossless for audio contents...
, the BBC's Dirac
Dirac (codec)
Dirac is an open and royalty-free video compression format, specification and system developed by BBC Research at the BBC. Schrödinger and dirac-research are open and royalty-free software implementations of Dirac...
, and Ogg Tarkin for video. The goal is to store image data in as little space as possible in a file
Computer file
A computer file is a block of arbitrary information, or resource for storing information, which is available to a computer program and is usually based on some kind of durable storage. A file is durable in the sense that it remains available for programs to use after the current program has finished...
. Wavelet compression can be either lossless
Lossless data compression
Lossless data compression is a class of data compression algorithms that allows the exact original data to be reconstructed from the compressed data. The term lossless is in contrast to lossy data compression, which only allows an approximation of the original data to be reconstructed, in exchange...
or lossy
Lossy data compression
In information technology, "lossy" compression is a data encoding method that compresses data by discarding some of it. The procedure aims to minimize the amount of data that need to be held, handled, and/or transmitted by a computer...
.
Using a wavelet transform, the wavelet compression methods are adequate for representing transients, such as percussion sounds in audio, or high-frequency components in two-dimensional images, for example an image of stars on a night sky. This means that the transient elements of a data signal can be represented by a smaller amount of information than would be the case if some other transform, such as the more widespread discrete cosine transform
Discrete cosine transform
A discrete cosine transform expresses a sequence of finitely many data points in terms of a sum of cosine functions oscillating at different frequencies. DCTs are important to numerous applications in science and engineering, from lossy compression of audio and images A discrete cosine transform...
, had been used.
Wavelet compression is not good for all kinds of data: transient signal characteristics mean good wavelet compression, while smooth, periodic signals are better compressed by other methods, particularly traditional harmonic compression (frequency domain, as by Fourier transforms and related). Data statistically indistinguishable from random noise is not compressible by any means.
See Diary Of An x264 Developer: The problems with wavelets (2010) for discussion of practical issues of current methods using wavelets for video compression.
Method
First a wavelet transform is applied.This produces as many coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s as there are pixel
Pixel
In digital imaging, a pixel, or pel, is a single point in a raster image, or the smallest addressable screen element in a display device; it is the smallest unit of picture that can be represented or controlled....
s in the image (i.e.: there is no compression yet since it is only a transform).
These coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s can then be compressed more easily because the information is statistically concentrated in just a few coefficients.
This principle is called transform coding
Transform coding
Transform coding is a type of data compression for "natural" data like audio signals or photographic images. The transformation is typically lossy, resulting in a lower quality copy of the original input....
.
After that, the coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s are quantized
Quantization (signal processing)
Quantization, in mathematics and digital signal processing, is the process of mapping a large set of input values to a smaller set – such as rounding values to some unit of precision. A device or algorithmic function that performs quantization is called a quantizer. The error introduced by...
and the quantized values are entropy encoded
Entropy encoding
In information theory an entropy encoding is a lossless data compression scheme that is independent of the specific characteristics of the medium....
and/or run length encoded
Run-length encoding
Run-length encoding is a very simple form of data compression in which runs of data are stored as a single data value and count, rather than as the original run...
.
A few 1D and 2D applications of wavelet compression use a technique called "wavelet footprints".
Other Practical Applications
The wavelet transform can provide us with the frequency of the signals and the time associated to those frequencies, making it very convenient for its application in numerous fields. For instance, signal processing of accelerations for gait analysis.See also
- Continuous wavelet transformContinuous wavelet transformA continuous wavelet transform is used to divide a continuous-time function into wavelets. Unlike Fourier transform, the continuous wavelet transform possesses the ability to construct a time-frequency representation of a signal that offers very good time and frequency localization...
- Discrete wavelet transformDiscrete wavelet transformIn numerical analysis and functional analysis, a discrete wavelet transform is any wavelet transform for which the wavelets are discretely sampled...
- Complex wavelet transformComplex wavelet transformThe complex wavelet transform is a complex-valued extension to the standard discrete wavelet transform . It is a two-dimensional wavelet transform which provides multiresolution, sparse representation, and useful characterization of the structure of an image. Further, it purveys a high degree of...
- Dual waveletDual waveletIn mathematics, a dual wavelet is the dual to a wavelet. In general, the wavelet series generated by a square integrable function will have a dual series, in the sense of the Riesz representation theorem...
- Multiresolution analysisMultiresolution analysisA multiresolution analysis or multiscale approximation is the design method of most of the practically relevant discrete wavelet transforms and the justification for the algorithm of the fast wavelet transform...
- ECWECW (file format)ECW is a proprietary wavelet compression image format optimized for aerial and satellite imagery. It was developed by Earth Resource Mapping, and is now owned by ERDAS, which is owned by Intergraph...
, a wavelet-based geospatialGeospatialGeospatial analysis is an approach to applying statistical analysis and other informational techniques to geographically based data. Such analysis employs spatial software and analytical methods with terrestrial or geographic datasets, including geographic information systems and...
image format designed for speed and processing efficiency - JPEG 2000JPEG 2000JPEG 2000 is an image compression standard and coding system. It was created by the Joint Photographic Experts Group committee in 2000 with the intention of superseding their original discrete cosine transform-based JPEG standard with a newly designed, wavelet-based method...
, a wavelet-based image compressionImage compressionThe objective of image compression is to reduce irrelevance and redundancy of the image data in order to be able to store or transmit data in an efficient form.- Lossy and lossless compression :...
standard - Some people generate spectrogramSpectrogramA spectrogram is a time-varying spectral representation that shows how the spectral density of a signal varies with time. Also known as spectral waterfalls, sonograms, voiceprints, or voicegrams, spectrograms are used to identify phonetic sounds, to analyse the cries of animals; they were also...
s using wavelets, called scaleogramScaleogramIn signal processing, a scaleogram or scalogram is a visual method of displaying a wavelet transform. There are 3 axes: x representing time, y representing scale, and z representing coefficient value. The z axis is often shown by varying the colour or brightness.A scaleogram is the equivalent of...
s. Other people generate spectrograms using a short-time Fourier transformShort-time Fourier transformThe short-time Fourier transform , or alternatively short-term Fourier transform, is a Fourier-related transform used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time.... - Chirplet transformChirplet transformIn signal processing, the chirplet transform is an inner product of an input signal with a family of analysis primitives called chirplets.-Similarity to other transforms:...
- Time-frequency representationTime-frequency representationA time–frequency representation is a view of a signal represented over both time and frequency. Time–frequency analysis means analysis into the time–frequency domain provided by a TFR...

