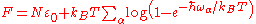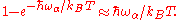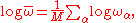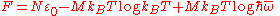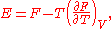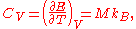Dulong–Petit law
Encyclopedia
The Dulong–Petit law, a chemical law
proposed in 1819 by French physicists Pierre Louis Dulong
and Alexis Thérèse Petit
, states the classical expression for the molar specific heat capacity of a crystal
. Experimentally the two scientists had found that the heat capacity per weight (the mass-specific heat capacity) for a number of substances became close to a constant value, after it had been multiplied by number-ratio representing the presumed relative atomic weight of the substance. These atomic weight
s had shortly before been suggested by Dalton
.
In modern terms, Dulong and Petit found that the heat capacity of a mole
of many solid substances is about 3R, where R is the modern constant called the universal gas constant
. Dulong and Petit were unaware of the relationship with R, since this constant had not yet been defined from the later kinetic theory
of gasses. The value of 3R is about 25 joule
s per Kelvin
.
The modern theory of the heat capacity of solids states that it is due to lattice vibration
s in the solid, and was first derived in crude form from this assumption by Albert Einstein
, in 1907. The Einstein solid
model thus gave for the first time a reason why the Dulong–Petit law should be stated in terms of the classical heat capacities for gases.
(measured in joule per kelvin per mole) and M is the molar mass
(measured in kilogram per mole). Thus, the heat capacity per mole of many solids is 3R.
Thus, in modern form the Dulong–Petit law is:
c M = 3R or c = 3R/M
Dulong and Petit did not state their law in terms of the gas constant
R (which was not then known). Instead, they measured the values of heat capacities (per weight) of substances and found them smaller for substances of greater "atomic weight" as inferred by Dalton. Dulong and Petit then found that when multiplied by these atomic weights, the value for the heat capacity (which would now be the heat capacity per mole
in modern terms) was nearly constant, and equal to a value which was later recognized to be 3 R.
In other modern terminology, the dimensionless heat capacity is equal to 3.
s. This is because in the classical theory of heat capacity
the heat capacity of solids approaches a maximum of 3R per mole
of atoms, due to the fact that full vibrational-mode degrees of freedom amount to 3 degrees of freedom per atom each corresponding to a quadratic kinetic energy term and a quadratic potential energy term. By the equipartition theorem, the average of each quadratic term is 1/2 kT, or 1/2 RT per mole (see derivation below). Multiplied by 3 degrees of freedom and the two terms per degree of freedom, this amounts to 3R per mole heat capacity.
The Dulong-Petit law fails at room temperatures for light atoms bonded strongly to each other, such as in metallic beryllium, and in carbon as diamond. Here, it predicts higher heat capacities than are actually found, with the difference due to higher-energy vibrational modes not being populated at room temperatures in these substances.
In the very low (cryogenic) temperature region, where the quantum mechanical nature of energy storage in all solids manifests itself with larger and larger effect, the law fails for all substances. For crystals under such conditions, the Debye model
, an extension of the Einstein theory that accounts for statistical distributions in atomic vibration when there are lower amounts of energy to distribute, works well.
of the system can be written as
where the index α sums over all the degrees of freedom. In the 1907 Einstein model
(as opposed to the later Debye model
) we consider only the high-energy limit:
Then
and we have
Define geometric mean frequency by
where M measures the total number of degrees of freedom of the system.
Thus we have
Using energy
we have
This gives specific heat
which is independent of the temperature.
article is translated)
Scientific law
A scientific law is a statement that explains what something does in science just like Newton's law of universal gravitation. A scientific law must always apply under the same conditions, and implies a causal relationship between its elements. The law must be confirmed and broadly agreed upon...
proposed in 1819 by French physicists Pierre Louis Dulong
Pierre Louis Dulong
Pierre Louis Dulong was a French physicist and chemist, remembered today largely for the law of Dulong and Petit. He worked on the specific heat capacity and the expansion and refractive indices of gases....
and Alexis Thérèse Petit
Alexis Thérèse Petit
Alexis Thérèse Petit was a French physicist. Petit is known for his work on the efficiencies of air- and steam-engines, published in 1818...
, states the classical expression for the molar specific heat capacity of a crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
. Experimentally the two scientists had found that the heat capacity per weight (the mass-specific heat capacity) for a number of substances became close to a constant value, after it had been multiplied by number-ratio representing the presumed relative atomic weight of the substance. These atomic weight
Atomic weight
Atomic weight is a dimensionless physical quantity, the ratio of the average mass of atoms of an element to 1/12 of the mass of an atom of carbon-12...
s had shortly before been suggested by Dalton
John Dalton
John Dalton FRS was an English chemist, meteorologist and physicist. He is best known for his pioneering work in the development of modern atomic theory, and his research into colour blindness .-Early life:John Dalton was born into a Quaker family at Eaglesfield, near Cockermouth, Cumberland,...
.
In modern terms, Dulong and Petit found that the heat capacity of a mole
Mole (unit)
The mole is a unit of measurement used in chemistry to express amounts of a chemical substance, defined as an amount of a substance that contains as many elementary entities as there are atoms in 12 grams of pure carbon-12 , the isotope of carbon with atomic weight 12. This corresponds to a value...
of many solid substances is about 3R, where R is the modern constant called the universal gas constant
Gas constant
The gas constant is a physical constant which is featured in many fundamental equations in the physical sciences, such as the ideal gas law and the Nernst equation. It is equivalent to the Boltzmann constant, but expressed in units of energy The gas constant (also known as the molar, universal,...
. Dulong and Petit were unaware of the relationship with R, since this constant had not yet been defined from the later kinetic theory
Kinetic theory
The kinetic theory of gases describes a gas as a large number of small particles , all of which are in constant, random motion. The rapidly moving particles constantly collide with each other and with the walls of the container...
of gasses. The value of 3R is about 25 joule
Joule
The joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...
s per Kelvin
Kelvin
The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
.
The modern theory of the heat capacity of solids states that it is due to lattice vibration
Phonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
s in the solid, and was first derived in crude form from this assumption by Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
, in 1907. The Einstein solid
Einstein solid
The Einstein solid is a model of a solid based on two assumptions:* Each atom in the lattice is an independent 3D quantum harmonic oscillator* All atoms oscillate with the same frequency...
model thus gave for the first time a reason why the Dulong–Petit law should be stated in terms of the classical heat capacities for gases.
Equivalent forms of statement of the law
An equivalent statement of the Dulong–Petit law in modern terms is that, regardless of the nature of the substance or crystal, the specific heat capacity c of a solid substance (measured in joule per kelvin per kilogram) is equal to 3R/M, where R is the gas constantGas constant
The gas constant is a physical constant which is featured in many fundamental equations in the physical sciences, such as the ideal gas law and the Nernst equation. It is equivalent to the Boltzmann constant, but expressed in units of energy The gas constant (also known as the molar, universal,...
(measured in joule per kelvin per mole) and M is the molar mass
Molar mass
Molar mass, symbol M, is a physical property of a given substance , namely its mass per amount of substance. The base SI unit for mass is the kilogram and that for amount of substance is the mole. Thus, the derived unit for molar mass is kg/mol...
(measured in kilogram per mole). Thus, the heat capacity per mole of many solids is 3R.
Thus, in modern form the Dulong–Petit law is:
c M = 3R or c = 3R/M
Dulong and Petit did not state their law in terms of the gas constant
Gas constant
The gas constant is a physical constant which is featured in many fundamental equations in the physical sciences, such as the ideal gas law and the Nernst equation. It is equivalent to the Boltzmann constant, but expressed in units of energy The gas constant (also known as the molar, universal,...
R (which was not then known). Instead, they measured the values of heat capacities (per weight) of substances and found them smaller for substances of greater "atomic weight" as inferred by Dalton. Dulong and Petit then found that when multiplied by these atomic weights, the value for the heat capacity (which would now be the heat capacity per mole
Mole (unit)
The mole is a unit of measurement used in chemistry to express amounts of a chemical substance, defined as an amount of a substance that contains as many elementary entities as there are atoms in 12 grams of pure carbon-12 , the isotope of carbon with atomic weight 12. This corresponds to a value...
in modern terms) was nearly constant, and equal to a value which was later recognized to be 3 R.
In other modern terminology, the dimensionless heat capacity is equal to 3.
Application limits
Despite its simplicity, Dulong–Petit law offers fairly good prediction for the specific heat capacity of many solids with relatively simple crystal structure at high temperatureTemperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
s. This is because in the classical theory of heat capacity
Heat capacity
Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...
the heat capacity of solids approaches a maximum of 3R per mole
Mole (unit)
The mole is a unit of measurement used in chemistry to express amounts of a chemical substance, defined as an amount of a substance that contains as many elementary entities as there are atoms in 12 grams of pure carbon-12 , the isotope of carbon with atomic weight 12. This corresponds to a value...
of atoms, due to the fact that full vibrational-mode degrees of freedom amount to 3 degrees of freedom per atom each corresponding to a quadratic kinetic energy term and a quadratic potential energy term. By the equipartition theorem, the average of each quadratic term is 1/2 kT, or 1/2 RT per mole (see derivation below). Multiplied by 3 degrees of freedom and the two terms per degree of freedom, this amounts to 3R per mole heat capacity.
The Dulong-Petit law fails at room temperatures for light atoms bonded strongly to each other, such as in metallic beryllium, and in carbon as diamond. Here, it predicts higher heat capacities than are actually found, with the difference due to higher-energy vibrational modes not being populated at room temperatures in these substances.
In the very low (cryogenic) temperature region, where the quantum mechanical nature of energy storage in all solids manifests itself with larger and larger effect, the law fails for all substances. For crystals under such conditions, the Debye model
Debye model
In thermodynamics and solid state physics, the Debye model is a method developed by Peter Debye in 1912 for estimating the phonon contribution to the specific heat in a solid. It treats the vibrations of the atomic lattice as phonons in a box, in contrast to the Einstein model, which treats the...
, an extension of the Einstein theory that accounts for statistical distributions in atomic vibration when there are lower amounts of energy to distribute, works well.
Derivation
A system of vibrations in a crystalline solid lattice can be modelled by considering harmonic oscillator potentials along each degree of freedom. Then, the free energyThermodynamic free energy
The thermodynamic free energy is the amount of work that a thermodynamic system can perform. The concept is useful in the thermodynamics of chemical or thermal processes in engineering and science. The free energy is the internal energy of a system less the amount of energy that cannot be used to...
of the system can be written as
where the index α sums over all the degrees of freedom. In the 1907 Einstein model
Einstein solid
The Einstein solid is a model of a solid based on two assumptions:* Each atom in the lattice is an independent 3D quantum harmonic oscillator* All atoms oscillate with the same frequency...
(as opposed to the later Debye model
Debye model
In thermodynamics and solid state physics, the Debye model is a method developed by Peter Debye in 1912 for estimating the phonon contribution to the specific heat in a solid. It treats the vibrations of the atomic lattice as phonons in a box, in contrast to the Einstein model, which treats the...
) we consider only the high-energy limit:
Then
and we have
Define geometric mean frequency by
where M measures the total number of degrees of freedom of the system.
Thus we have
Using energy
we have
This gives specific heat
which is independent of the temperature.
External links
(Annales de Chimie et de PhysiqueAnnales de chimie et de physique
Annales de chimie et de physique is a scientific journal that was founded in Paris, France, in 1789 under the title Annales de chimie. One of the early editors was the French chemist Antoine Lavoisier. In 1815, it became the Annales de chimie et de physique, and was published under that name for...
article is translated)