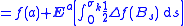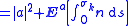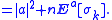Dynkin's formula
Encyclopedia
In mathematics
— specifically, in stochastic analysis — Dynkin's formula is a theorem giving the expected value
of any suitably smooth statistic of an Itō diffusion
at a stopping time. It may be seen as a stochastic generalization of the (second) fundamental theorem of calculus
. It is named after the Russia
n mathematician
Eugene Dynkin
.
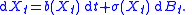
For a point x ∈ Rn, let Px denote the law of X given initial datum X0 = x, and let Ex denote expectation with respect to Px.
Let A be the infinitesimal generator
of X, defined by its action on compactly-supported C2 (twice differentiable with continuous second derivative) functions f : Rn → R as

or, equivalently,
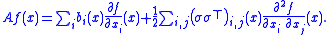
Let τ be a stopping time with Ex[τ] < +∞, and let f be C2 with compact support. Then Dynkin's formula holds:
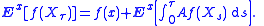
In fact, if τ is the first exit time for a bounded set
B ⊂ Rn with Ex[τ] < +∞, then Dynkin's formula holds for all C2 functions f, without the assumption of compact support.
B from the closed ball
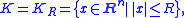
which, when B starts at a point a in the interior
of K, is given by
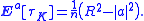
Choose an integer
k. The strategy is to apply Dynkin's formula with X = B, τ = σk = min(k, τK), and a compactly-supported C2 f with f(x) = |x|2 on K. The generator of Brownian motion is Δ/2, where Δ denotes the Laplacian operator. Therefore, by Dynkin's formula,
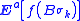
Hence, for any k,
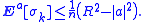
Now let k → +∞ to conclude that τK = limk→+∞σk < +∞ almost surely
and
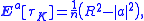
as claimed.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
— specifically, in stochastic analysis — Dynkin's formula is a theorem giving the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of any suitably smooth statistic of an Itō diffusion
Ito diffusion
In mathematics — specifically, in stochastic analysis — an Itō diffusion is a solution to a specific type of stochastic differential equation. That equation is similar to the Langevin equation, used in Physics to describe the brownian motion of a particle subjected to a potential in a...
at a stopping time. It may be seen as a stochastic generalization of the (second) fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
. It is named after the Russia
Russia
Russia or , officially known as both Russia and the Russian Federation , is a country in northern Eurasia. It is a federal semi-presidential republic, comprising 83 federal subjects...
n mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Eugene Dynkin
Eugene Dynkin
Eugene Borisovich Dynkin is a Soviet and American mathematician. He has made contributions to the fields of probability and algebra, especially semisimple Lie groups, Lie algebras, and Markov processes...
.
Statement of the theorem
Let X be the Rn-valued Itō diffusion solving the stochastic differential equationStochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
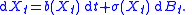
For a point x ∈ Rn, let Px denote the law of X given initial datum X0 = x, and let Ex denote expectation with respect to Px.
Let A be the infinitesimal generator
Infinitesimal generator (stochastic processes)
In mathematics — specifically, in stochastic analysis — the infinitesimal generator of a stochastic process is a partial differential operator that encodes a great deal of information about the process...
of X, defined by its action on compactly-supported C2 (twice differentiable with continuous second derivative) functions f : Rn → R as

or, equivalently,
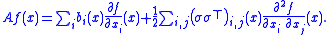
Let τ be a stopping time with Ex[τ] < +∞, and let f be C2 with compact support. Then Dynkin's formula holds:
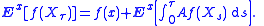
In fact, if τ is the first exit time for a bounded set
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
B ⊂ Rn with Ex[τ] < +∞, then Dynkin's formula holds for all C2 functions f, without the assumption of compact support.
Example
Dynkin's formula can be used to find the expected first exit time τK of Brownian motionBrownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
B from the closed ball
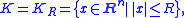
which, when B starts at a point a in the interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of K, is given by
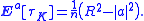
Choose an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
k. The strategy is to apply Dynkin's formula with X = B, τ = σk = min(k, τK), and a compactly-supported C2 f with f(x) = |x|2 on K. The generator of Brownian motion is Δ/2, where Δ denotes the Laplacian operator. Therefore, by Dynkin's formula,
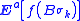
Hence, for any k,
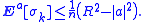
Now let k → +∞ to conclude that τK = limk→+∞σk < +∞ almost surely
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
and
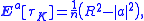
as claimed.