Dynkin system
Encyclopedia
A Dynkin system, named after Eugene Dynkin
, is a collection
of subset
s of another universal set
satisfying a set of axiom
s weaker than those of σ-algebra. Dynkin systems are sometimes referred to as λ-systems (Dynkin himself used this term) or d-system. These set families have applications in measure theory.
be a collection of subsets of Ω (i.e., 
is a subset of the power set of Ω). Then 
is a Dynkin system if
Equivalently,
is a Dynkin system if
An important fact is that a Dynkin system which is also a π-system
(i.e., closed under finite intersection) is a σ-algebra.
Given any collection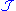
of subsets of 
, there exists a unique Dynkin system denoted 
which is minimal with respect to containing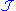 
. That is, if 
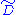is any Dynkin system containing 
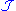, then 
. 
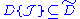is called the Dynkin system generated by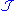 
. Note 
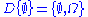. For another example, let 
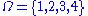and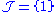 
; then 
.
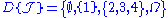is a π-system and 
is a Dynkin system with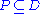 
, then 
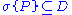. In other words, the σ-algebra generated by 
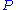is contained in 
.
One application of Dynkin's π-λ theorem is the uniqueness of the Lebesgue measure
:
Let (Ω, B, λ) be the unit interval
[0,1] with the Lebesgue measure on Borel sets. Let μ be another measure
on Ω satisfying μ[(a,b)] = b - a, and let D be the family of sets S such that μ[S] = λ[S]. Let I = { (a,b),[a,b),(a,b],[a,b] : 0 < a ≤ b < 1 }, and observe that I is closed under finite intersections, that I ⊂ D, and that B is the σ-algebra generated by I. One easily shows D satisfies the above conditions for a Dynkin-system. From Dynkin's lemma
it follows that D is in fact all of B, which is equivalent to showing that the Lebesgue measure is unique.
Eugene Dynkin
Eugene Borisovich Dynkin is a Soviet and American mathematician. He has made contributions to the fields of probability and algebra, especially semisimple Lie groups, Lie algebras, and Markov processes...
, is a collection
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
of subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of another universal set
satisfying a set of axiomAxiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s weaker than those of σ-algebra. Dynkin systems are sometimes referred to as λ-systems (Dynkin himself used this term) or d-system. These set families have applications in measure theory.
Definitions
Let Ω be a nonempty set, and let be a collection of subsets of Ω (i.e., is a subset of the power set of Ω). Then is a Dynkin system if
- Ω ∈
, - A, B ∈
and A ⊆ B implies B \ A ∈ 
, - A1, A2, A3, ... is a sequence of subsets in
and An ⊆ An+1 for all n ≥ 1, then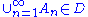 
.
Equivalently,
is a Dynkin system if
- Ω ∈
, - A ∈ D implies Ac ∈
, - A1, A2, A3, ... is a sequence of subsets in
such that Ai ∩ Aj = Ø for all i ≠ j implies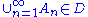 
.
An important fact is that a Dynkin system which is also a π-system
Pi system
In mathematics, a π-system on a set Ω is a set P, consisting of certain subsets of Ω, such that* P is non-empty.* A ∩ B ∈ P whenever A and B are in P....
(i.e., closed under finite intersection) is a σ-algebra.
Given any collection
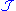of subsets of , there exists a unique Dynkin system denoted which is minimal with respect to containing 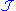. That is, if 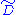is any Dynkin system containing 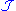, then 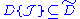. is called the Dynkin system generated by 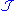. Note 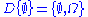. For another example, let 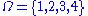and 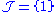; then 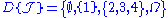.Dynkin's π-λ Theorem
If is a π-system and is a Dynkin system with 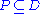, then 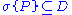. In other words, the σ-algebra generated by 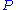is contained in .One application of Dynkin's π-λ theorem is the uniqueness of the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
:
Let (Ω, B, λ) be the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0,1] with the Lebesgue measure on Borel sets. Let μ be another measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on Ω satisfying μ[(a,b)] = b - a, and let D be the family of sets S such that μ[S] = λ[S]. Let I = { (a,b),[a,b),(a,b],[a,b] : 0 < a ≤ b < 1 }, and observe that I is closed under finite intersections, that I ⊂ D, and that B is the σ-algebra generated by I. One easily shows D satisfies the above conditions for a Dynkin-system. From Dynkin's lemma
Doob–Dynkin lemma
In mathematics, the Doob–Dynkin lemma, named after Joseph Doob and Eugene Dynkin, is a statement in probability theory that characterizes the situation when one random variable is a function of another, in terms of measurability and \sigma algebras....
it follows that D is in fact all of B, which is equivalent to showing that the Lebesgue measure is unique.