In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a polytope

Polytope

In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...

 (a polygon

Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

, polyhedron

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

 or tiling, for example) is isotoxal or edge-transitive if its symmetries

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

 act transitively on its edges. Informally, this means that there is only one type of edge to the object: given two edges, there is a translation, rotation and/or reflection that will move one edge to the other, while leaving the region occupied by the object unchanged.

The term isotoxal is derived from the Greek τοξον meaning arc.

Isotoxal polygons

An isotoxal polygon is an equilateral polygon, but not all equilateral polygons are isotoxal.

In general, an isotoxal 2n-gon will have D_n (*n) dihedral symmetry. A rhombus

Rhombus

In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...

 is a isotoxal polygon with D₂ (*2) symmetry.

All regular polygon

Regular polygon

A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...

s (equilateral triangle, square

Square (geometry)

In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...

, etc.) are isotoxal, having double the minimum symmetry order: a regular n-gon has D_n (*n) dihedral symmetry. A square is a isotoxal polygon with D₄ (*4) symmetry.

Example isotoxal polygons

Dihedral symmetry	D2 (*2)	D3 (*3)			D4 (*4)		D5 (*5)
Name	Rhombus Rhombus In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...	Equilateral triangle	Concave hexagon	Self-intersecting hexagon	Square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...	Convex octagon	Regular pentagon Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...	Self-intersecting (regular) pentagram Pentagram A pentagram is the shape of a five-pointed star drawn with five straight strokes...	Self-intersecting decagram
Picture

Isotoxal polyhedra and tilings

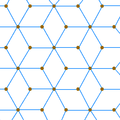The rhombille tiling is an isotoxal tiling with p6m (*632) symmetry.

An isotoxal polyhedron or tiling must be either isogonal (vertex-transitive) or isohedral (face-transitive) or both.

Regular polyhedra are isohedral (face-transitive), isogonal (vertex-transitive) and isotoxal. Quasiregular

Quasiregular polyhedron

In geometry, a quasiregular polyhedron is a semiregular polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are edge-transitive and hence step closer to regularity than the semiregular which are merely vertex-transitive.There are only two convex...

 polyhedra are isogonal and isotoxal, but not isohedral; their duals are isohedral and isotoxal, but not isogonal.

Not every polyhedron

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

 or 2-dimensional tessellation

Tessellation

A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...

 constructed from regular polygons is isotoxal. For instance, the truncated icosahedron

Truncated icosahedron

In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges....

 (the familiar soccerball) has two types of edges: hexagon-hexagon and hexagon-pentagon, and it is not possible for a symmetry of the solid to move a hexagon-hexagon edge onto a hexagon-pentagon edge.

An isotoxal polyhedron has the same dihedral angle

Dihedral angle

In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...

 for all edges.

There are nine convex isotoxal polyhedra formed from the Platonic solid

Platonic solid

In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...

s, 8 formed by the Kepler–Poinsot polyhedra, and six more as quasiregular (3 | p q) star polyhedra and their duals.

There are 5 polygonal tilings of the Euclidean plane that are isotoxal, and infinitely many isotoxal polygonal tilings of the hyperbolic plane, including the Wythoff constructions from the regular hyperbolic tilings {p,q}, and non-right (p q r) groups.

See also

• Table of polyhedron dihedral angles
  Table of polyhedron dihedral angles
  The dihedral angles for the edge-transitive polyhedra are:- References :* Coxeter, Regular Polytopes , Macmillian Company** Regular Polytopes, , Dover edition, ISBN 0-486-61480-8...
  
  
• Vertex-transitive
  Vertex-transitive
  In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
  
  
• Face-transitive
• Cell-transitive