
Ehrling's lemma
Encyclopedia
In mathematics
, Ehrling's lemma is a result concerning Banach space
s. It is often used in functional analysis
to demonstrate the equivalence of certain norms
on Sobolev space
s.
Then, for every ε > 0, there exists a constant C(ε) such that, for all x ∈ X,
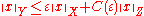
and bounded
, and let k ∈ N. Suppose that the Sobolev space Hk(Ω) is compactly embedded in Hk−1(Ω). Then the following two norms on Hk(Ω) are equivalent:
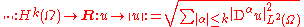
and
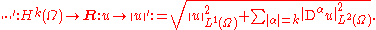
For the subspace of Hk(Ω) consisting of those Sobolev functions with zero trace
(those that are "zero on the boundary" of Ω), the L1 norm of u can be left out to yield another equivalent norm.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Ehrling's lemma is a result concerning Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s. It is often used in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
to demonstrate the equivalence of certain norms
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
on Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s.
Statement of the lemma
Let (X, ||·||X), (Y, ||·||Y) and (Z, ||·||Z) be three Banach spaces. Assume that:- X is compactly embeddedCompactly embeddedIn mathematics, the notion of being compactly embedded expresses the idea that one set or space is "well contained" inside another. There are versions of this concept appropriate to general topology and functional analysis.-Definition :...
in Y: i.e. X ⊆ Y and every ||·||X-boundedBounded functionIn mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
in X has a subsequenceSubsequenceIn mathematics, a subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements...
that is ||·||Y-convergentLimit (mathematics)In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
; and - Y is continuously embeddedContinuously embeddedIn mathematics, one normed vector space is said to be continuously embedded in another normed vector space if the inclusion function between them is continuous. In some sense, the two norms are "almost equivalent", even though they are not both defined on the same space...
in Z: i.e. Y ⊆ Z and there is a constant k so that ||y||Z ≤ k||y||Y for every y ∈ Y.
Then, for every ε > 0, there exists a constant C(ε) such that, for all x ∈ X,
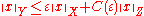
Corollary (equivalent norms for Sobolev spaces)
Let Ω ⊂ Rn be openOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
and bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
, and let k ∈ N. Suppose that the Sobolev space Hk(Ω) is compactly embedded in Hk−1(Ω). Then the following two norms on Hk(Ω) are equivalent:
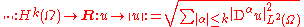
and
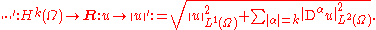
For the subspace of Hk(Ω) consisting of those Sobolev functions with zero trace
Trace operator
In mathematics, the concept of trace operator plays an important role in studying the existence and uniqueness of solutions to boundary value problems, that is, to partial differential equations with prescribed boundary conditions...
(those that are "zero on the boundary" of Ω), the L1 norm of u can be left out to yield another equivalent norm.

