Elasticity of cell membranes
Encyclopedia
A cell membrane
defines a boundary between the living cell and its environment. It consists of lipid
s, protein
s, carbohydrate
s etc. Lipids and proteins are dominant components of membranes. One of the principal types of lipids in membranes is phospholipid
. A phospholipid molecule has a polar hydrophilic head group and two hydrophobic hydrocarbon tails. When a quantity of lipid molecules disperse in water, they will assemble themselves into a bilayer in which the hydrophilic heads shield the hydrophobic tails from the water surroundings because of the hydrophobic forces
.
The widely accepted model for cell membranes is the fluid mosaic model proposed by Singer and Nicolson in 1972 [Science 175 (1972) 720]. In this model, the cell membrane
is considered as a lipid bilayer
where the lipid molecules can move freely in the membrane surface like fluid
, while the proteins are embedded in the lipid bilayer. Some proteins are called integral membrane protein
s because they traverse entirely in the lipid bilayer and play the role of information and matter communications between the interior of the cell and its outer environment. The others are called peripheral membrane protein
s because they are partially embedded in the bilayer and accomplish the other biological functions. Beneath the lipid membrane, the membrane skeleton, a network of proteins, links with the proteins in the lipid membrane.
at room temperature, and then proposed the curvature energy per unit area of the bilayer
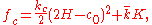(1)
where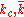
are bending rigidities. 
is called the spontaneous curvature of the membrane. 
and 
are the mean and Gaussian curvature
of the membrane surface, respectively.
The free energy
of a closed bilayer under the osmotic pressure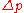
(the outer pressure minus the inner one) as:
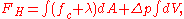(2)
where
and 
are the area element of the membrane and the volume element enclosed by the closed bilayer, respectively.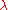 
is the surface tension of the bilayer. By taking the first order variation of above free energy, Ou-Yang and Helfrich [Phys. Rev. Lett. 59 (1987) 2486] derived an equation to describe the equilibrium shape of the bilayer as:
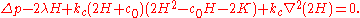(3)
They also obtained that the threshold pressure for the instability of a spherical bilayer was
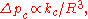(4)
where
being the radius of the spherical bilayer.
Using the shape equation (3) of closed vesilces, Ou-Yang predicted that there was a lipid torus with the ratio of two generated radii being exactly
[Phys. Rev. A 41 (1990) 4517]. His prediction was soon confirmed by the experiment [Phys. Rev. A 43 (1991) 4525]. Additionally, researchers obtained an analytical solution [Phys. Rev. E 48 (1993) 2304] to (3) which explained the classical problem---the biconcave discoidal shape of normal red cells.
is written as
(5)
where
and 
represent the arclength element and the line tension of the edge, respectively. The first order variation gives the shape equation and boundary conditions of the lipid membrane:
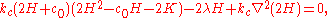(6)
(7)
(8)
(9)
where
, 
, and 
are normal curvature, geodesic curvature, and geodesic torsion of the boundary curve, respectively. 
is the unit vector perpendicular to the tangent vector of the curve and the normal vector of the membrane.
, 
, 
and 
:
(10)
where
is the in-plane strain of the membrane skeleton. Under the assumption of small deformations, and invariant between 
and 
, (10) can be expanded up to second order terms as:
(11)
where
and 
are two elastic constants. In fact, the first two terms in (11) are the bending energy of the cell membrane which contributes mainly from the lipid bilayer. The last two terms come from the entropic elasticity of the membrane skeleton.
[2] U. Seifert, Configurations of Fluid Membranes and Vesicles, Adv. Phys. 46 (1997) 13-137.
[3] Z. C. Ou-Yang, J. X. Liu and Y. Z. Xie, Geometric Methods in the Elastic Theory of Membranes in Liquid Crystal Phases (World Scientific, Singapore, 1999).
[2] O.-Y. Zhong-Can and W. Helfrich, Instability and Deformation of a Spherical Vesicle by Pressure, Phys. Rev. Lett. 59 (1987) 2486-2488.
[3] O.-Y. Zhong-Can, Anchor Ring-Vesicle Membranes, Phys. Rev. A 41 (1990) 4517-4520.
[4] H. Naito, M. Okuda, and O.-Y. Zhong-Can, Counterexample to Some Shape Equations for Axisymmetric Vesicles, Phys. Rev. E 48 (1993) 2304-2307.
[5] U. Seifert, Vesicles of toroidal topology, Phys. Rev. Lett. 66 (1991) 2404-2407.
[6] U. Seifert, K. Berndl, and R. Lipowsky, Shape transformations of vesicles: Phase diagram for spontaneous- curvature and bilayer-coupling models, Phys. Rev. A 44 (1991) 1182-1202.
[7] L. Miao etal., Budding transitions of fluid-bilayer vesicles: The effect of area-difference elasticity, Phys. Rev. E 49 (1994) 5389-5407.
[2] R. Capovilla, J. Guven, and J.A. Santiago, Lipid membranes with an edge, Phys. Rev. E 66 (2002) 021607.
[3] R. Capovilla and J. Guven, Stresses in lipid membranes, J. Phys. A 35 (2002) 6233-6247.
[4] Z. C. Tu and Z. C. Ou-Yang, Lipid membranes with free edges, Phys. Rev. E 68, (2003) 061915.
[5] T. Umeda, Y. Suezaki, K. Takiguchi, and H. Hotani, Theoretical analysis of opening-up vesicles with single and two holes, Phys. Rev. E 71 (2005) 011913.
[2] J. J. Zhou, Y. Zhang, X. Zhou, Z. C. Ou-Yang, Large Deformation of Spherical Vesicle Studied by Perturbation Theory and Surface Evolver, Int J Mod Phys B 15 (2001) 2977-2991.
[3] Y. Zhang, X. Zhou, J. J. Zhou and Z. C. Ou-Yang, Triconcave Solution to the Helfrich Variation Problem for the Shape of Lipid Bilayer Vesicles is Found by Surface Evolver, In. J. Mod. Phys. B 16 (2002) 511-517.
[4] Q. Du, C. Liu and X. Wang, Simulating the deformation of vesicle membranes under elastic bending energy in three dimensions, J. Comput. Phys. 212 (2006) 757.
[5] X. Wang and Q. Du, physics/0605095.
[2] S. K. Boey, D. H. Boal, and D. E. Discher, Simulations of the Erythrocyte Cytoskeleton at Large Deformation. I. Microscopic Models, Biophys. J. 75 (1998) 1573-1583.
[3] D. E. Discher, D. H. Boal, and S. K. Boey, Simulations of the Erythrocyte Cytoskeleton at Large Deformation. II. Micropipette Aspiration, Biophys. J. 75 (1998) 1584-1597.
[4] E. Sackmann, A.R. Bausch and L. Vonna, Physics of Composite Cell Membrane and Actin Based Cytoskeleton, in Physics of bio-molecules and cells, Edited by H. Flyvbjerg, F. Julicher, P. Ormos And F. David (Springer, Berlin, 2002).
[5] G. Lim, M. Wortis, and R. Mukhopadhyay, Stomatocyte–discocyte–echinocyte sequence of the human red blood cell: Evidence for the bilayer–couple hypothesis from membrane mechanics, Proc. Natl. Acad. Sci. 99 (2002) 16766-16769.
[6] Z. C. Tu and Z. C. Ou-Yang, A Geometric Theory on the Elasticity of Bio-membranes, J. Phys. A: Math. Gen. 37 (2004) 11407-11429.
[7] Z. C. Tu and Z. C. Ou-Yang, Elastic theory of low-dimensional continua and its applications in bio- and nano-structures,arxiv:0706.0001.
Cell membrane
The cell membrane or plasma membrane is a biological membrane that separates the interior of all cells from the outside environment. The cell membrane is selectively permeable to ions and organic molecules and controls the movement of substances in and out of cells. It basically protects the cell...
defines a boundary between the living cell and its environment. It consists of lipid
Lipid
Lipids constitute a broad group of naturally occurring molecules that include fats, waxes, sterols, fat-soluble vitamins , monoglycerides, diglycerides, triglycerides, phospholipids, and others...
s, protein
Protein
Proteins are biochemical compounds consisting of one or more polypeptides typically folded into a globular or fibrous form, facilitating a biological function. A polypeptide is a single linear polymer chain of amino acids bonded together by peptide bonds between the carboxyl and amino groups of...
s, carbohydrate
Carbohydrate
A carbohydrate is an organic compound with the empirical formula ; that is, consists only of carbon, hydrogen, and oxygen, with a hydrogen:oxygen atom ratio of 2:1 . However, there are exceptions to this. One common example would be deoxyribose, a component of DNA, which has the empirical...
s etc. Lipids and proteins are dominant components of membranes. One of the principal types of lipids in membranes is phospholipid
Phospholipid
Phospholipids are a class of lipids that are a major component of all cell membranes as they can form lipid bilayers. Most phospholipids contain a diglyceride, a phosphate group, and a simple organic molecule such as choline; one exception to this rule is sphingomyelin, which is derived from...
. A phospholipid molecule has a polar hydrophilic head group and two hydrophobic hydrocarbon tails. When a quantity of lipid molecules disperse in water, they will assemble themselves into a bilayer in which the hydrophilic heads shield the hydrophobic tails from the water surroundings because of the hydrophobic forces
Hydrophobe
In chemistry, hydrophobicity is the physical property of a molecule that is repelled from a mass of water....
.
The widely accepted model for cell membranes is the fluid mosaic model proposed by Singer and Nicolson in 1972 [Science 175 (1972) 720]. In this model, the cell membrane
Cell membrane
The cell membrane or plasma membrane is a biological membrane that separates the interior of all cells from the outside environment. The cell membrane is selectively permeable to ions and organic molecules and controls the movement of substances in and out of cells. It basically protects the cell...
is considered as a lipid bilayer
Lipid bilayer
The lipid bilayer is a thin membrane made of two layers of lipid molecules. These membranes are flat sheets that form a continuous barrier around cells. The cell membrane of almost all living organisms and many viruses are made of a lipid bilayer, as are the membranes surrounding the cell nucleus...
where the lipid molecules can move freely in the membrane surface like fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
, while the proteins are embedded in the lipid bilayer. Some proteins are called integral membrane protein
Integral membrane protein
An integral membrane protein is a protein molecule that is permanently attached to the biological membrane. Proteins that cross the membrane are surrounded by "annular" lipids, which are defined as lipids that are in direct contact with a membrane protein...
s because they traverse entirely in the lipid bilayer and play the role of information and matter communications between the interior of the cell and its outer environment. The others are called peripheral membrane protein
Peripheral membrane protein
Peripheral membrane proteins are proteins that adhere only temporarily to the biological membrane with which they are associated. These molecules attach to integral membrane proteins, or penetrate the peripheral regions of the lipid bilayer. The regulatory protein subunits of many ion channels and...
s because they are partially embedded in the bilayer and accomplish the other biological functions. Beneath the lipid membrane, the membrane skeleton, a network of proteins, links with the proteins in the lipid membrane.
Elasticity of lipid vesicles
The first step to study the elasticity of cell membranes is to study lipid bilayers. Usually, the thickness of the lipid bilayer is much smaller than the scale of the whole lipid bilayer. It is reasonable to describe the lipid bilayer by a mathematical surface. In 1973, Helfrich [Z. Naturforsch. C 28 (1973) 693] recognized that the lipid bilayer was just like a nematic liquid crystalLiquid crystal
Liquid crystals are a state of matter that have properties between those of a conventional liquid and those of a solid crystal. For instance, an LC may flow like a liquid, but its molecules may be oriented in a crystal-like way. There are many different types of LC phases, which can be...
at room temperature, and then proposed the curvature energy per unit area of the bilayer
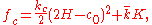(1)where
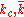are bending rigidities. is called the spontaneous curvature of the membrane. and are the mean and Gaussian curvatureGaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
of the membrane surface, respectively.
The free energy
Thermodynamic free energy
The thermodynamic free energy is the amount of work that a thermodynamic system can perform. The concept is useful in the thermodynamics of chemical or thermal processes in engineering and science. The free energy is the internal energy of a system less the amount of energy that cannot be used to...
of a closed bilayer under the osmotic pressure
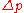(the outer pressure minus the inner one) as: 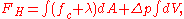(2)where
and are the area element of the membrane and the volume element enclosed by the closed bilayer, respectively. 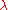is the surface tension of the bilayer. By taking the first order variation of above free energy, Ou-Yang and Helfrich [Phys. Rev. Lett. 59 (1987) 2486] derived an equation to describe the equilibrium shape of the bilayer as: 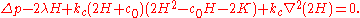(3)They also obtained that the threshold pressure for the instability of a spherical bilayer was
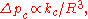(4)where
being the radius of the spherical bilayer.Using the shape equation (3) of closed vesilces, Ou-Yang predicted that there was a lipid torus with the ratio of two generated radii being exactly
[Phys. Rev. A 41 (1990) 4517]. His prediction was soon confirmed by the experiment [Phys. Rev. A 43 (1991) 4525]. Additionally, researchers obtained an analytical solution [Phys. Rev. E 48 (1993) 2304] to (3) which explained the classical problem---the biconcave discoidal shape of normal red cells.Elasticity of open lipid membranes
The opening-up process of lipid bilayers by talin was observed by Saitoh et al. [Proc. Natl. Acad. Sci. 95 (1998) 1026] arose the interest of studying the equilibrium shape equation and boundary conditions of lipid bilayers with free exposed edges. Capovilla et al. [Phys. Rev. E 66 (2002) 021607], Tu and Ou-Yang [Phys. Rev. E 68 (2003) 061915] carefully studied this problem. The free energy of a lipid membrane with an edge is written as (5)where
and represent the arclength element and the line tension of the edge, respectively. The first order variation gives the shape equation and boundary conditions of the lipid membrane: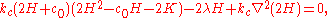 (6) (7) (8) (9)where
, , and are normal curvature, geodesic curvature, and geodesic torsion of the boundary curve, respectively. is the unit vector perpendicular to the tangent vector of the curve and the normal vector of the membrane.Elasticity of cell membranes
A cell membrane is simplified as lipid bilayer plus membrane skeleton. The skeleton is a cross-linking protein network and joints to the bilayer at some points. Assume that each proteins in the membrane skeleton have similar length which is much smaller than the whole size of the cell membrane, and that the membrane is locally 2-dimensional uniform and homogenous. Thus the free energy density can be expressed as the invariant form of, , and : (10)where
is the in-plane strain of the membrane skeleton. Under the assumption of small deformations, and invariant between and , (10) can be expanded up to second order terms as: (11)where
and are two elastic constants. In fact, the first two terms in (11) are the bending energy of the cell membrane which contributes mainly from the lipid bilayer. The last two terms come from the entropic elasticity of the membrane skeleton.Reviews on configurations of lipid vesicles
[1] R. Lipowsky, The Conformation of Membranes, Nature 349 (1991) 475-481.[2] U. Seifert, Configurations of Fluid Membranes and Vesicles, Adv. Phys. 46 (1997) 13-137.
[3] Z. C. Ou-Yang, J. X. Liu and Y. Z. Xie, Geometric Methods in the Elastic Theory of Membranes in Liquid Crystal Phases (World Scientific, Singapore, 1999).
Research papers on closed vesicles
[1] W. Helfrich, Elastic Properties of Lipid Bilayers—Theory and Possible Experiments, Z. Naturforsch. C 28 (1973) 693-703.[2] O.-Y. Zhong-Can and W. Helfrich, Instability and Deformation of a Spherical Vesicle by Pressure, Phys. Rev. Lett. 59 (1987) 2486-2488.
[3] O.-Y. Zhong-Can, Anchor Ring-Vesicle Membranes, Phys. Rev. A 41 (1990) 4517-4520.
[4] H. Naito, M. Okuda, and O.-Y. Zhong-Can, Counterexample to Some Shape Equations for Axisymmetric Vesicles, Phys. Rev. E 48 (1993) 2304-2307.
[5] U. Seifert, Vesicles of toroidal topology, Phys. Rev. Lett. 66 (1991) 2404-2407.
[6] U. Seifert, K. Berndl, and R. Lipowsky, Shape transformations of vesicles: Phase diagram for spontaneous- curvature and bilayer-coupling models, Phys. Rev. A 44 (1991) 1182-1202.
[7] L. Miao etal., Budding transitions of fluid-bilayer vesicles: The effect of area-difference elasticity, Phys. Rev. E 49 (1994) 5389-5407.
Research papers on open membranes
[1] A. Saitoh, K. Takiguchi, Y. Tanaka, and H. Hotani, Opening-up of liposomal membranes by talin, Proc. Natl. Acad. Sci. 95 (1998) 1026-1031.[2] R. Capovilla, J. Guven, and J.A. Santiago, Lipid membranes with an edge, Phys. Rev. E 66 (2002) 021607.
[3] R. Capovilla and J. Guven, Stresses in lipid membranes, J. Phys. A 35 (2002) 6233-6247.
[4] Z. C. Tu and Z. C. Ou-Yang, Lipid membranes with free edges, Phys. Rev. E 68, (2003) 061915.
[5] T. Umeda, Y. Suezaki, K. Takiguchi, and H. Hotani, Theoretical analysis of opening-up vesicles with single and two holes, Phys. Rev. E 71 (2005) 011913.
Numerical solutions on lipid membranes
[1] J. Yan, Q. H. Liu, J. X. Liu and Z. C. Ou-Yang, Numerical observation of nonaxisymmetric vesicles in fluid membranes, Phys. Rev. E 58 (1998) 4730-4736.[2] J. J. Zhou, Y. Zhang, X. Zhou, Z. C. Ou-Yang, Large Deformation of Spherical Vesicle Studied by Perturbation Theory and Surface Evolver, Int J Mod Phys B 15 (2001) 2977-2991.
[3] Y. Zhang, X. Zhou, J. J. Zhou and Z. C. Ou-Yang, Triconcave Solution to the Helfrich Variation Problem for the Shape of Lipid Bilayer Vesicles is Found by Surface Evolver, In. J. Mod. Phys. B 16 (2002) 511-517.
[4] Q. Du, C. Liu and X. Wang, Simulating the deformation of vesicle membranes under elastic bending energy in three dimensions, J. Comput. Phys. 212 (2006) 757.
[5] X. Wang and Q. Du, physics/0605095.
Selected papers on cell membranes
[1] Y. C. Fung and P. Tong, Theory of the Sphering of Red Blood Cells, Biophys. J. 8 (1968) 175-198.[2] S. K. Boey, D. H. Boal, and D. E. Discher, Simulations of the Erythrocyte Cytoskeleton at Large Deformation. I. Microscopic Models, Biophys. J. 75 (1998) 1573-1583.
[3] D. E. Discher, D. H. Boal, and S. K. Boey, Simulations of the Erythrocyte Cytoskeleton at Large Deformation. II. Micropipette Aspiration, Biophys. J. 75 (1998) 1584-1597.
[4] E. Sackmann, A.R. Bausch and L. Vonna, Physics of Composite Cell Membrane and Actin Based Cytoskeleton, in Physics of bio-molecules and cells, Edited by H. Flyvbjerg, F. Julicher, P. Ormos And F. David (Springer, Berlin, 2002).
[5] G. Lim, M. Wortis, and R. Mukhopadhyay, Stomatocyte–discocyte–echinocyte sequence of the human red blood cell: Evidence for the bilayer–couple hypothesis from membrane mechanics, Proc. Natl. Acad. Sci. 99 (2002) 16766-16769.
[6] Z. C. Tu and Z. C. Ou-Yang, A Geometric Theory on the Elasticity of Bio-membranes, J. Phys. A: Math. Gen. 37 (2004) 11407-11429.
[7] Z. C. Tu and Z. C. Ou-Yang, Elastic theory of low-dimensional continua and its applications in bio- and nano-structures,arxiv:0706.0001.