
Elkies trinomial curves
Encyclopedia
In number theory
, the Elkies trinomial curves are certain hyperelliptic curves constructed by Noam Elkies
which have the property that rational points on them correspond to trinomial polynomials giving an extension of Q with particular Galois group
s.
One curve, C168, gives Galois group PSL(2,7)
from a polynomial of degree seven, and the other, C1344, gives Galois group AL(8), the semidirect product
of a 2-elementary group of order eight acted on by PSL(2, 7), giving a transitive permutation subgroup of the symmetric group on eight roots of order 1344.
The equation of the curve C168 is
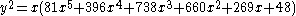
The curve is a plane algebraic curve
model for a Galois resolvent for the trinomial polynomial equation x7 + bx + c = 0. If there exists a point (x, y) on the (projectivized) curve, there is a corresponding pair (b, c) of rational numbers, such that the trinomial polynomial either factors or has Galois group PSL(2,7), the finite simple group of order 168. The curve has genus
two, and so by Faltings theorem there are only a finite number of rational points on it. These rational points were proven by Nils Bruin using the computer program Kash
to be the only ones on C168, and they give only four distinct trinomial polynomials with Galois group PSL(2,7): x7-7x+3 (the Trinks polynomial), (1/11)x7-14x+32 (the Erbach-Fisher-McKay polynomial) and two new polynomials with Galois group PSL(2,7),
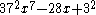
and
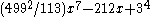 .
.
On the other hand, the equation of curve C1344 is
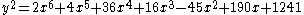
Once again the genus is two, and by Faltings theorem the list of rational points is finite. It is thought the only rational points on it correspond to polynomials x8+16x+28, x8+576x+1008, 19453x8+19x+2 which have Galois group AL(8), and x8+324x+567, which comes from two different rational points and has Galois group PSL(2, 7) again, this time as the Galois group of a polynomial of degree eight.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the Elkies trinomial curves are certain hyperelliptic curves constructed by Noam Elkies
Noam Elkies
Noam David Elkies is an American mathematician and chess master.At age 14, Elkies received a gold medal with a perfect score at the International Mathematical Olympiad, the youngest ever to do so...
which have the property that rational points on them correspond to trinomial polynomials giving an extension of Q with particular Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
s.
One curve, C168, gives Galois group PSL(2,7)
PSL(2,7)
In mathematics, the projective special linear group PSL is a finite simple group that has important applications in algebra, geometry, and number theory. It is the automorphism group of the Klein quartic as well as the symmetry group of the Fano plane...
from a polynomial of degree seven, and the other, C1344, gives Galois group AL(8), the semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of a 2-elementary group of order eight acted on by PSL(2, 7), giving a transitive permutation subgroup of the symmetric group on eight roots of order 1344.
The equation of the curve C168 is
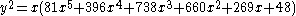
The curve is a plane algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
model for a Galois resolvent for the trinomial polynomial equation x7 + bx + c = 0. If there exists a point (x, y) on the (projectivized) curve, there is a corresponding pair (b, c) of rational numbers, such that the trinomial polynomial either factors or has Galois group PSL(2,7), the finite simple group of order 168. The curve has genus
Geometric genus
In algebraic geometry, the geometric genus is a basic birational invariant pg of algebraic varieties and complex manifolds.-Definition:...
two, and so by Faltings theorem there are only a finite number of rational points on it. These rational points were proven by Nils Bruin using the computer program Kash
KASH
Kash, Kaš or KASH may refer to:*the Egyptian name of Lower Nubia*the Nubian kingdom of Kush* KASH, the command line interface of the KANT computer algebra system* Slang term among cannabis users for hashish covered with kief...
to be the only ones on C168, and they give only four distinct trinomial polynomials with Galois group PSL(2,7): x7-7x+3 (the Trinks polynomial), (1/11)x7-14x+32 (the Erbach-Fisher-McKay polynomial) and two new polynomials with Galois group PSL(2,7),
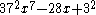
and
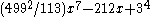 .
.On the other hand, the equation of curve C1344 is
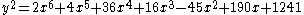
Once again the genus is two, and by Faltings theorem the list of rational points is finite. It is thought the only rational points on it correspond to polynomials x8+16x+28, x8+576x+1008, 19453x8+19x+2 which have Galois group AL(8), and x8+324x+567, which comes from two different rational points and has Galois group PSL(2, 7) again, this time as the Galois group of a polynomial of degree eight.

