Engel expansion
Encyclopedia
The Engel expansion of a positive real number
x is the unique non-decreasing sequence of positive integer
s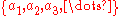
such that
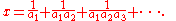
Rational number
s have a finite Engel expansion, while irrational number
s have an infinite Engel expansion. If x is rational, its Engel expansion provides a representation of x as an Egyptian fraction. Engel expansions are named after Friedrich Engel
, who studied them in 1913.
An expansion analogous to an Engel expansion, in which alternating terms are negative, is called a Pierce expansion.
:
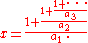
They claim that ascending continued fractions such as this have been studied as early as Fibonacci
's Liber Abaci
(1202). This claim appears to refer to Fibonacci's compound fraction notation in which a sequence of numerators and denominators sharing the same fraction bar represents an ascending continued fraction:
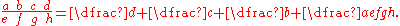
If such a notation has all numerators 0 or 1, as occurs in several instances in Liber Abaci
, the result is an Engel expansion. However, Engel expansion as a general technique does not seem to be described by Fibonacci.
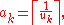
and
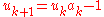
where
is the ceiling function (the smallest integer not less than r).
If
for any i, halt the algorithm.
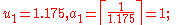
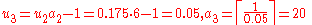
The series ends here. Thus,
and the Engel expansion of 1.175 is {1, 6, 20}.
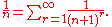
the final digit n in a finite Engel expansion can be replaced by an infinite sequence of (n + 1)s without changing its value. For example
This is analogous to the fact that any rational number with a finite decimal representation also has an infinite decimal representation (see 0.999...
).
Erdős
, Rényi
, and Szüsz asked for nontrivial bounds on the length of the finite Engel expansion of a rational number x/y; this question was answered by Erdős and Shallit
, who proved that the number of terms in the expansion is O(y1/3 + ε) for any ε > 0.
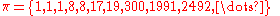
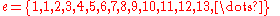
And in general,
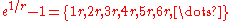
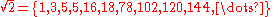
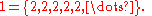
In general, an Engel expansion with constant terms is a geometric series.
More Engel expansions for constants can be found here.
; more precisely, for almost all
numbers in the interval (0,1], the limit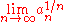
exists and is equal to e
. However, the subset of the interval for which this is not the case is still large enough that its Hausdorff dimension
is one.
The same typical growth rate applies to the terms in expansion generated by the greedy algorithm for Egyptian fractions
. However, the set of real numbers in the interval (0,1] whose Engel expansions coincide with their greedy expansions has measure zero, and Hausdorff dimension 1/2.
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
x is the unique non-decreasing sequence of positive integer
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s
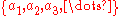such that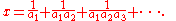Rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s have a finite Engel expansion, while irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s have an infinite Engel expansion. If x is rational, its Engel expansion provides a representation of x as an Egyptian fraction. Engel expansions are named after Friedrich Engel
Friedrich Engel (mathematician)
Friedrich Engel was a German mathematician.Engel was born in Lugau, Saxony, as the son of a Lutheran pastor. He attended the Universities of both Leipzig and Berlin, before receiving his doctorate from Leipzig in 1883.Engel studied under Felix Klein at Leipzig, and collaborated with Sophus Lie for...
, who studied them in 1913.
An expansion analogous to an Engel expansion, in which alternating terms are negative, is called a Pierce expansion.
Engel expansions, continued fractions, and Fibonacci
Kraaikamp and Wu (2004) observe that an Engel expansion can also be written as an ascending variant of a continued fractionContinued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
:
They claim that ascending continued fractions such as this have been studied as early as Fibonacci
Fibonacci
Leonardo Pisano Bigollo also known as Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, or, most commonly, simply Fibonacci, was an Italian mathematician, considered by some "the most talented western mathematician of the Middle Ages."Fibonacci is best known to the modern...
's Liber Abaci
Liber Abaci
Liber Abaci is a historic book on arithmetic by Leonardo of Pisa, known later by his nickname Fibonacci...
(1202). This claim appears to refer to Fibonacci's compound fraction notation in which a sequence of numerators and denominators sharing the same fraction bar represents an ascending continued fraction:
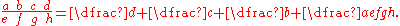
If such a notation has all numerators 0 or 1, as occurs in several instances in Liber Abaci
Liber Abaci
Liber Abaci is a historic book on arithmetic by Leonardo of Pisa, known later by his nickname Fibonacci...
, the result is an Engel expansion. However, Engel expansion as a general technique does not seem to be described by Fibonacci.
Algorithm for computing Engel expansions
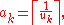
To find the Engel expansion of x, letand
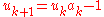
where
is the ceiling function (the smallest integer not less than r).If
for any i, halt the algorithm.Example
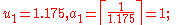
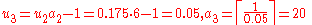
To find the Engel expansion of 1.175, we perform the following steps.The series ends here. Thus,
and the Engel expansion of 1.175 is {1, 6, 20}.
Engel expansions of rational numbers
Every positive rational number has a unique finite Engel expansion. In the algorithm for Engel expansion, if ui is a rational number x/y, then ui+1 = (−y mod x)/y. Therefore, at each step, the numerator in the remaining fraction ui decreases and the process of constructing the Engel expansion must terminate in a finite number of steps. Every rational number also has a unique infinite Engel expansion: using the identity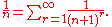the final digit n in a finite Engel expansion can be replaced by an infinite sequence of (n + 1)s without changing its value. For example
This is analogous to the fact that any rational number with a finite decimal representation also has an infinite decimal representation (see 0.999...
0.999...
In mathematics, the repeating decimal 0.999... denotes a real number that can be shown to be the number one. In other words, the symbols 0.999... and 1 represent the same number...
).
Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
, Rényi
Alfréd Rényi
Alfréd Rényi was a Hungarian mathematician who made contributions in combinatorics, graph theory, number theory but mostly in probability theory.-Life:...
, and Szüsz asked for nontrivial bounds on the length of the finite Engel expansion of a rational number x/y; this question was answered by Erdős and Shallit
Jeffrey Shallit
Jeffrey Outlaw Shallit is a computer scientist, number theorist, a noted advocate for civil liberties on the Internet, and a noted critic of intelligent design. He is married to Anna Lubiw, also a computer scientist....
, who proved that the number of terms in the expansion is O(y1/3 + ε) for any ε > 0.
Engel expansions for some well-known constants
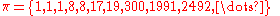
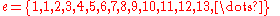
And in general,
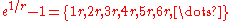
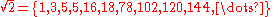
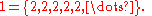
In general, an Engel expansion with constant terms is a geometric series.
More Engel expansions for constants can be found here.
Growth rate of the expansion terms
The coefficients ai of the Engel expansion typically exhibit exponential growthExponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
; more precisely, for almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
numbers in the interval (0,1], the limit
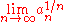exists and is equal to eE (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
. However, the subset of the interval for which this is not the case is still large enough that its Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
is one.
The same typical growth rate applies to the terms in expansion generated by the greedy algorithm for Egyptian fractions
Greedy algorithm for Egyptian fractions
In mathematics, the greedy algorithm for Egyptian fractions is a greedy algorithm, first described by Fibonacci, for transforming rational numbers into Egyptian fractions. An Egyptian fraction is a representation of an irreducible fraction as a sum of unit fractions, as e.g. 5/6 = 1/2 + 1/3...
. However, the set of real numbers in the interval (0,1] whose Engel expansions coincide with their greedy expansions has measure zero, and Hausdorff dimension 1/2.