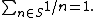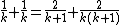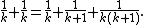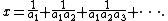Egyptian fraction
Encyclopedia
An Egyptian fraction is the sum of distinct unit fraction
s, such as
. That is, each fraction
in the expression has a numerator equal to 1 and a denominator that is a positive integer
, and all the denominators differ from each other. The sum of an expression of this type is a positive rational number
a/b; for instance the Egyptian fraction above sums to 43/48. Every positive rational number can be represented by an Egyptian fraction. Sums of this type, and similar sums also including 2/3 and 3/4 as summands, were used as a serious notation for rational numbers by the ancient Egyptians, and continued to be used by other civilizations into medieval times. In modern mathematical notation, Egyptian fractions have been superseded by vulgar fractions and decimal
notation. However, Egyptian fractions continue to be an object of study in modern number theory
and recreational mathematics
, as well as in modern historical studies of ancient mathematics.
Egyptian fraction notation was developed in the Middle Kingdom of Egypt
, altering the Old Kingdom's Eye of Horus
numeration system. Five early texts in which Egyptian fractions appear were the Egyptian Mathematical Leather Roll
, the Moscow Mathematical Papyrus
, the Reisner Papyrus
, the Kahun Papyrus
and the Akhmim Wooden Tablet
. A later text, the Rhind Mathematical Papyrus
, introduced improved ways of writing Egyptian fractions. The Rhind papyrus was written by Ahmes
and dates from the Second Intermediate Period; it includes a table of Egyptian fraction expansions for rational numbers 2/n, as well as 84 word problems
. Solutions to each problem were written out in scribal shorthand, with the final answers of all 84 problems being expressed in Egyptian fraction notation. 2/n tables similar to the one on the Rhind papyrus also appear on some of the other texts. However, as the Kahun Papyrus
shows, vulgar fractions were also used by scribes within their calculations.
D21
(er, "[one] among" or possibly re, mouth) above a number to represent the reciprocal
of that number. Similarly in hieratic script they drew a line over the letter representing the number. For example:
The Egyptians had special symbols for 1/2, 2/3, and 3/4 that were used to reduce the size of numbers greater than 1/2 when such numbers were converted to an Egyptian fraction series. The remaining number after subtracting one of these special fractions was written using as a sum of distinct unit fractions according to the usual Egyptian fraction notation.
The Egyptians also used an alternative notation modified from the Old Kingdom and based on the parts of the Eye of Horus
to denote a special set of fractions of the form 1/2k (for k = 1, 2, ..., 6) and sums of these numbers, which are necessarily dyadic rational numbers
. These "Horus-Eye fractions" were used in the Middle Kingdom in conjunction with the later notation for Egyptian fractions to subdivide a hekat, the primary ancient Egyptian volume measure for grain, bread, and other small quantities of volume, as described in the Akhmim Wooden Tablet
. If any remainder was left after expressing a quantity in Eye of Horus fractions of a hekat, the remainder was written using the usual Egyptian fraction notation as multiples of a ro, a unit equal to 1/320 of a hekat.
and for composite
denominators, and more than one method was used for numbers of each type:
Egyptian fraction notation continued to be used in Greek times and into the Middle Ages , despite complaints as early as Ptolemy
's Almagest
about the clumsiness of the notation compared to alternatives such as the Babylonian base-60 notation
. An important text of medieval mathematics, the Liber Abaci
(1202) of Leonardo of Pisa (more commonly known as Fibonacci), provides some insight into the uses of Egyptian fractions in the Middle Ages, and introduces topics that continue to be important in modern mathematical study of these series.
The primary subject of the Liber Abaci is calculations involving decimal and vulgar fraction notation, which eventually replaced Egyptian fractions. Fibonacci himself used a complex notation for fractions involving a combination of a mixed radix
notation with sums of fractions. Many of the calculations throughout Fibonacci's book involve numbers represented as Egyptian fractions, and one section of this book provides a list of method for conversion of vulgar fractions to Egyptian fractions. If the number is not already a unit fraction, the first method in this list is to attempt to split the numerator into a sum of divisors of the denominator; this is possible whenever the denominator is a practical number
, and Liber Abaci includes tables of expansions of this type for the practical numbers 6, 8, 12, 20, 24, 60, and 100.
The next several methods involve algebraic identities such as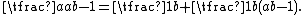
For instance, Fibonacci represents the fraction 
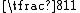by splitting the numerator into a sum of two numbers, each of which divides one plus the denominator: 
Fibonacci applies the algebraic identity above to each these two parts, producing the expansion
Fibonacci describes similar methods for denominators that are two or three less than a number with many factors.
In the rare case that these other methods all fail, Fibonacci suggests a greedy algorithm
for computing Egyptian fractions, in which one repeatedly chooses the unit fraction with the smallest denominator that is no larger than the remaining fraction to be expanded: that is, in more modern notation, we replace a fraction x/y by the expansion
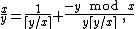
where
represents the ceiling function.
Fibonacci suggests switching to another method after the first such expansion, but he also gives examples in which this greedy expansion was iterated until a complete Egyptian fraction expansion was constructed:
and 
As later mathematicians showed, each greedy expansion reduces the numerator of the remaining fraction to be expanded, so this method always terminates with a finite expansion. However, compared to ancient Egyptian expansions or to more modern methods, this method may produce expansions that are quite long, with large denominators, and Fibonacci himself noted the awkwardness of the expansions produced by this method. For instance, the greedy method expands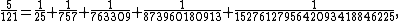
while other methods lead to the much better expansion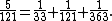
Sylvester's sequence
2, 3, 7, 43, 1807, ... can be viewed as generated by an infinite greedy expansion of this type for the number one, where at each step we choose the denominator
instead of 
, and sometimes Fibonacci's greedy algorithm is attributed to Sylvester
.
After his description of the greedy algorithm, Fibonacci suggests yet another method, expanding a fraction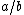
by searching for a number c having many divisors, with 
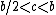, replacing 
by 
, and expanding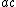 
as a sum of divisors of 
, similar to the method proposed by Hultsch and Bruins to explain the ancient RMP 2/p expansions.
Modern number theorists have studied many different problems related to Egyptian fractions, including problems of bounding the length or maximum denominator in Egyptian fraction representations, finding expansions of certain special forms or in which the denominators are all of some special type, the termination of various methods for Egyptian fraction expansion, and showing that expansions exist for any sufficiently dense set of sufficiently smooth number
s.
Unit fraction
A unit fraction is a rational number written as a fraction where the numerator is one and the denominator is a positive integer. A unit fraction is therefore the reciprocal of a positive integer, 1/n...
s, such as
. That is, each fractionFraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
in the expression has a numerator equal to 1 and a denominator that is a positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, and all the denominators differ from each other. The sum of an expression of this type is a positive rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
a/b; for instance the Egyptian fraction above sums to 43/48. Every positive rational number can be represented by an Egyptian fraction. Sums of this type, and similar sums also including 2/3 and 3/4 as summands, were used as a serious notation for rational numbers by the ancient Egyptians, and continued to be used by other civilizations into medieval times. In modern mathematical notation, Egyptian fractions have been superseded by vulgar fractions and decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
notation. However, Egyptian fractions continue to be an object of study in modern number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
and recreational mathematics
Recreational mathematics
Recreational mathematics is an umbrella term, referring to mathematical puzzles and mathematical games.Not all problems in this field require a knowledge of advanced mathematics, and thus, recreational mathematics often attracts the curiosity of non-mathematicians, and inspires their further study...
, as well as in modern historical studies of ancient mathematics.
Ancient Egypt
- For more information on this subject, see Egyptian numeralsEgyptian numeralsThe system of Ancient Egyptian numerals was used in Ancient Egypt until the early first millennium AD. It was a decimal system, often rounded off to the higher power, written in hieroglyphs. The hieratic form of numerals stressed an exact finite series notation, ciphered one to one onto the...
, Eye of HorusEye of HorusThe Eye of Horus is an ancient Egyptian symbol of protection, royal power and good health. The eye is personified in the goddess Wadjet...
, and Egyptian mathematicsEgyptian mathematicsEgyptian mathematics is the mathematics that was developed and used in Ancient Egypt from ca. 3000 BC to ca. 300 BC.-Overview:Written evidence of the use of mathematics dates back to at least 3000 BC with the ivory labels found at Tomb Uj at Abydos. These labels appear to have been used as tags for...
.
Egyptian fraction notation was developed in the Middle Kingdom of Egypt
Middle Kingdom of Egypt
The Middle Kingdom of Egypt is the period in the history of ancient Egypt stretching from the establishment of the Eleventh Dynasty to the end of the Fourteenth Dynasty, between 2055 BC and 1650 BC, although some writers include the Thirteenth and Fourteenth dynasties in the Second Intermediate...
, altering the Old Kingdom's Eye of Horus
Eye of Horus
The Eye of Horus is an ancient Egyptian symbol of protection, royal power and good health. The eye is personified in the goddess Wadjet...
numeration system. Five early texts in which Egyptian fractions appear were the Egyptian Mathematical Leather Roll
Egyptian Mathematical Leather Roll
The Egyptian Mathematical Leather Roll was a 10 × 17 in leather roll purchased by Alexander Henry Rhind in 1858...
, the Moscow Mathematical Papyrus
Moscow Mathematical Papyrus
The Moscow Mathematical Papyrus is an ancient Egyptian mathematical papyrus, also called the Golenishchev Mathematical Papyrus, after its first owner, Egyptologist Vladimir Golenishchev. Golenishchev bought the papyrus in 1892 or 1893 in Thebes...
, the Reisner Papyrus
Reisner Papyrus
The Reisner Papyri date to the reign of Senusret I, who was king of Ancient Egypt in the 19th century BCE. The documents were discovered by Dr. G.A. Reisner during excavations in 1901-04 in Naga ed-Deir in southern Egypt. A total of four papyrusrolls were found in a wooden coffin in a tomb. * The...
, the Kahun Papyrus
Kahun Papyrus
The Kahun Papyri are a collection of ancient Egyptian texts discussing administrative, mathematical and medical topics. Its many fragments were discovered by Flinders Petrie in 1889 and are kept at the University College London. This collection of papyri is one of the largest ever found. Most of...
and the Akhmim Wooden Tablet
Akhmim wooden tablet
The Akhmim wooden tablets or Cairo wooden tablets are two ancient Egyptian wooden writing tablets. They each measure about 18 by 10 inches and are covered with plaster. The tablets are inscribed on both sides. The inscriptions on the first tablet includes a list of servants, which is followed...
. A later text, the Rhind Mathematical Papyrus
Rhind Mathematical Papyrus
The Rhind Mathematical Papyrus , is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1650 BC...
, introduced improved ways of writing Egyptian fractions. The Rhind papyrus was written by Ahmes
Ahmes
Ahmes was an ancient Egyptian scribe who lived during the Second Intermediate Period and the beginning of the Eighteenth Dynasty . He wrote the Rhind Mathematical Papyrus, a work of Ancient Egyptian mathematics that dates to approximately 1650 BC; he is the earliest contributor to mathematics...
and dates from the Second Intermediate Period; it includes a table of Egyptian fraction expansions for rational numbers 2/n, as well as 84 word problems
Word problem (mathematics education)
In mathematics education, the term word problem is often used to refer to any math exercise where significant background information on the problem is presented as text rather than in mathematical notation...
. Solutions to each problem were written out in scribal shorthand, with the final answers of all 84 problems being expressed in Egyptian fraction notation. 2/n tables similar to the one on the Rhind papyrus also appear on some of the other texts. However, as the Kahun Papyrus
Kahun Papyrus
The Kahun Papyri are a collection of ancient Egyptian texts discussing administrative, mathematical and medical topics. Its many fragments were discovered by Flinders Petrie in 1889 and are kept at the University College London. This collection of papyri is one of the largest ever found. Most of...
shows, vulgar fractions were also used by scribes within their calculations.
Notation
To write the unit fractions used in their Egyptian fraction notation, in hieroglyph script, the Egyptians placed the hieroglyphEgyptian hieroglyphs
Egyptian hieroglyphs were a formal writing system used by the ancient Egyptians that combined logographic and alphabetic elements. Egyptians used cursive hieroglyphs for religious literature on papyrus and wood...
(er, "
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of that number. Similarly in hieratic script they drew a line over the letter representing the number. For example:
 |
 |
The Egyptians had special symbols for 1/2, 2/3, and 3/4 that were used to reduce the size of numbers greater than 1/2 when such numbers were converted to an Egyptian fraction series. The remaining number after subtracting one of these special fractions was written using as a sum of distinct unit fractions according to the usual Egyptian fraction notation.
 |
 |
 |
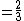The Egyptians also used an alternative notation modified from the Old Kingdom and based on the parts of the Eye of Horus
Eye of Horus
The Eye of Horus is an ancient Egyptian symbol of protection, royal power and good health. The eye is personified in the goddess Wadjet...
to denote a special set of fractions of the form 1/2k (for k = 1, 2, ..., 6) and sums of these numbers, which are necessarily dyadic rational numbers
Dyadic rational
In mathematics, a dyadic fraction or dyadic rational is a rational number whose denominator is a power of two, i.e., a number of the form a/2b where a is an integer and b is a natural number; for example, 1/2 or 3/8, but not 1/3...
. These "Horus-Eye fractions" were used in the Middle Kingdom in conjunction with the later notation for Egyptian fractions to subdivide a hekat, the primary ancient Egyptian volume measure for grain, bread, and other small quantities of volume, as described in the Akhmim Wooden Tablet
Akhmim wooden tablet
The Akhmim wooden tablets or Cairo wooden tablets are two ancient Egyptian wooden writing tablets. They each measure about 18 by 10 inches and are covered with plaster. The tablets are inscribed on both sides. The inscriptions on the first tablet includes a list of servants, which is followed...
. If any remainder was left after expressing a quantity in Eye of Horus fractions of a hekat, the remainder was written using the usual Egyptian fraction notation as multiples of a ro, a unit equal to 1/320 of a hekat.
Calculation methods
Modern historians of mathematics have studied the Rhind papyrus and other ancient sources in an attempt to discover the methods the Egyptians used in calculating with Egyptian fractions. In particular, study in this area has concentrated on understanding the tables of expansions for numbers of the form 2/n in the Rhind papyrus. Although these expansions can generally be described as algebraic identities, they do not match any single identity; rather, different methods were used for primePrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
and for composite
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
denominators, and more than one method was used for numbers of each type:
- For small odd prime denominators p, the expansion 2/p = 2/(p + 1) + 2/p(p + 1) was used.
- For larger prime denominators, an expansion of the form 2/p = 1/A + (2A-p)/Ap was used, where A is a number with many divisors (such as a practical numberPractical numberIn number theory, a practical number or panarithmic number is a positive integer n such that all smaller positive integers can be represented as sums of distinct divisors of n...
) in the range p/2 < A < p. The remaining term (2A-p)/Ap was expanded by representing the number 2A-p as a sum of divisors of A and forming a fraction d/Ap for each such divisor d in this sum . As an example, Ahmes' expansion 2/37 = 1/24 + 1/111 + 1/296 fits this pattern, with A = 24 and 2A-p = 11 = 3+8, since 3 and 8 are divisors of 24. There may be many different expansions of this type for a given p; however, as K. S. Brown observed, the expansion chosen by the Egyptians was often the one that caused the largest denominator to be as small as possible, among all expansions fitting this pattern. - For composite denominators, factored as p×q, one can expand 2/pq using the identity 2/pq = 1/aq + 1/apq, where a = (p+1)/2. For instance, applying this method for pq = 21 gives p = 3, q = 7, and a = (3+1)/2 = 2, producing the expansion 2/21 = 1/14 + 1/42 from the Rhind papyrus. Some authors have preferred to write this expansion as 2/A × A/pq, where A = p+1 ; replacing the second term of this product by p/pq + 1/pq, applying the distributive law to the product, and simplifying leads to an expression equivalent to the first expansion described here. This method appears to have been used for many of the composite numbers in the Rhind papyrus , but there are exceptions, notably 2/35, 2/91, and 2/95 .
- One can also expand 2/pq as 1/pr + 1/qr, where r = (p+q)/2. For instance, Ahmes expands 2/35 = 1/30 + 1/42, where p = 5, q = 7, and r = (5+7)/2 = 6. Later scribes used a more general form of this expansion, n/pq = 1/pr + 1/qr, where r =(p + q)/n, which works when p + q is a multiple of n .
- For some other composite denominators, the expansion for 2/pq has the form of an expansion for 2/q with each denominator multiplied by p. For instance, 95=5×19, and 2/19 = 1/12 + 1/76 + 1/114 (as can be found using the method for primes with A = 12), so 2/95 = 1/(5×12) + 1/(5×76) + 1/(5×114) = 1/60 + 1/380 + 1/570 . This expression can be simplified as 1/380 + 1/570 = 1/228 but the Rhind papyrus uses the unsimplified form.
- The final (prime) expansion in the Rhind papyrus, 2/101, does not fit any of these forms, but instead uses an expansion 2/p = 1/p + 1/2p + 1/3p + 1/6p that may be applied regardless of the value of p. That is, 2/101 = 1/101 + 1/202 + 1/303 + 1/606. A related expansion was also used in the Egyptian Mathematical Leather Roll for several cases.
Medieval mathematics
- For more information on this subject, see Liber AbaciLiber AbaciLiber Abaci is a historic book on arithmetic by Leonardo of Pisa, known later by his nickname Fibonacci...
and Greedy algorithm for Egyptian fractionsGreedy algorithm for Egyptian fractionsIn mathematics, the greedy algorithm for Egyptian fractions is a greedy algorithm, first described by Fibonacci, for transforming rational numbers into Egyptian fractions. An Egyptian fraction is a representation of an irreducible fraction as a sum of unit fractions, as e.g. 5/6 = 1/2 + 1/3...
.
Egyptian fraction notation continued to be used in Greek times and into the Middle Ages , despite complaints as early as Ptolemy
Ptolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
's Almagest
Almagest
The Almagest is a 2nd-century mathematical and astronomical treatise on the apparent motions of the stars and planetary paths. Written in Greek by Claudius Ptolemy, a Roman era scholar of Egypt,...
about the clumsiness of the notation compared to alternatives such as the Babylonian base-60 notation
Babylonian mathematics
Babylonian mathematics refers to any mathematics of the people of Mesopotamia, from the days of the early Sumerians to the fall of Babylon in 539 BC. Babylonian mathematical texts are plentiful and well edited...
. An important text of medieval mathematics, the Liber Abaci
Liber Abaci
Liber Abaci is a historic book on arithmetic by Leonardo of Pisa, known later by his nickname Fibonacci...
(1202) of Leonardo of Pisa (more commonly known as Fibonacci), provides some insight into the uses of Egyptian fractions in the Middle Ages, and introduces topics that continue to be important in modern mathematical study of these series.
The primary subject of the Liber Abaci is calculations involving decimal and vulgar fraction notation, which eventually replaced Egyptian fractions. Fibonacci himself used a complex notation for fractions involving a combination of a mixed radix
Mixed radix
Mixed radix numeral systems are non-standard positional numeral systems in which the numerical base varies from position to position. Such numerical representation applies when a quantity is expressed using a sequence of units that are each a multiple of the next smaller one, but not by the same...
notation with sums of fractions. Many of the calculations throughout Fibonacci's book involve numbers represented as Egyptian fractions, and one section of this book provides a list of method for conversion of vulgar fractions to Egyptian fractions. If the number is not already a unit fraction, the first method in this list is to attempt to split the numerator into a sum of divisors of the denominator; this is possible whenever the denominator is a practical number
Practical number
In number theory, a practical number or panarithmic number is a positive integer n such that all smaller positive integers can be represented as sums of distinct divisors of n...
, and Liber Abaci includes tables of expansions of this type for the practical numbers 6, 8, 12, 20, 24, 60, and 100.
The next several methods involve algebraic identities such as
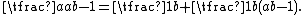For instance, Fibonacci represents the fraction 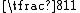by splitting the numerator into a sum of two numbers, each of which divides one plus the denominator: Fibonacci applies the algebraic identity above to each these two parts, producing the expansion Fibonacci describes similar methods for denominators that are two or three less than a number with many factors.In the rare case that these other methods all fail, Fibonacci suggests a greedy algorithm
Greedy algorithm for Egyptian fractions
In mathematics, the greedy algorithm for Egyptian fractions is a greedy algorithm, first described by Fibonacci, for transforming rational numbers into Egyptian fractions. An Egyptian fraction is a representation of an irreducible fraction as a sum of unit fractions, as e.g. 5/6 = 1/2 + 1/3...
for computing Egyptian fractions, in which one repeatedly chooses the unit fraction with the smallest denominator that is no larger than the remaining fraction to be expanded: that is, in more modern notation, we replace a fraction x/y by the expansion
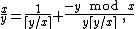
where
represents the ceiling function.Fibonacci suggests switching to another method after the first such expansion, but he also gives examples in which this greedy expansion was iterated until a complete Egyptian fraction expansion was constructed:
and As later mathematicians showed, each greedy expansion reduces the numerator of the remaining fraction to be expanded, so this method always terminates with a finite expansion. However, compared to ancient Egyptian expansions or to more modern methods, this method may produce expansions that are quite long, with large denominators, and Fibonacci himself noted the awkwardness of the expansions produced by this method. For instance, the greedy method expands
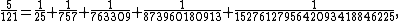
while other methods lead to the much better expansion
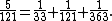
Sylvester's sequence
Sylvester's sequence
In number theory, Sylvester's sequence is an integer sequence in which each member of the sequence is the product of the previous members, plus one. The first few terms of the sequence are:...
2, 3, 7, 43, 1807, ... can be viewed as generated by an infinite greedy expansion of this type for the number one, where at each step we choose the denominator
instead of , and sometimes Fibonacci's greedy algorithm is attributed to SylvesterJames Joseph Sylvester
James Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...
.
After his description of the greedy algorithm, Fibonacci suggests yet another method, expanding a fraction
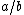by searching for a number c having many divisors, with 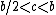, replacing by , and expanding 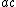as a sum of divisors of , similar to the method proposed by Hultsch and Bruins to explain the ancient RMP 2/p expansions.Modern number theory
- For more information on this subject, see Erdős–Graham conjecture, Znám's problemZnám's problemIn number theory, Znám's problem asks which sets of k integers have the property that each integer in the set is a proper divisor of the product of the other integers in the set, plus 1. Znám's problem is named after the Slovak mathematician Štefan Znám, who suggested it in 1972, although other...
, and Engel expansion.
Modern number theorists have studied many different problems related to Egyptian fractions, including problems of bounding the length or maximum denominator in Egyptian fraction representations, finding expansions of certain special forms or in which the denominators are all of some special type, the termination of various methods for Egyptian fraction expansion, and showing that expansions exist for any sufficiently dense set of sufficiently smooth number
Smooth number
In number theory, a smooth number is an integer which factors completely into small prime numbers. The term seems to have been coined by Leonard Adleman. Smooth numbers are especially important in cryptography relying on factorization.-Definition:...
s.
- The Erdős–Graham conjecture in combinatorial number theoryNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
states that, if the unit fractions are partitioned into finitely many subsets, then one of the subsets can be used to form an Egyptian fraction representation of one. That is, for every r > 0, and every r-coloring of the integers greater than one, there is a finite monochromatic subset S of these integers such that
-
- The conjecture was proven in 2003 by Ernest S. Croot, III.
- Znám's problemZnám's problemIn number theory, Znám's problem asks which sets of k integers have the property that each integer in the set is a proper divisor of the product of the other integers in the set, plus 1. Znám's problem is named after the Slovak mathematician Štefan Znám, who suggested it in 1972, although other...
and primary pseudoperfect numbers are closely related to the existence of Egyptian fractions of the form
- Znám's problem
- For instance, the primary pseudoperfect number 1806 is the product of the prime numbers 2, 3, 7, and 43, and gives rise to the Egyptian fraction 1 = 1/2 + 1/3 + 1/7 + 1/43 + 1/1806.
- Egyptian fractions are normally defined as requiring all denominators to be distinct, but this requirement can be relaxed to allow repeated denominators. However, this relaxed form of Egyptian fractions does not allow for any number to be represented using fewer fractions, as any expansion with repeated fractions can be converted to an Egyptian fraction of equal or smaller length by repeated application of the replacement
- if k is odd, or simply by replacing 1/k+1/k by 2/k if k is even. This result was first proven by .
- Graham and Jewett and proved that it is similarly possible to convert expansions with repeated denominators to (longer) Egyptian fractions, via the replacement
- This method can lead to long expansions with large denominators, such as
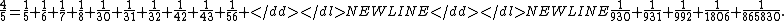
- had originally used this replacement technique to show that any rational number has Egyptian fraction representations with arbitrarily large minimum denominators.
- Any fraction x/y has an Egyptian fraction representation in which the maximum denominator is bounded by
- and a representation with at most
- terms . characterized the numbers that can be represented by Egyptian fractions in which all denominators are nth powers. In particular, a rational number q can be represented as an Egyptian fraction with square denominators if and only if q lies in one of the two half-open intervals
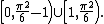showed that any rational number has very dense expansions, using a constant fraction of the denominators up to N for any sufficiently large N.
- Engel expansion, sometimes called an Egyptian product, is a form of Egyptian fraction expansion in which each denominator is a multiple of the previous one:
- In addition, the sequence of multipliers ai is required to be nondecreasing. Every rational number has a finite Engel expansion, while irrational numberIrrational numberIn mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s have an infinite Engel expansion. study numbers that have multiple distinct Egyptian fraction representations with the same number of terms and the same product of denominators; for instance, one of the examples they supply is - Unlike the ancient Egyptians, they allow denominators to be repeated in these expansions. They apply their results for this problem to the characterization of free productFree productIn mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
s of Abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s by a small number of numerical parameters: the rank of the commutator subgroupCommutator subgroupIn mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....
, the number of terms in the free product, and the product of the orders of the factors.
Open problems
- For more information on this subject, see odd greedy expansion and Erdős–Straus conjectureErdos–Straus conjectureIn number theory, the Erdős–Straus conjecture states that for all integers n ≥ 2, the rational number 4/n can be expressed as the sum of three unit fractions. Paul Erdős and Ernst G...
.
Some notable problems remain unsolved with regard to Egyptian fractions, despite considerable effort by mathematicians.
- The Erdős–Straus conjectureErdos–Straus conjectureIn number theory, the Erdős–Straus conjecture states that for all integers n ≥ 2, the rational number 4/n can be expressed as the sum of three unit fractions. Paul Erdős and Ernst G...
concerns the length of the shortest expansion for a fraction of the form 4/n. Does an expansion
-
- exist for every n? It is known to be true for all n < 1014, and for all but a vanishingly small fraction of possible values of n, but the general truth of the conjecture remains unknown.
- It is unknown whether an odd greedy expansion exists for every fraction with an odd denominator. If we modify Fibonacci's greedy method so that it always chooses the smallest possible odd denominator, under what conditions does this modified algorithm produce a finite expansion? An obvious necessary condition is that the starting fraction x/y have an odd denominator y, and it is conjectured but not known that this is also a sufficient condition. It is known that every x/y with odd y has an expansion into distinct odd unit fractions, constructed using a different method than the greedy algorithm.
- It is possible to use brute-force searchBrute-force searchIn computer science, brute-force search or exhaustive search, also known as generate and test, is a trivial but very general problem-solving technique that consists of systematically enumerating all possible candidates for the solution and checking whether each candidate satisfies the problem's...
algorithms to find the Egyptian fraction representation of a given number with the fewest possible terms or minimizing the largest denominator; however, such algorithms can be quite inefficient. The existence of polynomial time algorithms for these problems, or more generally the computational complexityComputational ComplexityComputational Complexity may refer to:*Computational complexity theory*Computational Complexity...
of such problems, remains unknown.
describes these problems in more detail and lists numerous additional open problems.
External links
... and , The Wolfram Demonstrations Project, based on programs by David EppsteinDavid EppsteinDavid Arthur Eppstein is an American computer scientist and mathematician. He is professor of computer science at University of California, Irvine. He is known for his work in computational geometry, graph algorithms, and recreational mathematics.-Biography:Born in England of New Zealander...
.- had originally used this replacement technique to show that any rational number has Egyptian fraction representations with arbitrarily large minimum denominators.
