.gif)
Entropy (arrow of time)
Encyclopedia
Entropy is the only quantity in the physical sciences (apart from certain rare interactions in particle physics; see below) that requires a particular direction for time, sometimes called an arrow of time
. As one goes "forward" in time, the second law of thermodynamics
says, the entropy of an isolated system will increase. Hence, from one perspective, entropy measurement is a way of distinguishing the past from the future. However in thermodynamic systems that are not closed, entropy can decrease with time: many systems, including living systems
, reduce local entropy at the expense of an environmental increase, resulting in a net increase in entropy. Examples of such systems and phenomena include the formation of certain crystals, the workings of a refrigerator
and living organisms.
By contrast, all physical processes occurring at the microscopic level, such as mechanics, do not pick out an arrow of time. Going forward in time, an atom might move to the left, whereas going backward in time the same atom might move to the right; the behavior of the atom is not qualitatively different in either case. In contrast, it would be an astronomically improbable event if a macroscopic amount of gas that originally filled a container evenly spontaneously shrunk to occupy only half the container.
Certain subatomic interactions involving the weak nuclear force violate the conservation of parity, but only very rarely. According to the CPT theorem
, this means they should also be time irreversible, and so establish an arrow of time
. This, however, is neither linked to the thermodynamic arrow of time, nor has anything to do with our daily experience of time irreversibility.
allows for the entropy to remain the same regardless of the direction of time. If the entropy is constant in either direction of time, there would be no preferred direction. However, the entropy can only be a constant if the system is in the highest possible state of disorder, such as a gas that always was, and always will be, uniformly spread out in its container. The existence of a thermodynamic arrow of time implies that the system is highly ordered in one time direction only, which would by definition be the "past". Thus this law is about the boundary conditions rather than the equations of motion of our world.
Unlike most other laws of physics, the Second Law of Thermodynamics is statistical in nature, and therefore its reliability arises from the huge number of particles present in macroscopic systems. It is not impossible, in principle, for all 6 × 1023 atoms in a mole
of a gas to spontaneously migrate to one half of a container; it is only fantastically unlikely—so unlikely that no macroscopic violation of the Second Law has ever been observed. T Symmetry is the symmetry of physical laws under a time reversal transformation. Although in restricted contexts one may find this symmetry, the observable universe itself does not show symmetry under time reversal, primarily due to the second law of thermodynamics.
The thermodynamic arrow is often linked to the cosmological arrow of time, because it is ultimately about the boundary conditions of the early universe. According to the Big Bang
theory, the Universe
was initially very hot with energy distributed uniformly. For a system in which gravity is important, such as the universe, this is a low-entropy state (compared to a high-entropy state of having all matter collapsed into black hole
s, a state to which the system may eventually evolve). As the Universe grows, its temperature drops, which leaves less energy available to perform useful work in the future than was available in the past. Additionally, perturbation
s in the energy density grow (eventually forming galaxies
and star
s). Thus the Universe itself has a well-defined thermodynamic arrow of time. But this does not address the question of why the initial state of the universe was that of low entropy. If cosmic expansion were to halt and reverse due to gravity, the temperature of the Universe would once again grow hotter, but its entropy would also continue to increase due to the continued growth of perturbations and the eventual black hole
formation, until the latter stages of the Big Crunch
when entropy would be lower than now.
s, for example a dye on one side and water on the other. With no barrier between the two liquids, the random jostling of their molecule
s will result in them becoming more mixed as time passes. However, if the dye and water are mixed then one does not expect them to separate out again when left to themselves. A movie of the mixing would seem realistic when played forwards, but unrealistic when played backwards.
If the large container is observed early on in the mixing process, it might be found to be only partially mixed. It would be reasonable to conclude that, without outside intervention, the liquid reached this state because it was more ordered in the past, when there was greater separation, and will be more disordered, or mixed, in the future.
Now imagine that the experiment is repeated, this time with only a few molecules, perhaps ten, in a very small container. One can easily imagine that by watching the random jostling of the molecules it might occur — by chance alone — that the molecules became neatly segregated, with all dye molecules on one side and all water molecules on the other. That this can be expected to occur from time to time can be concluded from the fluctuation theorem
; thus it is not impossible for the molecules to segregate themselves. However, for a large numbers of molecules it is so unlikely that one would have to wait, on average, many times longer than the age of the universe for it to occur. Thus a movie that showed a large number of molecules segregating themselves as described above would appear unrealistic and one would be inclined to say that the movie was being played in reverse. See Ludwig Boltzmann#The Second Law as a law of disorder.
behind the arrow of time, entropy
, and basis of the second law of thermodynamics
derive from the following set-up, as detailed by Carnot (1824), Clapeyron (1832), and Clausius (1854):
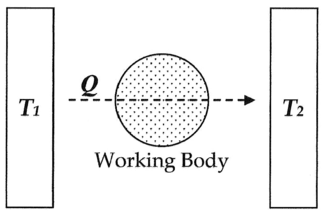
Here, as common experience demonstrates, when a hot
body T1, such as a furnace, is put into physical contact, such as being connected via a body of fluid (working body), with a cold
body T2, such as a stream of cold water, energy
will invariably flow from hot to cold in the form of heat
Q, and given time the system will reach equilibrium
. Entropy, defined as Q/T, was conceived by Rudolf Clausius
as a function to measure the molecular irreversibility
of this process, i.e. the dissipative work the atoms and molecules do on each other during the transformation.
In this diagram, one can calculate the entropy change ΔS for the passage of the quantity of heat
Q from the temperature
T1, through the "working body" of fluid (see heat engine
), which was typically a body of steam, to the temperature T2. Moreover, one could assume, for the sake of argument, that the working body contains only two molecules of water.
Next, if we make the assignment, as originally done by Clausius:
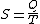
Then the entropy change or "equivalence-value" for this transformation is:
which equals:
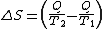
and by factoring out Q, we have the following form, as was derived by Clausius:
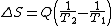
Thus, for example, if Q was 50 units, T1 was initially 100 degrees, and T2 was initially 1 degree, then the entropy change for this process would be 49.5. Hence, entropy increased for this process, the process took a certain amount of "time", and one can correlate entropy increase with the passage of time. For this system configuration, subsequently, it is an "absolute rule". This rule is based on the fact that all natural processes are irreversible
by virtue of the fact that molecules of a system, for example two molecules in a tank, will not only do external work (such as to push a piston), but will also do internal work on each other, in proportion to the heat used to do work (see: Mechanical equivalent of heat
) during the process. Entropy accounts for the fact that internal inter-molecular friction exists.
introduced a now-famous thought experiment
that highlighted the contrast between the statistical nature of entropy and the deterministic nature of the underlying physical processes. This experiment, known as Maxwell's demon
, consists of a hypothetical "demon" that guards a trapdoor between two containers filled with gases at equal temperatures. By allowing fast molecules through the trapdoor in only one direction and only slow molecules in the other direction, the demon raises the temperature of one gas and lowers the temperature of the other, apparently violating the Second Law.
Maxwell's thought experiment was only resolved in the 20th century by Leó Szilárd
, Charles H. Bennett
, Seth Lloyd
and others. The key idea is that the demon itself necessarily possesses a non-negligible amount of entropy that increases even as the gases lose entropy, so that the entropy of the system as a whole increases. This is because the demon has to contain many internal "parts" (essentially: a memory space to store information on the gas molecules) if it is to perform its job reliably, and therefore has to be considered a macroscopic system with non-vanishing entropy. An equivalent way of saying this is that the information
possessed by the demon on which atoms are considered "fast" or "slow", can be considered a form of entropy known as information entropy
.
Take for example (experiment A) a closed box which is, at the beginning, half-filled with ideal gas. As time passes, the gas obviously expands to fill the whole box, so that the final state will be a box full of gas. This is an irreversible process, since if the box is full at the beginning (experiment B), it will not become only half-full later, except for the most unlikely situation where the gas particles have very special locations and speeds. But this is precisely because we always assume that the initial conditions are such that the particles have random locations and speeds. This is not correct for the final conditions of the system, because the particles have interacted between themselves, so that their locations and speeds have become dependent on each other, i.e. correlated. This can be understood if we look at experiment A backwards in time, which we'll call experiment C: now we begin with a box full of gas, but the particles do not have random locations and speeds; rather, their locations and speeds are so particular, that after some time they all move to one half of the box, which is the final state of the system (this is the initial state of experiment A, because now we're looking at the same experiment backwards!). The interactions between particles now do not create correlations between the particles, but in fact turn them into (at least seemingly) random, "canceling" the pre-existing correlations.
The only difference between experiment C (which defies the Second Law of Thermodynamics) and experiment B (which obeys the Second Law of Thermodynamics) is that in the former the particles are uncorrelated at the end, while in the latter the particles are uncorrelated at the beginning.
In fact, if all the microscopic physical processes are reversible (see discussion below), then the Second Law of Thermodynamics can be proven for any isolated system of particles with initial conditions in which the particles states are uncorrelated. In order to do this one must acknowledge the difference between the measured entropy of a system - which is dependent only on its macrostate (its volume, temperature etc.) - and its information entropy
(also called Kolmogorov complexity
), which is the amount of information (number of computer bits) needed to describe the exact microstate
of the system. The measured entropy is independent of correlations between particles in the system, because they do not affect its macrostate, but the information entropy does depend on them, because correlations lower the randomness of the system and thus lowers the amount of information needed to describe it. Therefore, in the absence of such correlations the two entropies are identical, but otherwise the information entropy will be smaller than the measured entropy, and the difference can be used as a measure of the amount of correlations.
Now, by Liouvilles theorem, time-reversal of all microscopic processes implies that the amount of information needed to describe the exact microstate
of an isolated system (its information-theoretic joint entropy) is constant in time. This joint entropy is equal to the marginal entropy (entropy assuming no correlations) plus the entropy of correlation (mutual entropy, or its negative mutual information
). If we assume no correlations between the particles initially, then this joint entropy is just the marginal entropy which is just the initial thermodynamic entropy of the system, divided by Boltzmann's constant. However, if these are indeed the initial conditions (and this is a crucial assumption), then such correlations will form with time. In other words, there will be a decreasing mutual entropy (or increasing mutual information), and for a time which is not too long - the correlations (mutual information) between particles will only increase with time; therefore, the thermodynamic entropy , which is proportional to the marginal entropy, must also increase with time (note that "not too long" in this context is relative to the time needed, in a classical version of the system, for it to pass through all its possible microstates - a time which can be roughly estimated as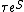
, where 
is the time between particle collisions and S is the system's entropy. In any practical case this time is huge compared to everything else). Note that the correlation between particles is not a fully objective quantity - one cannot measure the mutual entropy, one can only measure its change, assuming one can measure a microstate. Thermodynamics is restricted to the case where microstates cannot be distinguished, which means that only the marginal entropy, proportional to the thermodynamic entropy, can be measured, and, in a practical sense, always increases.
. This includes the fact that ice cubes melt in hot coffee rather than assembling themselves out of the coffee, that a block sliding on a rough surface slows down rather than speeding up, and that we can remember the past rather than the future. This last phenomenon, called the "psychological arrow of time", has deep connections with Maxwell's demon and the physics of information; In fact, it is easy to understand its link to the Second Law of Thermodynamics if one views memory as correlation between brain cells (or computer bits) and the outer world. Since the Second Law of Thermodynamics is equivalent to the growth with time of such correlations, then it states that memory will be created as we move towards the future (rather than towards the past).
boundary conditions.
, where one of the parameters is explicitly time. By the very nature of differential equations, the solutions to such systems are inherently time-reversible. However, many of the interesting cases are either ergodic or mixing
, and it is strongly suspected that mixing and ergodicity somehow underlie the fundamental mechanism of the arrow of time.
Mixing and ergodic systems do not have exact solutions, and thus proving time irreversibility in a mathematical sense is impossible. Some progress can be made by studying discrete-time models or difference equations.
Many discrete-time models, such as the iterated function
s considered in popular fractal-drawing programs, are explicitly not time-reversible, as any given point "in the present" may have several different "pasts" associated with it: indeed, the set of all pasts is known as the Julia set
. Since such systems have a built-in irreversibility, it is inappropriate to use them to explain why time is not reversible.
There are other systems which are chaotic, and are also explicitly time-reversible: among these is the baker's map
, which is also exactly solvable. An interesting avenue of study is to examine solutions to such systems not by iterating the dynamical system over time, but instead, to study the corresponding Frobenius-Perron operator or transfer operator
for the system. For some of these systems, it can be explicitly, mathematically shown that the transfer operators are not trace-class. This means that these operators do not have a unique eigenvalue spectrum that is independent of the choice of basis. In the case of the baker's map, it can be shown that several unique and inequivalent diagonalizations or bases exist, each with a different set of eigenvalues. It is this phenomenon that can be offered as an "explanation" for the arrow of time. That is, although the iterated, discrete-time system is explicitly time-symmetric, the transfer operator is not. Furthermore, the transfer operator can be diagonalized in one of two inequivalent ways, one of which describes the forward-time evolution of the system, and one which describes the backwards-time evolution.
As of 2006, this type of time-symmetry breaking has been demonstrated for only a very small number of exactly-solvable, discrete-time systems. The transfer operator for more complex systems has not been consistently formulated, and its precise definition is mired in a variety of subtle difficulties. In particular, it has not been shown that it has a broken symmetry for the simplest exactly-solvable continuous-time ergodic systems, such as Hadamard's billiards, or the Anosov flow on the tangent space of PSL(2,R).
s, and in particular, how discrete and continuous eigenvalue spectra intermingle. For example, the rational number
s are completely intermingled with the real number
s, and yet have a unique, distinct set of properties. It is hoped that the study of Hilbert spaces with a similar inter-mingling will provide insight into the arrow of time.
Another distinct approach is through the study of quantum chaos
by which attempts are made to quantize systems as classically chaotic, ergodic or mixing. The results obtained are not dissimilar from those that come from the transfer operator method. For example, the quantization of the Boltzmann gas, that is, a gas of hard (elastic) point particles in a rectangular box reveals that the eigenfunctions are space-filling fractals that occupy the entire box, and that the energy eigenvalues are very closely spaced and have an "almost continuous" spectrum (for a finite number of particles in a box, the spectrum must be, of necessity, discrete). If the initial conditions are such that all of the particles are confined to one side of the box, the system very quickly evolves into one where the particles fill the entire box. Even when all of the particles are initially on one side of the box, their wave functions do, in fact, permeate the entire box: they constructively interfere on one side, and destructively interfere on the other. Irreversibility is then argued by noting that it is "nearly impossible" for the wave functions to be "accidentally" arranged in some unlikely state: such arrangements are a set of zero measure
. Because the eigenfunctions are fractals, much of the language and machinery of entropy and statistical mechanics can be imported to discuss and argue the quantum case.
), and are therefore unrelated to the second law of thermodynamics
, or to our day-to-day experience of the arrow of time. A notable exception is the wave function collapse in quantum mechanics
, which is an irreversible process. It has been conjectured that the collapse of the wave function may be the reason for the Second Law of Thermodynamics. However it is more accepted today that the opposite is correct, namely that the (possibly merely apparent) wave function collapse is a consequence of quantum decoherence
, a process which is ultimately an outcome of the Second Law of Thermodynamics.
It currently seems that the ultimate reason for a preferred time direction is that the universe
as a whole was in a highly ordered state at its very early stages, shortly after the big bang
, and that any fluctuations in it were uncorrelated. The question of why this highly ordered state existed, and how to describe it, remains an area of research. Currently, the most promising direction is the theory of cosmic inflation
.
According to this theory our universe (or, rather, its accessible part, a radius of 46 billion light years around our location) evolved from a tiny, totally uniform volume (a portion of a much bigger universe), which expanded greatly; hence it was highly ordered. Fluctuations were then created by quantum processes related to its expansion, in a manner which is supposed to be such that these fluctuations are uncorrelated for any practical use. This is supposed to give the desired initial conditions needed for the Second Law of Thermodynamics.
Our universe is probably an open universe, so that its expansion will never terminate, but it is an interesting thought experiment
to imagine what would have happened had our universe been closed. In such a case, its expansion will stop at a certain time in the distant future, and it will then begin to shrink. Moreover, a closed universe is finite.
It is unclear what will happen to the Second Law of Thermodynamics
in such a case. One could imagine at least three different scenarios (in fact, only the third one is probable, since the first two require very simple cosmic evolution):
In the first scenario, the cosmological arrow of time
is the reason for both the thermodynamic arrow of time and the quantum arrow of time. Both will slowly disappear as the universe will come to a halt, and will later be reversed.
In the second and third scenarios, it is the difference between the initial state and the final state of the universe that is responsible for the thermodynamic arrow of time. This is independent of the cosmological arrow of time. In the second scenario, the quantum arrow of time may be seen as the deep reason for this.
Dover has reprinted the monograph in 2003 (ISBN 0486432432). For a short paper listing “the essential points of that argument, correcting presentation points that were confusing ... and emphasizing conclusions more forcefully than previously” see
Arrow of time
The arrow of time, or time’s arrow, is a term coined in 1927 by the British astronomer Arthur Eddington to describe the "one-way direction" or "asymmetry" of time...
. As one goes "forward" in time, the second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
says, the entropy of an isolated system will increase. Hence, from one perspective, entropy measurement is a way of distinguishing the past from the future. However in thermodynamic systems that are not closed, entropy can decrease with time: many systems, including living systems
Entropy and life
Research concerning the relationship between the thermodynamic quantity entropy and the evolution of life began in around the turn of the 20th century...
, reduce local entropy at the expense of an environmental increase, resulting in a net increase in entropy. Examples of such systems and phenomena include the formation of certain crystals, the workings of a refrigerator
Refrigerator
A refrigerator is a common household appliance that consists of a thermally insulated compartment and a heat pump that transfers heat from the inside of the fridge to its external environment so that the inside of the fridge is cooled to a temperature below the ambient temperature of the room...
and living organisms.
By contrast, all physical processes occurring at the microscopic level, such as mechanics, do not pick out an arrow of time. Going forward in time, an atom might move to the left, whereas going backward in time the same atom might move to the right; the behavior of the atom is not qualitatively different in either case. In contrast, it would be an astronomically improbable event if a macroscopic amount of gas that originally filled a container evenly spontaneously shrunk to occupy only half the container.
Certain subatomic interactions involving the weak nuclear force violate the conservation of parity, but only very rarely. According to the CPT theorem
CPT symmetry
CPT symmetry is a fundamental symmetry of physical laws under transformations that involve the inversions of charge, parity, and time simultaneously.-History:...
, this means they should also be time irreversible, and so establish an arrow of time
Arrow of time
The arrow of time, or time’s arrow, is a term coined in 1927 by the British astronomer Arthur Eddington to describe the "one-way direction" or "asymmetry" of time...
. This, however, is neither linked to the thermodynamic arrow of time, nor has anything to do with our daily experience of time irreversibility.
Overview
The Second Law of ThermodynamicsSecond law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
allows for the entropy to remain the same regardless of the direction of time. If the entropy is constant in either direction of time, there would be no preferred direction. However, the entropy can only be a constant if the system is in the highest possible state of disorder, such as a gas that always was, and always will be, uniformly spread out in its container. The existence of a thermodynamic arrow of time implies that the system is highly ordered in one time direction only, which would by definition be the "past". Thus this law is about the boundary conditions rather than the equations of motion of our world.
Unlike most other laws of physics, the Second Law of Thermodynamics is statistical in nature, and therefore its reliability arises from the huge number of particles present in macroscopic systems. It is not impossible, in principle, for all 6 × 1023 atoms in a mole
Mole (unit)
The mole is a unit of measurement used in chemistry to express amounts of a chemical substance, defined as an amount of a substance that contains as many elementary entities as there are atoms in 12 grams of pure carbon-12 , the isotope of carbon with atomic weight 12. This corresponds to a value...
of a gas to spontaneously migrate to one half of a container; it is only fantastically unlikely—so unlikely that no macroscopic violation of the Second Law has ever been observed. T Symmetry is the symmetry of physical laws under a time reversal transformation. Although in restricted contexts one may find this symmetry, the observable universe itself does not show symmetry under time reversal, primarily due to the second law of thermodynamics.
The thermodynamic arrow is often linked to the cosmological arrow of time, because it is ultimately about the boundary conditions of the early universe. According to the Big Bang
Big Bang
The Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
theory, the Universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
was initially very hot with energy distributed uniformly. For a system in which gravity is important, such as the universe, this is a low-entropy state (compared to a high-entropy state of having all matter collapsed into black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
s, a state to which the system may eventually evolve). As the Universe grows, its temperature drops, which leaves less energy available to perform useful work in the future than was available in the past. Additionally, perturbation
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
s in the energy density grow (eventually forming galaxies
Galaxy
A galaxy is a massive, gravitationally bound system that consists of stars and stellar remnants, an interstellar medium of gas and dust, and an important but poorly understood component tentatively dubbed dark matter. The word galaxy is derived from the Greek galaxias , literally "milky", a...
and star
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
s). Thus the Universe itself has a well-defined thermodynamic arrow of time. But this does not address the question of why the initial state of the universe was that of low entropy. If cosmic expansion were to halt and reverse due to gravity, the temperature of the Universe would once again grow hotter, but its entropy would also continue to increase due to the continued growth of perturbations and the eventual black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
formation, until the latter stages of the Big Crunch
Big Crunch
In physical cosmology, the Big Crunch is one possible scenario for the ultimate fate of the universe, in which the metric expansion of space eventually reverses and the universe recollapses, ultimately ending as a black hole singularity.- Overview :...
when entropy would be lower than now.
An example of apparent irreversibility
Consider the situation in which a large container is filled with two separated liquidLiquid
Liquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...
s, for example a dye on one side and water on the other. With no barrier between the two liquids, the random jostling of their molecule
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
s will result in them becoming more mixed as time passes. However, if the dye and water are mixed then one does not expect them to separate out again when left to themselves. A movie of the mixing would seem realistic when played forwards, but unrealistic when played backwards.
If the large container is observed early on in the mixing process, it might be found to be only partially mixed. It would be reasonable to conclude that, without outside intervention, the liquid reached this state because it was more ordered in the past, when there was greater separation, and will be more disordered, or mixed, in the future.
Now imagine that the experiment is repeated, this time with only a few molecules, perhaps ten, in a very small container. One can easily imagine that by watching the random jostling of the molecules it might occur — by chance alone — that the molecules became neatly segregated, with all dye molecules on one side and all water molecules on the other. That this can be expected to occur from time to time can be concluded from the fluctuation theorem
Fluctuation theorem
The fluctuation theorem , which originated from statistical mechanics, deals with the relative probability that the entropy of a system which is currently away from thermodynamic equilibrium will increase or decrease over a given amount of time...
; thus it is not impossible for the molecules to segregate themselves. However, for a large numbers of molecules it is so unlikely that one would have to wait, on average, many times longer than the age of the universe for it to occur. Thus a movie that showed a large number of molecules segregating themselves as described above would appear unrealistic and one would be inclined to say that the movie was being played in reverse. See Ludwig Boltzmann#The Second Law as a law of disorder.
Mathematics of the arrow
The mathematicsMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
behind the arrow of time, entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
, and basis of the second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
derive from the following set-up, as detailed by Carnot (1824), Clapeyron (1832), and Clausius (1854):
Here, as common experience demonstrates, when a hot
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
body T1, such as a furnace, is put into physical contact, such as being connected via a body of fluid (working body), with a cold
Cold
Cold describes the condition of low temperature.Cold may also refer to:*Common cold, a contagious viral infectious disease of the upper respiratory system*Chronic obstructive pulmonary disease...
body T2, such as a stream of cold water, energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
will invariably flow from hot to cold in the form of heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
Q, and given time the system will reach equilibrium
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
. Entropy, defined as Q/T, was conceived by Rudolf Clausius
Rudolf Clausius
Rudolf Julius Emanuel Clausius , was a German physicist and mathematician and is considered one of the central founders of the science of thermodynamics. By his restatement of Sadi Carnot's principle known as the Carnot cycle, he put the theory of heat on a truer and sounder basis...
as a function to measure the molecular irreversibility
Irreversibility
In science, a process that is not reversible is called irreversible. This concept arises most frequently in thermodynamics, as applied to processes....
of this process, i.e. the dissipative work the atoms and molecules do on each other during the transformation.
In this diagram, one can calculate the entropy change ΔS for the passage of the quantity of heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
Q from the temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
T1, through the "working body" of fluid (see heat engine
Heat engine
In thermodynamics, a heat engine is a system that performs the conversion of heat or thermal energy to mechanical work. It does this by bringing a working substance from a high temperature state to a lower temperature state. A heat "source" generates thermal energy that brings the working substance...
), which was typically a body of steam, to the temperature T2. Moreover, one could assume, for the sake of argument, that the working body contains only two molecules of water.
Next, if we make the assignment, as originally done by Clausius:
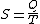
Then the entropy change or "equivalence-value" for this transformation is:
which equals:
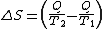
and by factoring out Q, we have the following form, as was derived by Clausius:
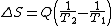
Thus, for example, if Q was 50 units, T1 was initially 100 degrees, and T2 was initially 1 degree, then the entropy change for this process would be 49.5. Hence, entropy increased for this process, the process took a certain amount of "time", and one can correlate entropy increase with the passage of time. For this system configuration, subsequently, it is an "absolute rule". This rule is based on the fact that all natural processes are irreversible
Irreversible
Irreversible may refer to:*Irreversible process, in thermodynamics, a process that is not reversible*Irréversible, a 2002 film*Irréversible , soundtrack to the film Irréversible...
by virtue of the fact that molecules of a system, for example two molecules in a tank, will not only do external work (such as to push a piston), but will also do internal work on each other, in proportion to the heat used to do work (see: Mechanical equivalent of heat
Mechanical equivalent of heat
In the history of science, the mechanical equivalent of heat was a concept that had an important part in the development and acceptance of the conservation of energy and the establishment of the science of thermodynamics in the 19th century....
) during the process. Entropy accounts for the fact that internal inter-molecular friction exists.
Maxwell's demon
In 1867, James Clerk MaxwellJames Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
introduced a now-famous thought experiment
Thought experiment
A thought experiment or Gedankenexperiment considers some hypothesis, theory, or principle for the purpose of thinking through its consequences...
that highlighted the contrast between the statistical nature of entropy and the deterministic nature of the underlying physical processes. This experiment, known as Maxwell's demon
Maxwell's demon
In the philosophy of thermal and statistical physics, Maxwell's demon is a thought experiment created by the Scottish physicist James Clerk Maxwell to "show that the Second Law of Thermodynamics has only a statistical certainty." It demonstrates Maxwell's point by hypothetically describing how to...
, consists of a hypothetical "demon" that guards a trapdoor between two containers filled with gases at equal temperatures. By allowing fast molecules through the trapdoor in only one direction and only slow molecules in the other direction, the demon raises the temperature of one gas and lowers the temperature of the other, apparently violating the Second Law.
Maxwell's thought experiment was only resolved in the 20th century by Leó Szilárd
Leó Szilárd
Leó Szilárd was an Austro-Hungarian physicist and inventor who conceived the nuclear chain reaction in 1933, patented the idea of a nuclear reactor with Enrico Fermi, and in late 1939 wrote the letter for Albert Einstein's signature that resulted in the Manhattan Project that built the atomic bomb...
, Charles H. Bennett
Charles H. Bennett (computer scientist)
Charles H. Bennett is an IBM Fellow at IBM Research. Bennett's recent work at IBM has concentrated on a re-examination of the physical basis of information, applying quantum physics to the problems surrounding information exchange...
, Seth Lloyd
Seth Lloyd
Seth Lloyd is a professor of mechanical engineering at the Massachusetts Institute of Technology. He refers to himself as a "quantum mechanic"....
and others. The key idea is that the demon itself necessarily possesses a non-negligible amount of entropy that increases even as the gases lose entropy, so that the entropy of the system as a whole increases. This is because the demon has to contain many internal "parts" (essentially: a memory space to store information on the gas molecules) if it is to perform its job reliably, and therefore has to be considered a macroscopic system with non-vanishing entropy. An equivalent way of saying this is that the information
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
possessed by the demon on which atoms are considered "fast" or "slow", can be considered a form of entropy known as information entropy
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
.
Correlations
An important difference between the past and the future is that in any system (such as a gas of particles) its initial conditions are usually such that its different parts are uncorrelated, but as the system evolves and its different parts interact with each other, they become correlated. For example, whenever dealing with a gas of particles, it is always assumed that its initial conditions are such that there is no correlation between the states of different particles (i.e. the speeds and locations of the different particles are completely random, up to the need to conform with the macrostate of the system). This is closely related to the Second Law of Thermodynamics.Take for example (experiment A) a closed box which is, at the beginning, half-filled with ideal gas. As time passes, the gas obviously expands to fill the whole box, so that the final state will be a box full of gas. This is an irreversible process, since if the box is full at the beginning (experiment B), it will not become only half-full later, except for the most unlikely situation where the gas particles have very special locations and speeds. But this is precisely because we always assume that the initial conditions are such that the particles have random locations and speeds. This is not correct for the final conditions of the system, because the particles have interacted between themselves, so that their locations and speeds have become dependent on each other, i.e. correlated. This can be understood if we look at experiment A backwards in time, which we'll call experiment C: now we begin with a box full of gas, but the particles do not have random locations and speeds; rather, their locations and speeds are so particular, that after some time they all move to one half of the box, which is the final state of the system (this is the initial state of experiment A, because now we're looking at the same experiment backwards!). The interactions between particles now do not create correlations between the particles, but in fact turn them into (at least seemingly) random, "canceling" the pre-existing correlations.
The only difference between experiment C (which defies the Second Law of Thermodynamics) and experiment B (which obeys the Second Law of Thermodynamics) is that in the former the particles are uncorrelated at the end, while in the latter the particles are uncorrelated at the beginning.
In fact, if all the microscopic physical processes are reversible (see discussion below), then the Second Law of Thermodynamics can be proven for any isolated system of particles with initial conditions in which the particles states are uncorrelated. In order to do this one must acknowledge the difference between the measured entropy of a system - which is dependent only on its macrostate (its volume, temperature etc.) - and its information entropy
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
(also called Kolmogorov complexity
Kolmogorov complexity
In algorithmic information theory , the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computational resources needed to specify the object...
), which is the amount of information (number of computer bits) needed to describe the exact microstate
Microstate (statistical mechanics)
In statistical mechanics, a microstate is a specific microscopic configuration of a thermodynamic system that the system may occupy with a certain probability in the course of its thermal fluctuations...
of the system. The measured entropy is independent of correlations between particles in the system, because they do not affect its macrostate, but the information entropy does depend on them, because correlations lower the randomness of the system and thus lowers the amount of information needed to describe it. Therefore, in the absence of such correlations the two entropies are identical, but otherwise the information entropy will be smaller than the measured entropy, and the difference can be used as a measure of the amount of correlations.
Now, by Liouvilles theorem, time-reversal of all microscopic processes implies that the amount of information needed to describe the exact microstate
Microstate (statistical mechanics)
In statistical mechanics, a microstate is a specific microscopic configuration of a thermodynamic system that the system may occupy with a certain probability in the course of its thermal fluctuations...
of an isolated system (its information-theoretic joint entropy) is constant in time. This joint entropy is equal to the marginal entropy (entropy assuming no correlations) plus the entropy of correlation (mutual entropy, or its negative mutual information
Mutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
). If we assume no correlations between the particles initially, then this joint entropy is just the marginal entropy which is just the initial thermodynamic entropy of the system, divided by Boltzmann's constant. However, if these are indeed the initial conditions (and this is a crucial assumption), then such correlations will form with time. In other words, there will be a decreasing mutual entropy (or increasing mutual information), and for a time which is not too long - the correlations (mutual information) between particles will only increase with time; therefore, the thermodynamic entropy , which is proportional to the marginal entropy, must also increase with time (note that "not too long" in this context is relative to the time needed, in a classical version of the system, for it to pass through all its possible microstates - a time which can be roughly estimated as
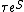, where is the time between particle collisions and S is the system's entropy. In any practical case this time is huge compared to everything else). Note that the correlation between particles is not a fully objective quantity - one cannot measure the mutual entropy, one can only measure its change, assuming one can measure a microstate. Thermodynamics is restricted to the case where microstates cannot be distinguished, which means that only the marginal entropy, proportional to the thermodynamic entropy, can be measured, and, in a practical sense, always increases.The arrow of time in various phenomena
All phenomena that behave differently in one time direction can ultimately be linked to the Second Law of ThermodynamicsSecond law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
. This includes the fact that ice cubes melt in hot coffee rather than assembling themselves out of the coffee, that a block sliding on a rough surface slows down rather than speeding up, and that we can remember the past rather than the future. This last phenomenon, called the "psychological arrow of time", has deep connections with Maxwell's demon and the physics of information; In fact, it is easy to understand its link to the Second Law of Thermodynamics if one views memory as correlation between brain cells (or computer bits) and the outer world. Since the Second Law of Thermodynamics is equivalent to the growth with time of such correlations, then it states that memory will be created as we move towards the future (rather than towards the past).
Current research
Current research focuses mainly on describing the thermodynamic arrow of time mathematically, either in classical or quantum systems, and on understanding its origin from the point of view of cosmologicalCosmology
Cosmology is the discipline that deals with the nature of the Universe as a whole. Cosmologists seek to understand the origin, evolution, structure, and ultimate fate of the Universe at large, as well as the natural laws that keep it in order...
boundary conditions.
Dynamical systems
Some current research in dynamical systems indicates a possible "explanation" for the arrow of time. There are several ways to describe the time evolution of a dynamical system. In the classical framework, one considers a differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
, where one of the parameters is explicitly time. By the very nature of differential equations, the solutions to such systems are inherently time-reversible. However, many of the interesting cases are either ergodic or mixing
Mixing (physics)
In physics, a dynamical system is said to be mixing if the phase space of the system becomes strongly intertwined, according to at least one of several mathematical definitions. For example, a measure-preserving transformation T is said to be strong mixing ifwhenever A and B are any measurable...
, and it is strongly suspected that mixing and ergodicity somehow underlie the fundamental mechanism of the arrow of time.
Mixing and ergodic systems do not have exact solutions, and thus proving time irreversibility in a mathematical sense is impossible. Some progress can be made by studying discrete-time models or difference equations.
Many discrete-time models, such as the iterated function
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
s considered in popular fractal-drawing programs, are explicitly not time-reversible, as any given point "in the present" may have several different "pasts" associated with it: indeed, the set of all pasts is known as the Julia set
Julia set
In the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
. Since such systems have a built-in irreversibility, it is inappropriate to use them to explain why time is not reversible.
There are other systems which are chaotic, and are also explicitly time-reversible: among these is the baker's map
Baker's map
In dynamical systems theory, the baker's map is a chaotic map from the unit square into itself. It is named after a kneading operation that bakers apply to dough: the dough is cut in half, and the two halves are stacked on one-another, and compressed...
, which is also exactly solvable. An interesting avenue of study is to examine solutions to such systems not by iterating the dynamical system over time, but instead, to study the corresponding Frobenius-Perron operator or transfer operator
Transfer operator
In mathematics, the transfer operator encodes information about an iterated map and is frequently used to study the behavior of dynamical systems, statistical mechanics, quantum chaos and fractals...
for the system. For some of these systems, it can be explicitly, mathematically shown that the transfer operators are not trace-class. This means that these operators do not have a unique eigenvalue spectrum that is independent of the choice of basis. In the case of the baker's map, it can be shown that several unique and inequivalent diagonalizations or bases exist, each with a different set of eigenvalues. It is this phenomenon that can be offered as an "explanation" for the arrow of time. That is, although the iterated, discrete-time system is explicitly time-symmetric, the transfer operator is not. Furthermore, the transfer operator can be diagonalized in one of two inequivalent ways, one of which describes the forward-time evolution of the system, and one which describes the backwards-time evolution.
As of 2006, this type of time-symmetry breaking has been demonstrated for only a very small number of exactly-solvable, discrete-time systems. The transfer operator for more complex systems has not been consistently formulated, and its precise definition is mired in a variety of subtle difficulties. In particular, it has not been shown that it has a broken symmetry for the simplest exactly-solvable continuous-time ergodic systems, such as Hadamard's billiards, or the Anosov flow on the tangent space of PSL(2,R).
Quantum mechanics
Research on irreversibility in quantum mechanics takes several different directions. One avenue is the study of rigged Hilbert spaceRigged Hilbert space
In mathematics, a rigged Hilbert space is a construction designed to link the distribution and square-integrable aspects of functional analysis. Such spaces were introduced to study spectral theory in the broad sense...
s, and in particular, how discrete and continuous eigenvalue spectra intermingle. For example, the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s are completely intermingled with the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, and yet have a unique, distinct set of properties. It is hoped that the study of Hilbert spaces with a similar inter-mingling will provide insight into the arrow of time.
Another distinct approach is through the study of quantum chaos
Quantum chaos
Quantum chaos is a branch of physics which studies how chaotic classical dynamical systems can be described in terms of quantum theory. The primary question that quantum chaos seeks to answer is, "What is the relationship between quantum mechanics and classical chaos?" The correspondence principle...
by which attempts are made to quantize systems as classically chaotic, ergodic or mixing. The results obtained are not dissimilar from those that come from the transfer operator method. For example, the quantization of the Boltzmann gas, that is, a gas of hard (elastic) point particles in a rectangular box reveals that the eigenfunctions are space-filling fractals that occupy the entire box, and that the energy eigenvalues are very closely spaced and have an "almost continuous" spectrum (for a finite number of particles in a box, the spectrum must be, of necessity, discrete). If the initial conditions are such that all of the particles are confined to one side of the box, the system very quickly evolves into one where the particles fill the entire box. Even when all of the particles are initially on one side of the box, their wave functions do, in fact, permeate the entire box: they constructively interfere on one side, and destructively interfere on the other. Irreversibility is then argued by noting that it is "nearly impossible" for the wave functions to be "accidentally" arranged in some unlikely state: such arrangements are a set of zero measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
. Because the eigenfunctions are fractals, much of the language and machinery of entropy and statistical mechanics can be imported to discuss and argue the quantum case.
Cosmology
Some processes which involve high energy particles and are governed by the weak force (such as K-meson decay) defy the symmetry between time directions. However, all known physical processes do preserve a more complicated symmetry (CPT symmetryCPT symmetry
CPT symmetry is a fundamental symmetry of physical laws under transformations that involve the inversions of charge, parity, and time simultaneously.-History:...
), and are therefore unrelated to the second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
, or to our day-to-day experience of the arrow of time. A notable exception is the wave function collapse in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, which is an irreversible process. It has been conjectured that the collapse of the wave function may be the reason for the Second Law of Thermodynamics. However it is more accepted today that the opposite is correct, namely that the (possibly merely apparent) wave function collapse is a consequence of quantum decoherence
Quantum decoherence
In quantum mechanics, quantum decoherence is the loss of coherence or ordering of the phase angles between the components of a system in a quantum superposition. A consequence of this dephasing leads to classical or probabilistically additive behavior...
, a process which is ultimately an outcome of the Second Law of Thermodynamics.
It currently seems that the ultimate reason for a preferred time direction is that the universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
as a whole was in a highly ordered state at its very early stages, shortly after the big bang
Big Bang
The Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
, and that any fluctuations in it were uncorrelated. The question of why this highly ordered state existed, and how to describe it, remains an area of research. Currently, the most promising direction is the theory of cosmic inflation
Cosmic inflation
In physical cosmology, cosmic inflation, cosmological inflation or just inflation is the theorized extremely rapid exponential expansion of the early universe by a factor of at least 1078 in volume, driven by a negative-pressure vacuum energy density. The inflationary epoch comprises the first part...
.
According to this theory our universe (or, rather, its accessible part, a radius of 46 billion light years around our location) evolved from a tiny, totally uniform volume (a portion of a much bigger universe), which expanded greatly; hence it was highly ordered. Fluctuations were then created by quantum processes related to its expansion, in a manner which is supposed to be such that these fluctuations are uncorrelated for any practical use. This is supposed to give the desired initial conditions needed for the Second Law of Thermodynamics.
Our universe is probably an open universe, so that its expansion will never terminate, but it is an interesting thought experiment
Thought experiment
A thought experiment or Gedankenexperiment considers some hypothesis, theory, or principle for the purpose of thinking through its consequences...
to imagine what would have happened had our universe been closed. In such a case, its expansion will stop at a certain time in the distant future, and it will then begin to shrink. Moreover, a closed universe is finite.
It is unclear what will happen to the Second Law of Thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
in such a case. One could imagine at least three different scenarios (in fact, only the third one is probable, since the first two require very simple cosmic evolution):
- A highly controversial view is that in such a case the arrow of time will be reversed. The quantum fluctuations - which in the meantime have evolved into galaxies and stars - will be in superpositionSuperposition principleIn physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
in such a way that the whole process described above is reversed - i.e. the fluctuations are erased by destructive interference and total uniformity is achieved once again. Thus the universe ends in a big crunchBig CrunchIn physical cosmology, the Big Crunch is one possible scenario for the ultimate fate of the universe, in which the metric expansion of space eventually reverses and the universe recollapses, ultimately ending as a black hole singularity.- Overview :...
which is very similar to its beginning in the big bangBig BangThe Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
. Because the two are totally symmetric, and the final state is very highly ordered - entropy has to decrease close to the end of the universe, so that the Second Law of Thermodynamics is reversed when the universe shrinks. This can be understood as follows: in the very early universe, interactions between fluctuations created entanglementEntanglementEntanglement may refer to:* Quantum entanglement* Orientation entanglement* Entanglement * Entanglement of polymer chains, see Reptation* Wire entanglement...
(quantum correlationQuantum correlationIn Bell test experiments the term quantum correlation has come to mean the expectation value of the product of the outcomes on the two sides. In other words, the expected change in physical characteristics as one quantum system passes through an interaction site...
s) between particles spread all over the universe; during the expansion, these particles became so distant that these correlations became negligible (see quantum decoherenceQuantum decoherenceIn quantum mechanics, quantum decoherence is the loss of coherence or ordering of the phase angles between the components of a system in a quantum superposition. A consequence of this dephasing leads to classical or probabilistically additive behavior...
). At the time the expansion halts and the universe starts to shrink, such correlated particles arrive once again at contact (after circling around the universe), and the entropy starts to decrease - because highly correlated initial conditions may lead to a decrease in entropy. Another way of putting it, is that as distant particles arrive, more and more order is revealed because these particles are highly correlated with particles which have arrived earlier.
- It could be that this is the crucial point where the wavefunction collapseWavefunction collapseIn quantum mechanics, wave function collapse is the phenomenon in which a wave function—initially in a superposition of several different possible eigenstates—appears to reduce to a single one of those states after interaction with an observer...
is important: if the collapse is real, then the quantum fluctuations will not be in superposition any longer; rather they had collapsed to a particular state (a particular arrangement of galaxies and stars), thus creating a big crunchBig CrunchIn physical cosmology, the Big Crunch is one possible scenario for the ultimate fate of the universe, in which the metric expansion of space eventually reverses and the universe recollapses, ultimately ending as a black hole singularity.- Overview :...
which is very different from the big bangBig BangThe Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
. Such a scenario may be viewed as adding boundary conditions (say, at the distant future) which dictate the wavefunction collapse.
- The broad consensus among the scientific community today is that smooth initial conditions lead to a highly non-smooth final state, and that this is in fact the source of the thermodynamic arrow of time. Highly non-smooth gravitational systems tend to collapse to black holeBlack holeA black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
s, so the wavefunctionWavefunctionNot to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
of the whole universe evolves from a superpositionSuperposition principleIn physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
of small fluctuations to a superpositionSuperposition principleIn physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
of states with many black holeBlack holeA black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
s in each. It may even be that it is impossible for the universe to have both a smooth beginning and a smooth ending. Note that in this scenario the energy density of the universe in the final stages of its shrinkage is much larger than in the corresponding initial stages of its expansion (there is no destructive interference, unlike in the first scenario described above), and consists of mostly black holes rather than free particles.
In the first scenario, the cosmological arrow of time
Arrow of time
The arrow of time, or time’s arrow, is a term coined in 1927 by the British astronomer Arthur Eddington to describe the "one-way direction" or "asymmetry" of time...
is the reason for both the thermodynamic arrow of time and the quantum arrow of time. Both will slowly disappear as the universe will come to a halt, and will later be reversed.
In the second and third scenarios, it is the difference between the initial state and the final state of the universe that is responsible for the thermodynamic arrow of time. This is independent of the cosmological arrow of time. In the second scenario, the quantum arrow of time may be seen as the deep reason for this.
See also
- EntropyEntropyEntropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
- History of entropyHistory of entropyThe concept of entropy developed in response to the observation that a certain amount of functional energy released from combustion reactions is always lost to dissipation or friction and is thus not transformed into useful work...
- Arrow of timeArrow of timeThe arrow of time, or time’s arrow, is a term coined in 1927 by the British astronomer Arthur Eddington to describe the "one-way direction" or "asymmetry" of time...
- Cosmic inflationCosmic inflationIn physical cosmology, cosmic inflation, cosmological inflation or just inflation is the theorized extremely rapid exponential expansion of the early universe by a factor of at least 1078 in volume, driven by a negative-pressure vacuum energy density. The inflationary epoch comprises the first part...
- H-theoremH-theoremIn Classical Statistical Mechanics, the H-theorem, introduced by Ludwig Boltzmann in 1872, describes the increase in the entropy of an ideal gas in an irreversible process. H-theorem follows from considerations of Boltzmann's equation...
- Loschmidt's paradoxLoschmidt's paradoxLoschmidt's paradox, also known as the reversibility paradox, is the objection that it should not be possible to deduce an irreversible process from time-symmetric dynamics...
Further reading
(technical).Dover has reprinted the monograph in 2003 (ISBN 0486432432). For a short paper listing “the essential points of that argument, correcting presentation points that were confusing ... and emphasizing conclusions more forcefully than previously” see
External links
- Arrow of time Eschatopaedia
- Thermodynamic Asymmetry in Time at the online Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
- Java applets simulating irreversible processes: Release of a gas from a container and Mixing of two gases